1. 引言
本文我们主要研究Banach空间E中P-Laplacian算子的分数阶微分方程边值问题:
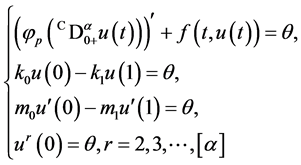 (1)
(1)
其中 ,
,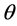 是E中的零元,
是E中的零元,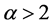 是实数,
是实数,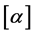 记作实数
记作实数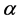 的整数部分,
的整数部分,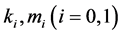 是常数满足
是常数满足 ,
,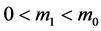 ,
, 是P-Laplacian算子,即:
是P-Laplacian算子,即: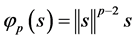 ,
,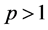 ,
, ,其中
,其中 ,
,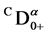 是Caputo导数,
是Caputo导数,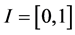 ,
, 是连续的。
是连续的。
多孔介质中的湍流是一个基本力学问题,为研究此类问题,Leibenson引入了下列带有P-Laplacian算子的微分方程:
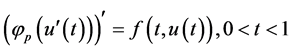 . (2)
. (2)
对微分方程(2)的研究具有非常重要的理论和实际意义,因此受到了广大学者的广泛关注,得到了许多有关微分方程在具有不同边值条件下的显著结果(见文献 [1] [2] [3] [4] )。随着研究的深入,人们开始关注非整数阶微分方程的边值问题,但是有关带有P-Laplacian算子的分数阶微分方程边值问题的研究结果还是很少的。
2010年,文献 [5] 研究了下列带有P-Laplacian算子的分数阶微分方程边值问题:
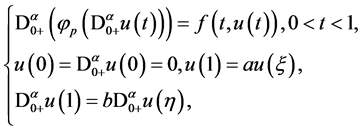
其中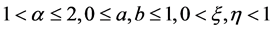 ,利用上下解的方法,作者得到了至少一个正解的存在性结果。
,利用上下解的方法,作者得到了至少一个正解的存在性结果。
2013年,文献 [6] 研究了下列带有P-Laplacian算子的分数阶微分方程边值问题:
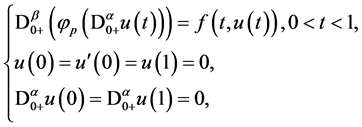
其中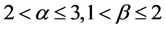 。由格林函数的性质及Guo-Krasnosel’Skii不动点定理,得到了正解的存在性及多重性的结果。
。由格林函数的性质及Guo-Krasnosel’Skii不动点定理,得到了正解的存在性及多重性的结果。
受以上文章启发,本文主要研究分数阶微分方程边值问题(1)解的存在性。与以往研究成果相比,本文我们所考虑的边值问题具有以下创新点。第一,我们是在Banach空间中研究边值问题(1)解的存在性。第二,本文中使用的主要工具是Kuratowski非紧性测度的性质和Sadovskii不动点定理,得到了解的存在性结果。最后,我们研究的微分方程带有P-Laplacian算子,特别是在Banach空间中,此类问题的研究成果尚不多见,因此研究边值问题(1)解的存在性是必要的。
2. 预备知识及主要引理
首先定义以下空间:
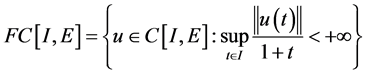 ,
,
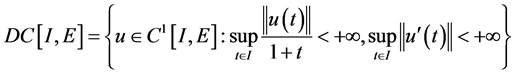 .
.
易见,空间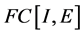 和
和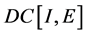 分别赋予范数
分别赋予范数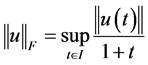 ,
,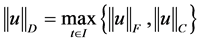 时,是Banach空间,其中
时,是Banach空间,其中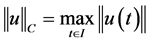 。
。
本文的基本空间是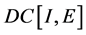 。
。
下面给出本文用到的一些概念和引理。
定义1 [7] 函数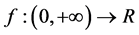 的
的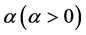 阶Captuto导数定义为:
阶Captuto导数定义为:
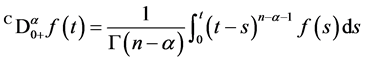 ,
,
其中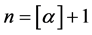 ,
,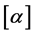 是实数
是实数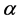 的整数部分,右端在
的整数部分,右端在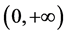 上是逐点定义的。
上是逐点定义的。
定义2 [8] (Kuratowski非紧性测度)令E是实Banach空间,S是E中的有界集,称
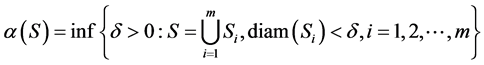
为集合S的非紧性测度,其中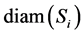 是
是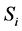 的直径。显然
的直径。显然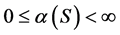 。
。
对Banach空间E中的任意有界集D,记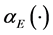 为E的Kuratowski非紧性测度。下面分别记空间
为E的Kuratowski非紧性测度。下面分别记空间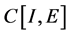 、
、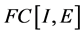 、
、 中的有界集的Kuratowski非紧性测度记作
中的有界集的Kuratowski非紧性测度记作 、
、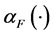 和
和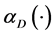 。
。
定义3 [8] 令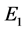 和
和 是实Banach空间,
是实Banach空间,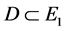 ,
,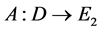 是连续有界的算子,
是连续有界的算子,
1) 如果存在常数 ,对E中的任意有界集S,使得
,对E中的任意有界集S,使得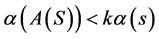 ,则称A是k-集压缩映像。当
,则称A是k-集压缩映像。当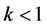 时,则称A为严格集压缩映像。
时,则称A为严格集压缩映像。
2) 如果对E中任意非相对紧的有界集S,有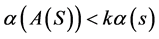 ,则称A是凝聚映像。
,则称A是凝聚映像。
为描述方便,列出以下条件:
(H1) 存在非负函数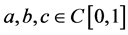 ,使得对任意
,使得对任意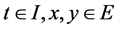 ,有
,有
 ,
,
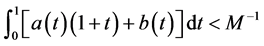 ;
;
(H2)对任意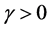 ,
,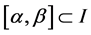 ,
,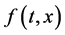 在
在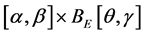 上是一致连续的,其中
上是一致连续的,其中
 ;
;
(H3) 存在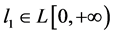 满足
满足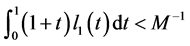 ,使得对任意
,使得对任意 ,E中的有界子集
,E中的有界子集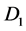 ,有
,有
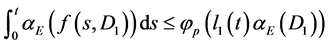
其中
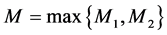 ,
,
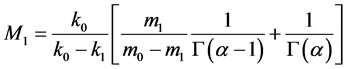 ,
,
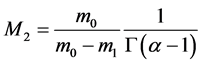 .
.
引理1 [8] (Schauder不动点定理) 令K是Banach空间E中的有界闭凸子集,T是K到其自身内的任一全连续映像,则T在K内至少有一个不动点。
引理2给定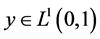 ,若
,若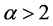 ,则边值问题:
,则边值问题:
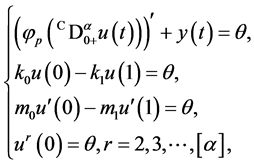 (3)
(3)
有唯一解
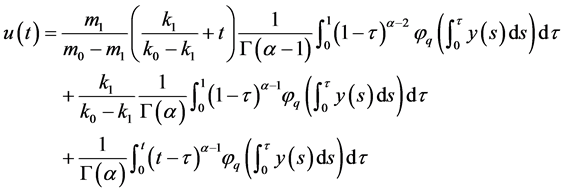 .(4)
.(4)
证明:由(3)知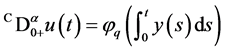 。
。
对上式两边积分及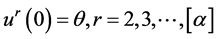 得
得
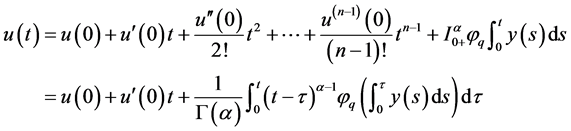 , (5)
, (5)
对上式求导得
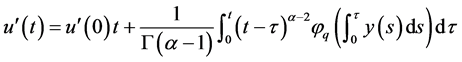
因此
 ,
,
 .
.
再由边值问题(3)的边界条件,可得
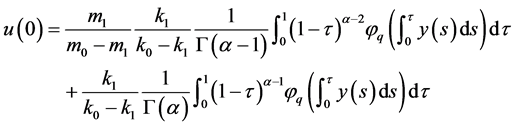 , (6)
, (6)
 . (7)
. (7)
将(6)、(7)代入(5),可得(4)成立。
引理3假设条件(H1)成立,则边值问题(1)等价于下面的积分方程:
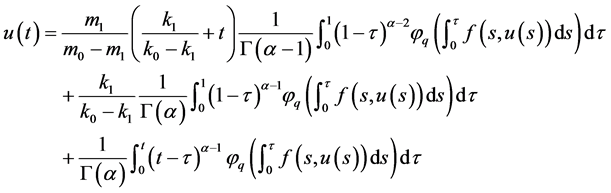
证明:引理3 的证明类似于引理2,在此略去。
对任意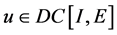 ,定义算子T:
,定义算子T:
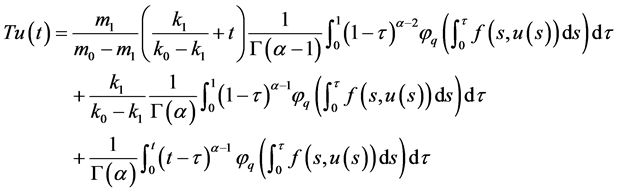 . (8)
. (8)
注1:引理3 说明边值问题(1)解的存在性等价于算子T的不动点的存在性。
引理4假设条件(H1)和(H2)成立,则算子 是连续有界的。
是连续有界的。
证明:首先,由(8)知
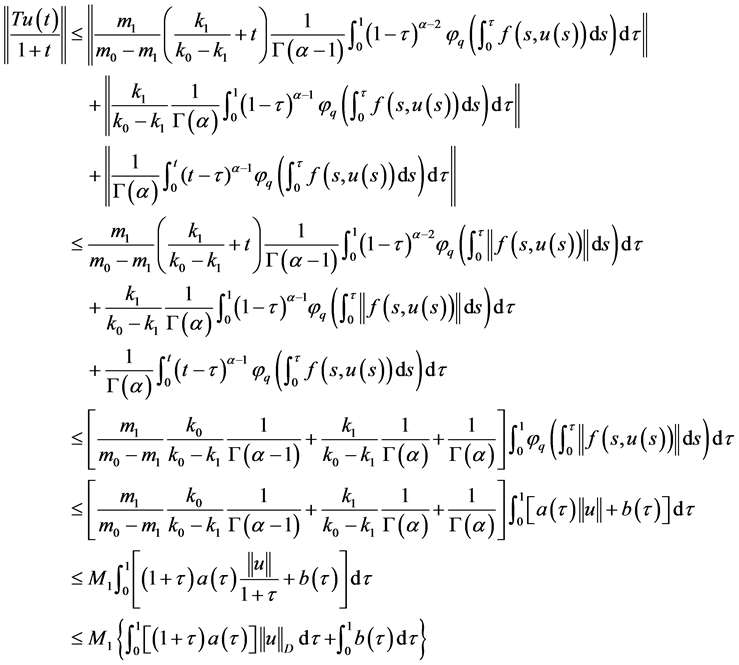 . (9)
. (9)
由(H1)知,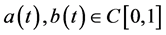 ,因此
,因此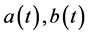 在I中是有界的,即存在正常数A和B,使得
在I中是有界的,即存在正常数A和B,使得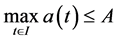 ,
,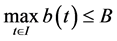 。
。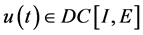 ,即:
,即: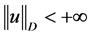 。再由(9)知
。再由(9)知
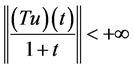 . (10)
. (10)
由(8)知
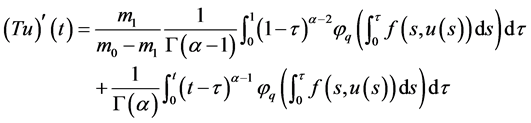 . (11)
. (11)
因此
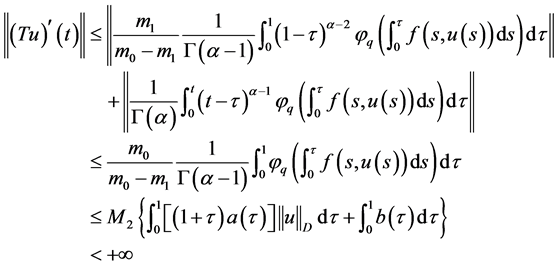 .(12)
.(12)
由(10)和(12)知,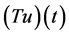 是良定义的并且
是良定义的并且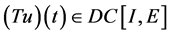 。
。
其次,算子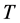 将
将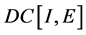 中的有界集映成有界集。下面仅需证明对任意
中的有界集映成有界集。下面仅需证明对任意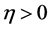 ,存在正常数
,存在正常数 ,使得对任意
,使得对任意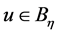 ,其中
,其中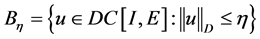 ,有
,有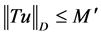 。令
。令
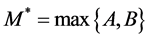 ,
,
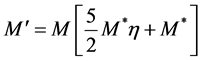 .
.
根据(H1)和(9)知
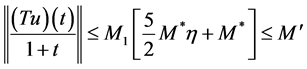 . (13)
. (13)
根据(H1)和(12)知
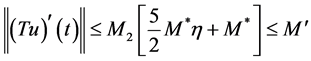 . (14)
. (14)
由(13)和(14)知,算子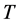 将
将 中的有界集映成有界集。
中的有界集映成有界集。
最后证明算子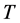 在
在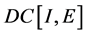 中连续。令
中连续。令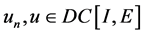 ,
, 。因此
。因此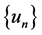 是
是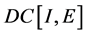 中的有界子集,即:存在常数
中的有界子集,即:存在常数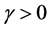 ,使得对任意
,使得对任意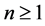 ,有
,有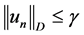 ,取极限得,
,取极限得,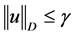 。另外,由(8)知
。另外,由(8)知
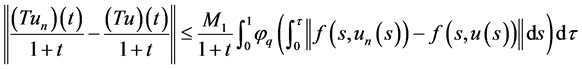 . (15)
. (15)
由(H2)知,对任意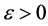 ,存在
,存在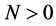 ,使得当
,使得当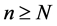 时,有
时,有
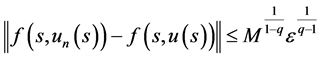 , (16)
, (16)
因此,对任意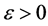 ,
,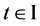 ,当
,当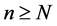 时,有
时,有
 . (17)
. (17)
同理,对任意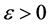 ,
,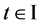 ,当
,当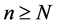 时,有
时,有
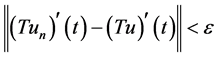 .
.
所以
 ,
,
即: 是连续的。引理得证。
是连续的。引理得证。
引理5假设条件(H1)成立并且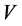 是
是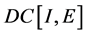 中的有界集,则
中的有界集,则 和
和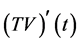 在
在 上是等度连续的。
上是等度连续的。
证明:为了证明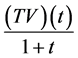 和
和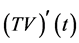 在
在 上是等度连续的,仅需证明下面的结论即可:
上是等度连续的,仅需证明下面的结论即可:
a) 对任意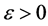 ,
,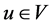 ,存在
,存在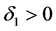 ,使得对任意
,使得对任意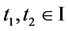 ,当
,当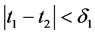 时,有
时,有
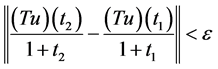 ;
;
b) 对任意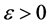 ,
, ,存在
,存在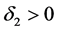 ,使得对任意
,使得对任意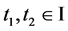 ,当
,当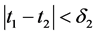 时,有
时,有
 .
.
首先证明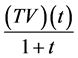 在
在 上是等度连续的。事实上,由条件(H1)知
上是等度连续的。事实上,由条件(H1)知
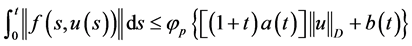 .
.
由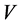 的有界性,存在
的有界性,存在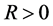 ,使得对任意
,使得对任意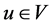 ,有
,有 。对任意
。对任意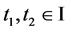 ,不妨假设
,不妨假设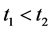 ,再由(8)及
,再由(8)及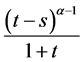 关于
关于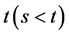 的单调性知
的单调性知
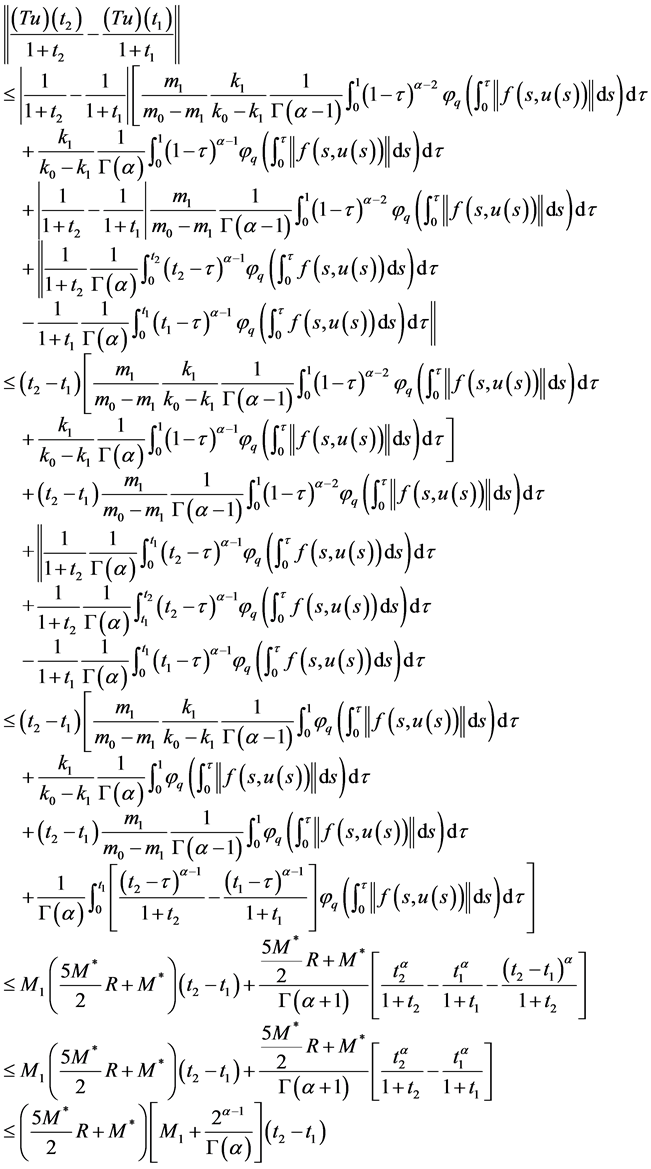 .
.
令
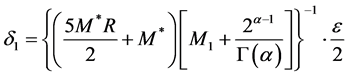 ,
,
因此对任意 ,
,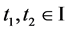 ,当
,当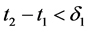 时,有
时,有
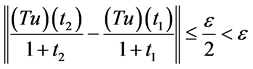 .
.
当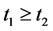 时,同理可证上式成立。所以
时,同理可证上式成立。所以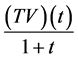 在
在 上是等度连续的。
上是等度连续的。
其次证明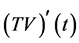 在
在 上是等度连续的。对任意
上是等度连续的。对任意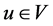 ,
,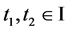 ,不妨假设
,不妨假设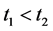 ,由(11)知,
,由(11)知,
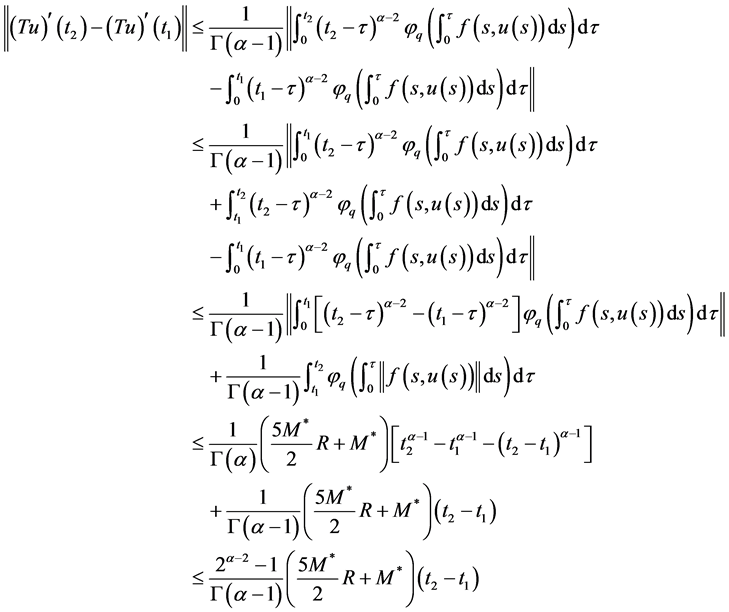
令

因此对任意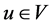 ,
, ,当
,当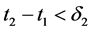 时,有
时,有
 .
.
当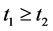 时,同理可证上式成立。所以
时,同理可证上式成立。所以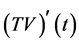 在
在 上是等度连续的。
上是等度连续的。
综上所述,引理得证。
引理6假设条件(H1)成立并且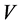 是
是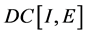 中的有界集,则
中的有界集,则
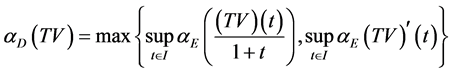 .
.
3. 主要结果
下面给出边值问题(1)解的存在性。
定理1 假设(H1)-(H3)成立,则边值问题(1)在 中至少有一个解。
中至少有一个解。
证明:我们仅需证明算子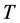 在
在 中至少有一个不动点即可。由(H1)知,我们可以选择实数
中至少有一个不动点即可。由(H1)知,我们可以选择实数 ,使得
,使得
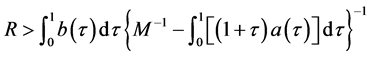 .
.
令
 .
.
首先证明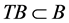 。事实上,对任意
。事实上,对任意 ,由(8)知
,由(8)知
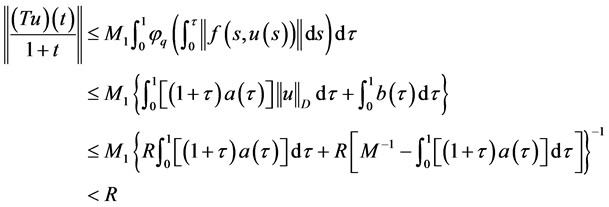 . (19)
. (19)
同理可证,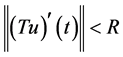 。由引理4知,
。由引理4知,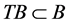 。令
。令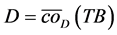 ,即:
,即: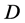 是
是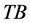 在
在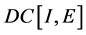 中的凸闭包。显然,
中的凸闭包。显然,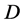 是
是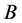 的非空有界凸闭包。由引理5知,
的非空有界凸闭包。由引理5知,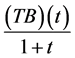 和
和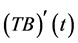 在
在 上是等度连续的,再由
上是等度连续的,再由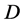 的定义知,
的定义知,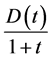 和
和 在
在 上是等度连续的。
上是等度连续的。
下证算子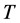 是由
是由 映到
映到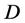 的严格集压缩映像。由
的严格集压缩映像。由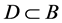 ,
,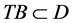 ,根据引理4知,
,根据引理4知, 是有界连续的。最后证明对任意
是有界连续的。最后证明对任意 ,有
,有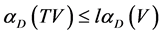 成立,其中
成立,其中
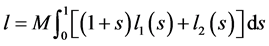 .
.
事实上,由引理6知,我们仅需证明
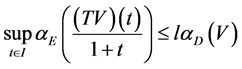 , (20)
, (20)
 . (21)
. (21)
先证(20)成立。由(H2)及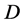 的定义知
的定义知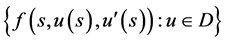 在
在 上是等度连续的。因此,由(H3)知,
上是等度连续的。因此,由(H3)知,
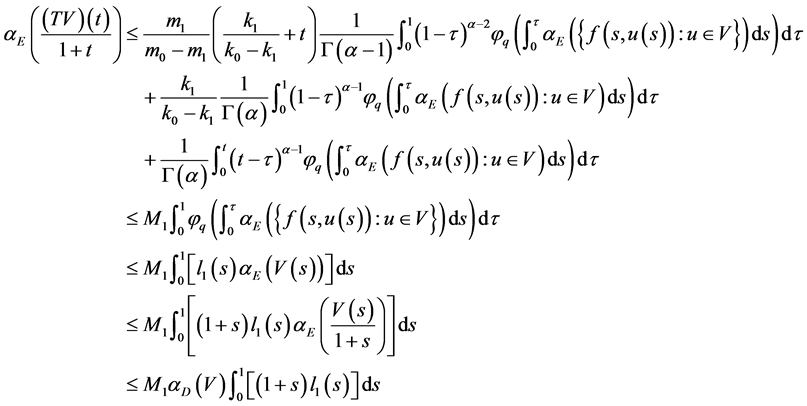 .
.
因为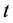 是任意的,所以(20)成立。同理可证(21)成立。由引理6及(19),(20)知,
是任意的,所以(20)成立。同理可证(21)成立。由引理6及(19),(20)知,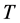 是由
是由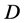 映到
映到 的严格集压缩映像。显然,
的严格集压缩映像。显然,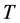 也是凝聚的。由引理1知,
也是凝聚的。由引理1知,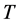 在
在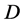 中只有一个不动点,即:边值问题(1)在
中只有一个不动点,即:边值问题(1)在 中至少有一个解。
中至少有一个解。
4. 结论
本文主要利用Kuratowski非紧性测度的性质和Sadovskii不动点定理,在Banach空间中得到了带有P-Laplacian算子的分数阶微分方程边值问题(1)解的存在性结果。
致谢
作者对审稿人提出的宝贵意见表示衷心的感谢。