1. 引言
具有牛顿势的平面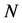 体问题是天体力学的重要组成部分,它研究的是具有正质量
体问题是天体力学的重要组成部分,它研究的是具有正质量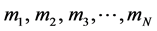 的
的 个天体,在仅受万有引力作用下的运动规律。本文仅考虑
个天体,在仅受万有引力作用下的运动规律。本文仅考虑 的情况。由牛顿三大定律和万有引力定律可知天体的运动满足:
的情况。由牛顿三大定律和万有引力定律可知天体的运动满足:
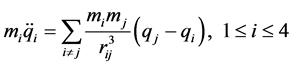 (1)
(1)
其中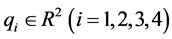 表示第
表示第 个天体的位置,
个天体的位置,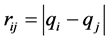 表示第
表示第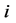 个天体与第
个天体与第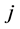 个天体之间的距离。
个天体之间的距离。
令 ,
, 为牛顿势函数
为牛顿势函数
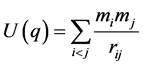 (2)
(2)
则方程组(1)可以写成
 (3)
(3)
由于在惯性坐标系下,质心做匀速直线运动或静止。故我们可以选取质心为坐标原点,即考虑空间
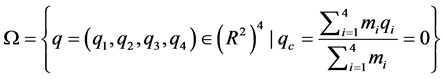 (4)
(4)
令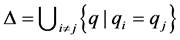 表示碰撞集,通常将
表示碰撞集,通常将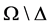 称为构型空间。
称为构型空间。
定义1.1 [2] 对于构型 ,如果存在一常数
,如果存在一常数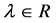 ,满足
,满足
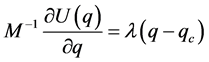
则称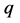 为中心构型(central configuration)。
为中心构型(central configuration)。
这一等式关于平面上的旋转、伸缩及平移仍然成立,如果一个中心构型能够由另一个中心构型通过旋转、伸缩及平移变换得到,则认为这两个中心构型是等价的。因此我们考虑中心构型时通常考虑这样的等价类。
对于平面四体共圆问题的中心构型(如图1所示),Cors和Roberts [1] 证明了:
定理1.2 [1] 如果质量满足假设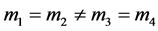 且
且 为共圆的中心构型,则构型
为共圆的中心构型,则构型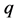 为等腰梯形。
为等腰梯形。
Cors和Roberts的证明仅从相对距离坐标入手,利用四个质点共圆的几何条件,通过复杂的计算和证明,建立四体共圆问题的中心构型方程,然后再经过一系列的讨论和化简后,利用质量的等量关系
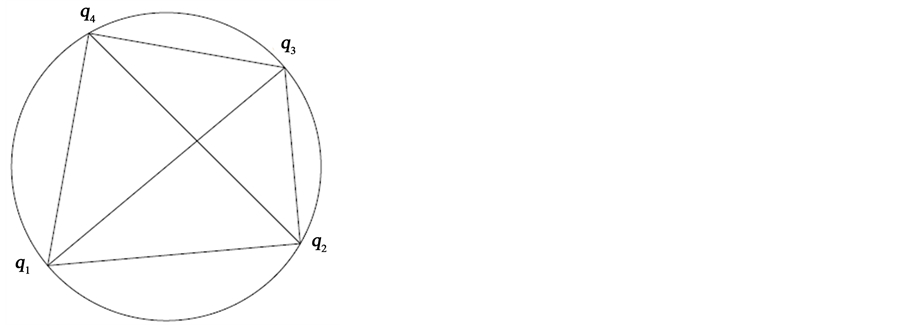
Figure 1. Planar four-body co-circular central configurations
图1. 平面四体共圆的中心构型
证明了该结论。本文采用有向面积的方法快速建立平面四体问题的中心构型方程,再直接利用质量的大小关系得到构型边长的大小关系,最后使用反证法给出了关于这一重要结果的一个简洁证明。
2. 一个重要的引理
令
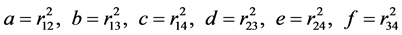 (5)
(5)
对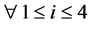 ,令
,令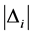 表示除去第
表示除去第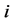 个顶点后剩余3个顶点所形成的三角形的面积。我们定义有向面积如下:
个顶点后剩余3个顶点所形成的三角形的面积。我们定义有向面积如下:
 (6)
(6)
显然有
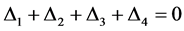 . (7)
. (7)
从文献 [3] 可知Cayley-Menger行列式为
 (8)
(8)
由于四体共面,所以相应四面体的体积为0,故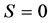 。
。
1900年,Dziobek [4] 证明了
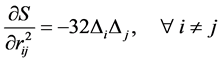 (9)
(9)
令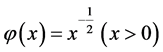 ,则整个系统的势函数与转动惯量可分别表示为
,则整个系统的势函数与转动惯量可分别表示为
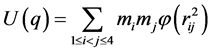 (10)
(10)
 (11)
(11)
其中 。
。
利用Lagrange乘子法,Dziobek [4] 给出了中心构型的一个等价刻画:中心构型是函数
 (12)
(12)
的驻点。其中 为Lagrange乘子,
为Lagrange乘子,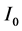 为初始转动惯量。从而对于
为初始转动惯量。从而对于 有
有
 (13)
(13)
即
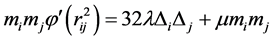 (14)
(14)
令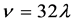 ,整理得
,整理得
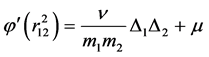 (15)
(15)
 (16)
(16)
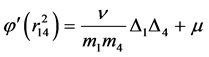 (17)
(17)
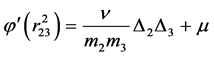 (18)
(18)
 (19)
(19)
 (20)
(20)
此外,在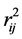 与
与 之间存在关系:
之间存在关系:
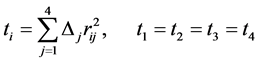 (21)
(21)
利用这个关系,Perez和Santoprete得到了下面的引理:
引理2.1 [5] 如果 形成中心构型,则等式(15)-(20)中的
形成中心构型,则等式(15)-(20)中的 满足关系:
满足关系: .
.
3. 定理1.2的证明
在证明定理1.2之前,我们先介绍下面的引理。
引理3.1 [6] 在定理1.2的假设条件下, 。
。
引理3.2 [6] 在定理1.2的假设条件下,若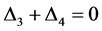 ,即
,即 ,则构型
,则构型 为等腰梯形中心构型。
为等腰梯形中心构型。
证明:当 时,易知
时,易知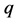 为梯形。再由等式(7)知
为梯形。再由等式(7)知
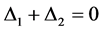 ,即
,即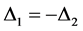 ,
,
从而
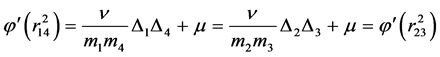
由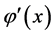 的单调性可知
的单调性可知 ,从而构型
,从而构型 为等腰梯形。
为等腰梯形。
下面我们来证明定理1.2。
证明:不失一般性,我们假设
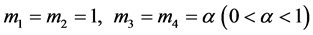
由引理3.2知我们只需证明:
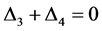 .
.
采用反证法,假设 ,则有以下两种情况:
,则有以下两种情况:
(i) ;
;
(ii)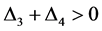 .
.
首先我们考虑情况(i):
由引理3.1可知
 (22)
(22)
由等式(7)知
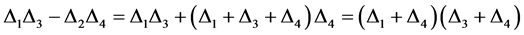
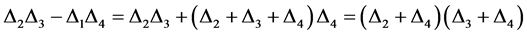
我们断言:
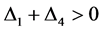
如果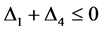 ,则
,则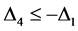
结合引理3.1有
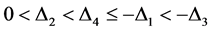 (23)
(23)
从而
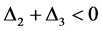
进一步有
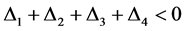
与等式(7)矛盾。所以
 (24)
(24)
即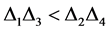 。
。
又由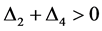 可得
可得
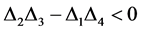 (25)
(25)
即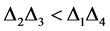 。
。
从而
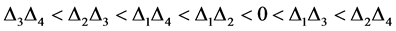 (26)
(26)
又因为 ,所以
,所以
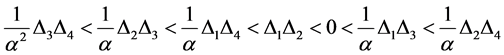 (27)
(27)
由引理2.1知
 (28)
(28)
又因为 关于
关于 单调递增
单调递增
所以
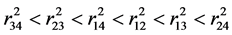 (29)
(29)
即
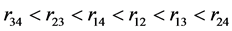 (30)
(30)
又因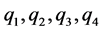 共圆,则
共圆,则 。
。
由余弦定理有
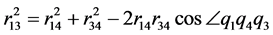
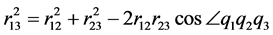
从而解得
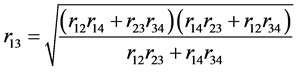 (31)
(31)
同理可得
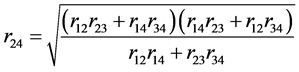 (32)
(32)
从而
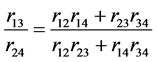 (33)
(33)
由关系式(30)有
 (34)
(34)
从而
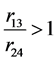 (35)
(35)
即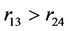 ,与关系式(30)矛盾。
,与关系式(30)矛盾。
从而情况(i)不成立。
类似可证明情况(ii)也不成立。
从而假设不成立,即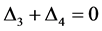 成立,完成了定理的证明。
成立,完成了定理的证明。
4. 结束语
本文利用有向面积,从质量的角度入手,并结合四体共圆的几何特征,给出了关于两对相邻等质量的四体共圆中心构型为等腰梯形这一结果的一个简洁证明。在之后的研究中,我们希望利用这个方法给出仅一对相邻质点质量相等的四体共圆中心构型为等腰梯形这一结论的不同的证明。进一步,我们希望能在具有两对相邻等质量的平面四体中心构型这一问题的研究中得到一些新的结果。
致谢
作者衷心感谢张世清教授在本文写作过程中的悉心指导与关心。
基金项目
中国自然科学基金(11671278)。
NOTES
*通讯作者。