1. 引言
Nim博弈是博弈论中最经典的模型,它有着十分简单的规则和无比优美的结论。它的规则如下:
有若干堆石子,每堆石子的数量都是有限的,两人交替拿走石子,合法的移动是“选择一堆石子并拿走若干颗(不能不拿)”,如果轮到某个人时所有的石子堆都已经被拿空了,则判负(因为他此刻没有任何合法的移动)。
1902年,Bouton [1] 给出了这个游戏的所有组合解。从此以后,通过修改Nim博弈的规则,各种各样的Nim类型的博弈就产生了,更多的可以参考 [2] [3] [4] [5] [6] [7] - [12] 。首先我们先来回忆一些组合游戏里的定义。
定义1 假设双方都采取最明智的策略,则对于一些状态,刚刚做完决策的游戏者有一定胜利的策略的状态(Previous Player wins the game)叫做P态。下一个做出决策的游戏者有一定获胜的策略的状态(Next Player wins the game)叫N态。
在有限的公平组合游戏中,P态和N态有如下的性质:
1) 所有终止状态都是P态;
2) 能一步到达P态的状态为N态;
3) 每一步都将到达N态的状态为P态。
要证明一个状态是N态,只需要证明它在一个合法的移动内可以变成一个N态,而要证明一个状态是P态,则需要证明它的任意一个下一步状态都是N态,所以寻找一个Nim类型组合游戏的P态就显得尤为重要。
定义2 两个非负整数的Nim和是指将这两个数换算成二进制以后的不进位相加所得到的值。更详细地,
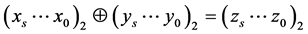 ,
,
其中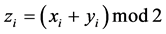 ,也即当
,也即当 为偶数时,
为偶数时,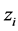 等于0,
等于0,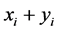 为奇数时,
为奇数时,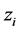 等于1。
等于1。
例3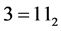 ,
, ,
, 。所以
。所以
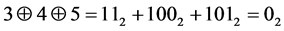 .
.
符号 在本文中,我们假设初始状态有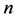 堆石子,每堆数目分别是
堆石子,每堆数目分别是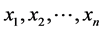 (数目可以重复,为了方便我们假设其为非降序排列)。我们用
(数目可以重复,为了方便我们假设其为非降序排列)。我们用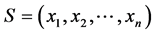 表示其初始状态。另外为了表述方便,我们用P1表示先手,P2表示后手。
表示其初始状态。另外为了表述方便,我们用P1表示先手,P2表示后手。
下面这个定理对普通的Nim博弈的所有的P态进行了一个刻画,那显然其所有对立面的状态就是N态。
Bouton定理 [1] 对于一个在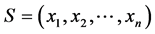 状态上进行的Nim博弈,它是P态当且仅当
状态上进行的Nim博弈,它是P态当且仅当
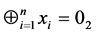 .
.
在这篇文章中,我们考虑一种新的游戏,K-L-Nim博弈,其规则如下。
有若干堆石子,每堆石子的数量都是有限的,两人交替移走石子,合法的移动是“选择一堆石子并拿走若干颗,不能不拿”,但是先手P1每次不能拿走k个石子(但可拿走多于或者少于k个石子),后手P2不能拿走l个石子(但可拿走多于或者少于l个石子),如果轮到某个人时所有的石子堆都已经被拿空了,则判负。
在第二部分,我们介绍当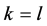 时该博弈的解;在第三部分,我们介绍当
时该博弈的解;在第三部分,我们介绍当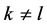 时的解。
时的解。
2. K等于L
在介绍我们的主要结论之前,我们先给出一些定义,以便我们能方便的证明我们的结论。
定义4 用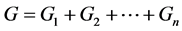 表示由单堆上进行的
表示由单堆上进行的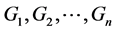 的Nim博弈组成的组合博弈。其中每个玩家可以在每一次走步中选择其中一个子游戏上进行。
的Nim博弈组成的组合博弈。其中每个玩家可以在每一次走步中选择其中一个子游戏上进行。
定义5 对于任意一个仅含一堆的Nim博弈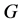 来讲,其Sprague-Grundy函数
来讲,其Sprague-Grundy函数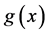 定义如下:对于其终止状态
定义如下:对于其终止状态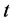 ,
,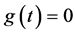 ,对于其他状态,
,对于其他状态,
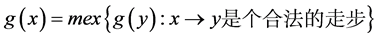 ,
,
其中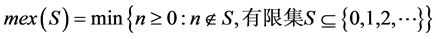 表示局外最小序数。
表示局外最小序数。
Sprague-Grundy定理 [10] 假设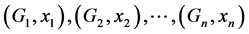 是
是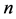 个单堆的Nim博弈及其初始状态。
个单堆的Nim博弈及其初始状态。 ,那么对于博弈
,那么对于博弈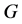 而言,其Sprague-Grundy函数
而言,其Sprague-Grundy函数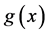 满足
满足
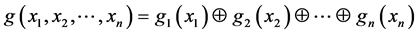 .
.
其中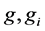 分别表示
分别表示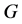 和
和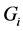 的Sprague-Grundy函数,其中
的Sprague-Grundy函数,其中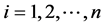 。
。
所以一旦知道一个博弈的Sprague-Grundy函数,我们就很容易的去分析与其相关的博弈。满足使得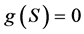 的状态
的状态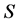 为P态,否则,为N态。
为P态,否则,为N态。
现在我们来考虑K-L-Nim博弈,其中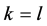 。
。
定理6 假设K-L-Nim博弈在石子数为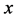 的单堆上进行,其中
的单堆上进行,其中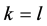 。那么我们有
。那么我们有
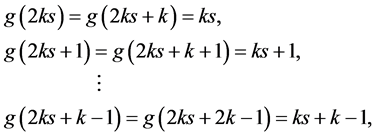
其中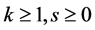 。
。
证明:我们主要对石子的总数采用数学归纳法。
假设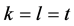 ,所以对两个玩家来说,他们的合法移动是每次拿走
,所以对两个玩家来说,他们的合法移动是每次拿走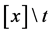 个石子。表1是
个石子。表1是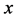 较小的时候的一些Sprague-Grundy函数值。
较小的时候的一些Sprague-Grundy函数值。
也即,

Table 1. The Sprague-Grundy function values of some small xs
表1. x较小的时候的一些Sprague-Grundy函数值
 ,其中
,其中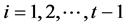 ;
;
 ,其中
,其中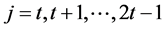 。
。
对于更一般的情形,我们有
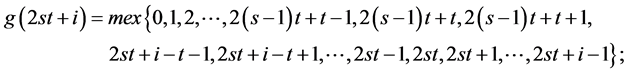
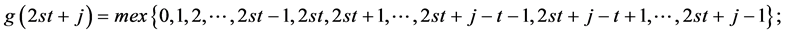
其中 ;
;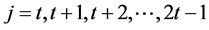 。
。
根据归纳假设,我们知道
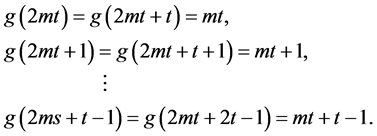
其中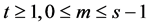 。
。
所以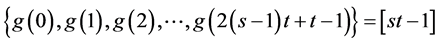 。
。
由于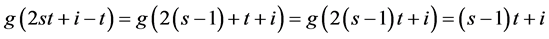 ,所以我们得到
,所以我们得到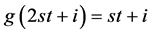 ,其中
,其中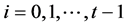 。同理,我们可以得到
。同理,我们可以得到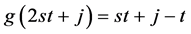 ,其中
,其中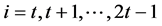 。由
。由 的选择的任意性我们完成了该定理的证明。□
的选择的任意性我们完成了该定理的证明。□
推论7:假设K-L-Nim博弈在石子数为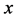 的单堆上进行,且
的单堆上进行,且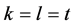 。那么Sprague-Grundy函数值如下
。那么Sprague-Grundy函数值如下
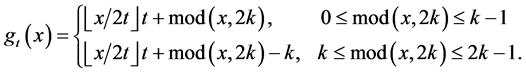
其中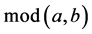 表示
表示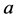 除以
除以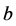 后的余数。
后的余数。
所以对于任意一个在状态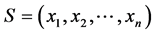 上进行的K-L-Nim博弈(
上进行的K-L-Nim博弈( ),我们可以将其看成是
),我们可以将其看成是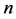 个单堆的Nim博弈的结合,并分别算出这
个单堆的Nim博弈的结合,并分别算出这 个初始状态的Sprague-Grundy函数值。如果这
个初始状态的Sprague-Grundy函数值。如果这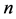 个值的nim和为0,则其初始状态为P态,否则为N态。
个值的nim和为0,则其初始状态为P态,否则为N态。
例8假设K-L-Nim博弈在初始态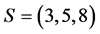 上进行,并且
上进行,并且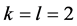 。所以
。所以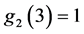 ,
,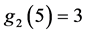 ,
,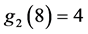 ,
, ,因此这是一个N态。
,因此这是一个N态。
3. K与L不相等
我们假设 。否则这个游戏就变成了普通的Nim博弈。
。否则这个游戏就变成了普通的Nim博弈。
定义9 如果一个状态在普通的Nim博弈中是N态,而它在K-L-Nim博弈的规则下不能在下一步转化成普通Nim博弈里的P态,那么我们说该状态是K-L-Nim博弈里的有缺陷的N态。
例10 假设K-L-Nim博弈在一个初始状态为 的状态上进行,其中
的状态上进行,其中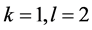 。显然
。显然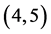 对于K-L-Nim博弈中的P1来说就是一个有缺陷的N态,因为
对于K-L-Nim博弈中的P1来说就是一个有缺陷的N态,因为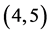 如果想变成普通Nim博弈里的一个P态,需要P1在第一步中从石子数为5的堆里拿走一颗石子,然而很显然,P1并不能做到。
如果想变成普通Nim博弈里的一个P态,需要P1在第一步中从石子数为5的堆里拿走一颗石子,然而很显然,P1并不能做到。
接下来,我们先看一下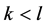 的情形。
的情形。
引理11 对于K-L-Nim博弈,其中 ,如果P2在一个有缺陷的N态上进行,那么他也有一个合法的移动,去留下一个有缺陷的N态给P1。
,如果P2在一个有缺陷的N态上进行,那么他也有一个合法的移动,去留下一个有缺陷的N态给P1。
证明:假设P2面对的状态为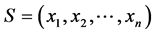 ,由于它是有缺陷的N态,故有
,由于它是有缺陷的N态,故有
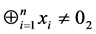 ,
,
并且存在一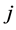 和
和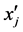 满足,
满足,
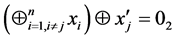 ,
,
其中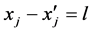 ,否则与缺陷的N态的定义相矛盾。这时P2可以从
,否则与缺陷的N态的定义相矛盾。这时P2可以从 中拿走
中拿走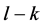 个石子,此时剩余状态为
个石子,此时剩余状态为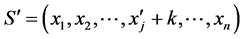 ,显然这对P1来说是一个有缺陷的N态。□
,显然这对P1来说是一个有缺陷的N态。□
定理12 对于K-L-Nim博弈,其中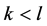 ,如果P1面对一个有缺陷的N态或者普通Nim博弈中是P态的状态,那么P2有必胜的策略。
,如果P1面对一个有缺陷的N态或者普通Nim博弈中是P态的状态,那么P2有必胜的策略。
证明:我们对石子的总数采用数学归纳法。无论P1面对一个有缺陷的N态还是普通Nim意义下的P态,在P1移动完以后,剩余的状态一定是普通状态里的N态,所以根据引理11以及Bouton定理,P2一定有策略使得他做完移动后剩余一个P态或者有缺陷的N态,由归纳假设可知,P2有必胜的策略。□
引理13 对于K-L-Nim博弈,其中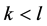 ,如果P2面对一个P态
,如果P2面对一个P态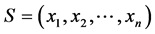 。只要
。只要 ,那么P2就有一个策略去留下一个带缺陷的N态给P1。
,那么P2就有一个策略去留下一个带缺陷的N态给P1。
证明:由于 是一个普通Nim博弈里的P态,所以有
是一个普通Nim博弈里的P态,所以有
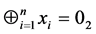 ,
,
不失一般性,我们假设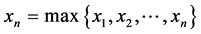 。P2的策略是从
。P2的策略是从 中拿走
中拿走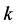 个石子。留下状态
个石子。留下状态 给P1,不难证明这个状态对于P1来讲是一个有缺陷的N态,因为P1若是想将状态
给P1,不难证明这个状态对于P1来讲是一个有缺陷的N态,因为P1若是想将状态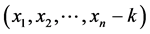 转化成普通Nim博弈里的P态,他必须在某一堆里拿走
转化成普通Nim博弈里的P态,他必须在某一堆里拿走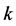 个石子,显然这是对于P1来讲是个不合法的移动。□
个石子,显然这是对于P1来讲是个不合法的移动。□
定理14 对于K-L-Nim博弈,其中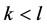 ,如果在P1走完第一步以后,剩余状态是在普通的Nim博弈里的一个P态,并且
,如果在P1走完第一步以后,剩余状态是在普通的Nim博弈里的一个P态,并且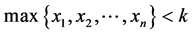 ,那么P1有必胜的策略,否则P2有必胜的策略。
,那么P1有必胜的策略,否则P2有必胜的策略。
证明:如果P1留下一个普通的Nim博弈里的一个P态给P2,并且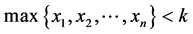 ,那么无论P2做出怎样的决策,既不能留下一个有缺陷的N态,也不能留下一个普通Nim博弈意义下的P态给P1,所以此时P1有必胜的策略。
,那么无论P2做出怎样的决策,既不能留下一个有缺陷的N态,也不能留下一个普通Nim博弈意义下的P态给P1,所以此时P1有必胜的策略。
定理的后半部分皆可由引理11,定理12以及引理13证明出来,在此不再赘述。□
参照上述几个引理及定理的P2的策略,不难得到下面这个推论。
推论15 对于K-L-Nim博弈,其中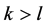 ,P1总有必胜的策略。
,P1总有必胜的策略。
至此,我们给出了该博弈在所有状态下的N态和P态。
致谢
感谢浙江师范大学“千人计划”朱绪鼎教授给本文的很多指导性的意见,也感谢审稿人给出了很多宝贵的修改意见。
基金项目
国家自然科学基金项目资助(KYZKJY11186)。