1. 引言
汽车仪表板杂物箱把手起到开启杂物箱的功能。客户对把手的滥用力要求较高，通常为(245 ± 4.9 N的载荷下持续10 ± 1.0秒钟时，把手不能断裂 [1] )。汽车仪表板杂物箱把手造型多变，强度影响因素多，结构复杂，一次性通过实验很困难，而且经过多轮整改才能满足标准要求，浪费了大量时间和费用。
田口方法是田口玄一博士在20世纪50年代至70年代，参考英国统计学家费希尔首创的实验设计方法和印度统计学家马哈拉诺皮斯提出的矩阵统计分析法，创立的稳健性质量方法体系 [2] 。目前已应用在汽车板料包边设计、汽车底盘设计、机械、电子、医疗等领域 [3] - [9] ，但是针对汽车仪表板杂物箱把手的研究几乎是空白。
本文以田口方法中的参数设计为分析思路，用仿真软件HYPERMESH 13.0和LS-DYNA为主要研究工具，确定理想功能、噪音因素和可控因素，建立内/外正交表和静态受力有限元模型。通过对信噪比(S/N，即对把手重载强度起到的有用作用/有害作用)和特性值(y，即把手能够承载的最大力值)的分析，找出了影响杂物箱把手重载荷强度的关键因素和最优化组合。
2. 设计方法
2.1. 设计程序
田口参数设计程序 [10] 见图1。
2.2. 设计目标
打开杂物箱盖的把手，在如图2所示的位置沿操作方向施加一大小为245 ± 4.9 N的载荷10 ± 1.0秒钟。增压件的形状应为15 × 40 mm的长方形。施力过程中，把手不能断裂。
2.3. 研究范围
杂物箱把手总成相关零部件见图3。
物理领域和功能领域见表1。
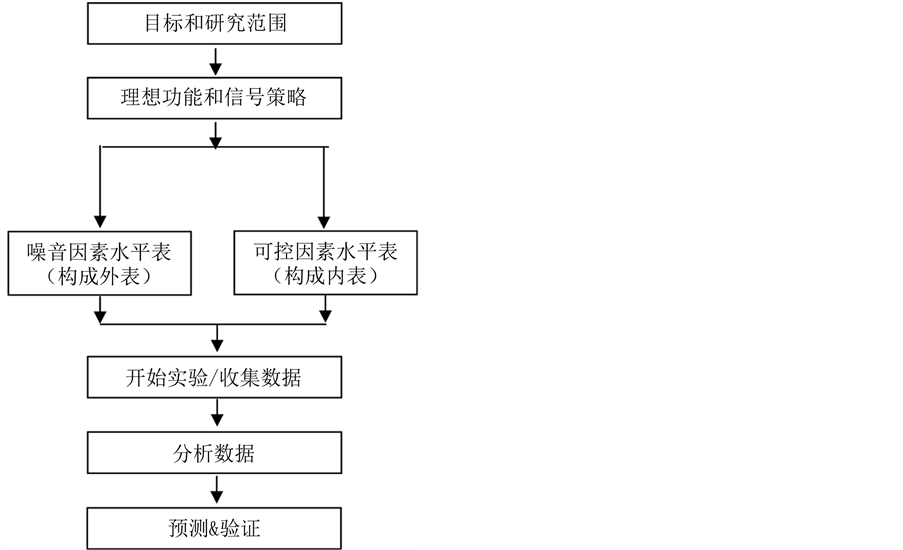
Figure 1. Procedure of Taguchi parameter design
图1. 田口参数设计程序
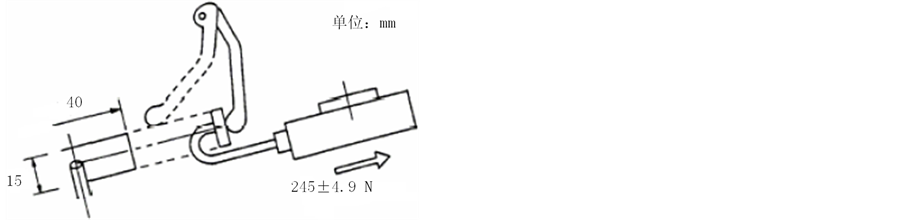
Figure 2. Procedure of Taguchi parameter design
图2. 田口参数设计程序
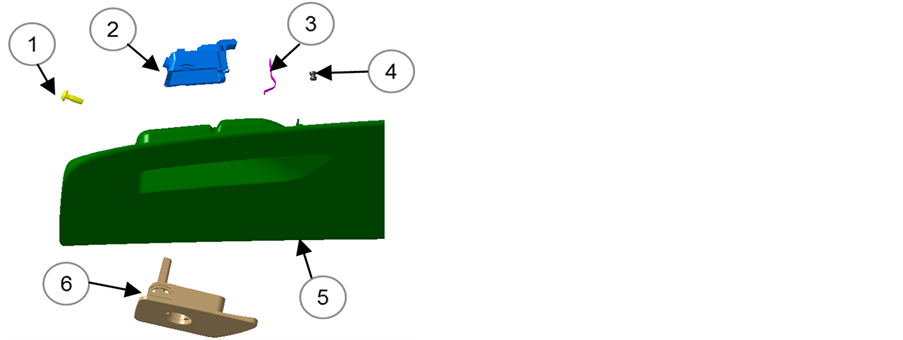
Figure 3. Parts of Glove box knob assembly
图3. 杂物箱把手总成相关零部件
通过识别物理领域和功能领域，结合以往设计经验，确定影响杂物箱把手重载荷强度的零部件是把手支座和把手。
2.4. 理想功能和信号策略
第一步，希望各零件之间的波动小，从正态分布图来看，数据集中，分散性小，即方差σ2越小越好；第二步，希望杂物箱把手能够承载的力无限大，即特性值y越大越好，见图4。
使用如下信噪比(S/N)公式来对杂物箱把手重载荷强度进行评价。
(1)
信噪比(S/N)是用来描述产品抵抗内/外干扰因素所引起的质量波动的能力，信噪比越大表示产品越稳健。公式中方差σ2越小，S/N越大；特性值y越大，S/N越大。
2.5. 噪音因素水平表
噪音因素是质量特性值波动的原因，是不能被设计者所控制的因素或者花大量费用才能控制的因素，分为外噪音、内噪音和产品间噪音：
1) 外噪音，由于环境因素和使用条件的波动或变化，引起特性值的波动。例如，温度、湿度、位置等。
2) 内噪音，由于在储存或使用过程中，随着时间的推移，发生材料变质、劣化现象而引起特性值的波动。例如，电器产品绝缘材料的老化等。
3) 产品间噪音，在相同生产条件下，生产制造出来的一批产品，由于人、机、料、法、环的变化，引起质量特性值的波动。
对于杂物箱把手重载荷，噪音因素见表2。N1为使质量特性值减小的组合，N2为使质量特性值增大的组合。
Table 1. Physical and functional domain of glove box knob
表1. 杂物箱把手的物理领域和功能领域
噪音因素示意见图5。
2.6. 可控因素水平表
杂物箱把手所要研究的可控因素水平见表3。
将可控因素表作为内表，噪音因素表作为外表，建立L18(2^1,3^7)田口正交表，见表4。
2.7. 开始实验/收集数据
对每一组数据创建有限元模型并进行分析，提取位移与力的关系曲线，在曲线中选取N1和N2情况下，曲线的顶点值，见图6。
实验数据见表5，单位为N。
2.8. 数据结果及分析
以第1组数据为例，进行计算。
特性值：
表2. 噪音因素表
表3. 可控因素表
(2)
方差：
(3)
信噪比：
(4)
同理求解其余17种组合的特性值(
)和信噪比(S/N)，见表6。
2.9. 预测及验证
根据表6的数据，分别计算可控因素A-H在不同水平下的特性值(
)和信噪比(
)，以A为例进行计算。
可控因素A在水平1时的特性值：
表4. 田口正交表
表5. 实验数据
Table 6. Characteristic value and S/N
表6. 特性值和信噪比
(5)
可控因素A在水平2时的特性值：
(6)
可控因素A在水平1时的信噪比：
(7)
可控因素A在水平2时的信噪比：
(8)
同理求解可控因素B-H在不同水平下的特性值(
)和信噪比(
)，见表7和表8。
分别将表7和表8的数据生成响应图，增加直观性，以便于判断。表7的响应图见图7，表8的响应图见图8。
从特性值(y)方面进行判断，结合表7的排序和图8各因素不同水平点的分散情况，可以看出因素D、G、H、B影响最大，最优化组合为A2，B1，C1，D1，E2，F3，G3，H1。
从信噪比(S/N)方面进行判断，结合表8的排序和图9各因素不同水平点的分散情况，可以看出因素C、B、D、A影响最大，最优化组合为A1，B2，C3，D1，E1，F3，G3，H2。
Table 7. Control factors characteristic value
表7. 可控因素的特性值
表8. 可控因素信噪比
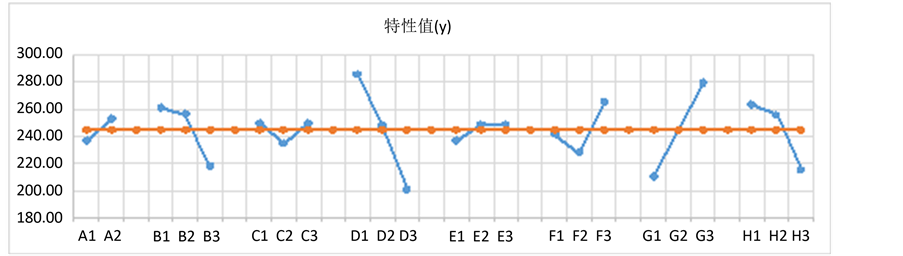
Figure 7. Response plot of control factors characteristic value
图7. 可控因素特性值响应图
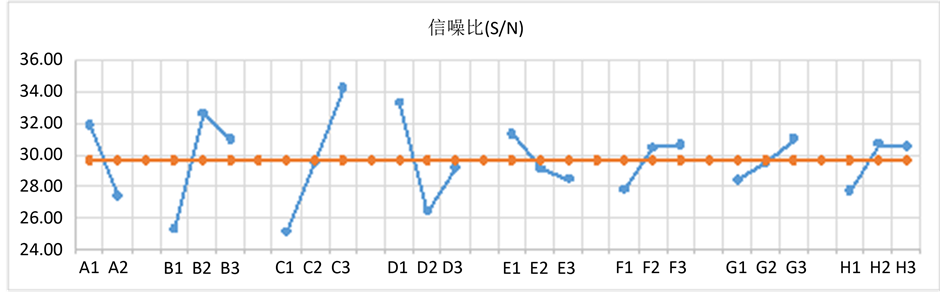
Figure 8. Response plot of control factors S/N value
图8. 可控因素信噪比响应图
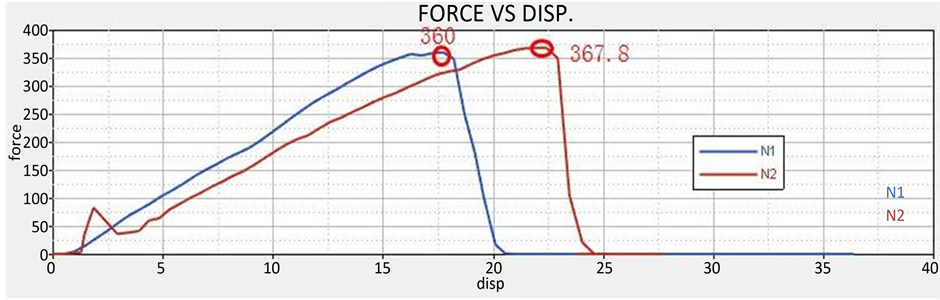
Figure 9. Optimal combination FEA model and result
图9. 优化组合的有限元模型和结果
综合考虑信噪比和特性值的最优组合以及结合杂物箱把手实际生产制造和装配经验，最终确定的优化组合为A1，B2，C3，D1，E2，F3，G3，H2。
预测优化组合的特性值(
)和信噪比(
)，计算公式如下：
根据表7中的数据和表6中特性值的平均值，预测优化组合的特性值(
)：
(9)
根据表8中的数据和表6中信噪比的平均值，预测优化组合的信噪比(
)：
(10)
根据优化的组合，重新设计杂物箱把手，并进行模拟分析，将模拟值与预测值作对比，以确认预测值的准确性。优化组合A1，B2，C3，D1，E1，F3，G3，H2有限元模型和结果见图9。
模拟结果
，
。
特性值：
(11)
方差：
(12)
信噪比：
(13)
对比模拟结果和预测结果可以看到，特性值y相差1 N，信噪比相差7.5 dB，两者非常接近，预测结果可信。
原设计与优化设计对比见表9，从表中可以看到，优化设计的杂物箱把手的重载荷强度达到364 N，大于245 N，较原设计强度提升了62%。信噪比提升了13.5 dB，将其带入公式14，计算得出杂物箱把手结构的稳健性提升了79%。
(14)
3. 结论
(1) 通过田口方法对影响杂物箱把手重载荷强度的因素水平进行仿真实验设计与求解，定量化地建立了不同因素水平与重载荷强度的关系。
(2) 找出汽车仪表板杂物箱把手优化设计的关键影响因素和优化组合A1 (把手打开时，把手与把手支座的后部间隙0 mm)，B2 (把手打开时，转轴部位间隙1.5 mm)，C3 (把手限位杆与把手支座的配合面宽度7 mm)，D1 (把手长度42 mm)，E2 (把手B面设计十字交叉筋)，F3 (转轴部位壁厚2.7 mm)，G3 (转
Table 9. Comparison original design and optimization design
表9. 原设计与优化设计对比
轴位置搭接量2.2 mm)，H2 (转轴圆角R0.3 mm)，为杂物箱把手的稳健性设计提供了工程解决方案。
(3) 通过对预测的验证，确认预测结果准确可信，因此可以使用本文的数据和插值方法，对不同造型的把手结构进行快速的强度计算，以快速判断新的设计能否满足重载荷强度要求。
基金项目
吉林省“双十工程”重大科技成果转化项目(20150301002GX)。