1. 引言
随着社会的发展,城市道路交通的压力越来越大,因此研究开放小区能否真正优化道路交通状况是社会广泛关注的一个问题。本文通过建立车辆通行的数学模型 [1] [2] ,对小区开放对周边道路通行的影响进行了研究,并定量分析了两种类型的小区开放后对周边道路通行的影响。
在第二节中,我们通过全有全无的分配方法结合Matlab程序解决了车辆在小区开放后的分流问题,接着利用所得出的流量计算车辆在行驶完某段路所需时间的公式得出计算结果,以此来建立模型。通过比较车辆行走相同路程的时间的多少来衡量小区周围道路的交通流畅程度,从而确定小区开放后的影响。
在第三节中,我们运用前面建立的模型,首先算出了开放前车辆绕小区一周的时间,然后以片块型和轴心型小区为例,进行定量的分析,分别得到了开放后,车辆绕行两种小区一周的时间,发现时间有不同程度的减少,所以我们得出了小区开放会对周围交通产生积极影响的结论。
最后我们对模型进行了总结。
2. 车辆通行的数学模型
本节中,我们建立了关于车辆通行的数学模型,可以获得小区附近的道路交通状况,模型中用到的分析指标包括交叉路口延误时间、行驶速度、车流量、行程时间等,最重要的是我们的模型可以作为研究开放型小区对周边道路的影响评价的依据。
本文中我们选取的车辆通行的分析指标主要有交叉口延误时间(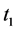 )、行驶速度(
)、行驶速度( )、车流量(
)、车流量( )、行程时间(
)、行程时间(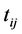 )等,介绍如下:
)等,介绍如下:
2.1. 交叉口延误时间
本文中采用交叉日平均延误计算方法 [3] 。平均延误计算的公式为:

其中: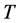 ——信号周期长度,s;
——信号周期长度,s;
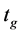 ——有效绿灯时间,s;
——有效绿灯时间,s;
 ——车道组V/C或饱和度,V/C指在理想条件下,最大服务交通量与基本通行能力之比。
——车道组V/C或饱和度,V/C指在理想条件下,最大服务交通量与基本通行能力之比。
2.2. 行驶速度
行驶速度以该小区附近道路交通安全条例所规定的速度为准,在后面的Matlab程序中我们使用的是60 Km/h进行进一步计算。
2.3. 车流量
对于车流量的研究,我们利用最短路径分配法,也称为全有全无分配方法。这是一个简单却十分有效的交通配流方法。以所有出行者都选取从出发地到目的地的最短路径为原则分配交通量。是其他各种交通分配方法的基础。OD交通量调查就是交通起终点的调查,OD交通量就是起点到终点之间的交通流量。英文ORIGIN和DESTINATION分别是“O”和“D”的来源,其中“O”表示出发点,“D”表示目的地。从一个起点到一个终点对(OD)间的最短路径,交通流如果只选择一条路线这样看起来是不合理的,所以OD往往不单单是一个点,而是一个矩阵,这样一来,OD的调查结果一般用一个表格表示,后又叫做OD矩阵。在附录1中我们对全有全无模型进行了Matlab程序的实现,程序中的 即为OD矩阵,通过程序我们可以定量计算出小区开放后,小区内部的支路所能分担的周围道路的车流量。
即为OD矩阵,通过程序我们可以定量计算出小区开放后,小区内部的支路所能分担的周围道路的车流量。
2.4. 行程时间
行驶时间的长短是车辆和行人判断道路状况时的最重要的标准之一,我们查找了大量文献后发现美国联邦公路局路阻函数(BRP函数)有不完善的地方。
原来的BRP阻抗函数为 [4] :

其中: ——从节点
——从节点 ~节点
~节点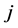 ;
;
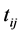 ——在路段
——在路段 上的实际花费的时间,s
上的实际花费的时间,s
 ——在路段
——在路段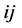 上的理想花费时间,s
上的理想花费时间,s
 ——在路段
——在路段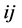 上的延误参数,
上的延误参数,
 ——路段
——路段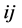 上的车流量,veh/h
上的车流量,veh/h
考虑到路上行人对车辆的影响以及非机动车辆对机动车辆的影响,我们在已有的研究基础的上得到了以上二者对车辆的影响系数,然后把影响系数加入到原有的BRP模型中,建立出符合我们需求的更加恰当的BRP模型。
我们得出的行人干扰修整系数 [4] 如下表1所示:
当非机动车交通量没有超过通行能力时系数取0.8,而当超过通行能力时干扰系数有以下公式计算得出 [3] 。

Table 1. Pedestrian interference trimming factor
表1. 行人干扰修整系数

其中: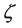 ——机动车受非机动车的干扰系数;
——机动车受非机动车的干扰系数;
 ——道路上实测得的非机动车的数量;
——道路上实测得的非机动车的数量;
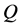 ——非机动车道路每米设计的通行能力;
——非机动车道路每米设计的通行能力;
 ——单向非机动车道宽度
——单向非机动车道宽度
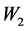 ——单向机动车道宽度
——单向机动车道宽度
根据以上分析,我们可以得到新的BRP阻抗函数模型 [4] :

在附录2中,我们通过Matlab程序实现了该模型的算法设计,该程序可以模拟出车辆行驶经过某段路程所花费的时间,结果中时间 越小,表明该道路交通越顺畅。
越小,表明该道路交通越顺畅。
3. 定量分析
3.1. 开放前小区对周围道路通行的影响
我们利用建立好的模型来分析两种结构不同小区开放后对周边道路的影响,这里,我们假设小区周边道路单向两条机动车道,一条非机动车道,共有四个信号灯,且两种类型的小区周长相等,下面我们给出一些参数的估计值(表2):
表2. 参数估计
根据以上数据,我们可以算出:
总的信号周期长度T:240 s (共四个信号灯,每个60 s)
总的有效绿灯时间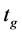 :100 s (共四个信号灯,每个25 s)
:100 s (共四个信号灯,每个25 s)
车辆在小区周边道路自由行驶所花费时间 :216 s
:216 s
根据我们已经建立的模型,利用Matlab程序编程,计算出车辆在小区周边道路行驶一周所需时间t为:4817.3849385239 s
3.2. 开放后各类型小区对周围道路通行的影响
下面我们模拟不同结构小区开放后,车辆在小区周边行驶一周所需时间:
3.2.1. 片块式布局
对小区开放后小区内部的三条支路会分担外围道路的车流量,由于在这种小区结构下(如图1),小区内部道路顺直平坦所以,通行能力比较好,我们给支路分配的权重也比较高,如图2。
这样根据我们已经编好计算支路分担车流量的程序,得到支路分担的总的车流量为:857.156 (包括机动车与非机动车)取整后为857辆/h。
按照机动车非机动车2:1的比例算出开放后小区支路分担周边自行车流量为285.667,取整为286辆/h,分担小区周边机动车流量为571辆/h,最后得到开放后小区周边的自行车流量为214辆/h,机动车流量为429辆/h。这样再根据程序计算出车辆在小区周围行驶一周所需时间t为:1924.66457309644 s可以看到通行花费的时间大幅度下降。
3.2.2. 轴线式布局
轴线式布局的小区(如图3)相比于片块式小区来说道路弯路较多但道路较宽,在中心广场处车辆容易产生堵塞,通行能力较上一种较差。但与片块式分布结构类似,所以我们给支路分配和上种结构相同的
权重,但在计算时要加上在中心广场处可能发生的延误,这里我们按照交叉路口的平均延误计算,得到在小区支路分担自行车流量286辆/h,机动车571辆/h的情况下,在中心广场发生的延误为:120 s,这样最后计算得到在轴线式小区开放后,车辆在小区周围行驶一周所需时间t为:2044.66457309644 s。可以看到虽然此类型小区开放后效果不如第一种效果好,但也分担部分了小区周围的通行压力。
4. 模型的总结
本文研究了小区开放对周边道路通行的影响,运用已建立的模型,定量地计算出了开放前后,车辆绕行小区一周的时间,得出了小区开放会对周围交通产生积极影响的结论。但在实际情况下,开放小区的好与不好是与小区本身的一些物理因素密切相关的,所以我们可以把模型推广到小区的建设与规划上,并加以改进,尽量使小区的建设能较好适应以后的变化,这样能有效地利用资源,有很强的现实意义。
致谢
本工作受到内蒙古自治区级大学生创新创业训练计划项目(201610126059)的资助,感谢创新基金导师的指导。
附录
附录1:此处主要参考[5]的程序思想
function [c,path,single,double]=floyd2(a,b)
%a--邻接矩阵
%b(i,j)--OD矩阵
%single--单向配流结果 double--双向配流结果
n=size (a,1);
c=a;
path=zeros (n,n);
fori=1:n;
for j=1:n;
path(i,j)=i;
end
end
for k=1:n;
fori=1:n;
for j=1:n;
if c(i,k)+c(k,j)
c(i,j)=c(i,k)+c(k,j);
path(i,j)=path(k,j);
end
end
end
end
single=zeros(n,n);
fori=1:n;
for j=1:n;
if abs(path(i,j)-j)<10^(-6);
j1=path(i,j);
single(j1,j)=single(j1,j)+b(i,j);
while abs(path(i,j1)-j1)<10^(-6);
i1=path(i,j1);
single(i1,j1)=single(i1,j1)+b(i,j);
j1=path(i,j1);
end
else
single(i,j)=single(i,j)+b(i,j);
end
end
end
fori=1:n;
for j=i:n;
double(i,j)=single(i,j)+single(j,i);
end
end
附录2:
%此程序是用来模拟车辆行驶某段路程所花费的时间,时间t越小,交通越顺畅q1=input('enter输入自行车流量''q1'':')%
q2=input('enter输入每米自行车的通行能力''q2'':')%
w1=input('enter输入非机动车道宽''o'':')%
w2=input('enter输入机动车道宽''p'':')%
v=input('enter输入机动车实际最大通行量''v'':')%
c=input('enter输入机动车最大通行能力''c'':')%
g=input('enter输入有效绿灯时间''g'':')%
T=input('enter输入信号灯周期''T'':')%
a1=input('enter输入车辆在某段路自由通行花费时间''a1'':')%
f=input('enter输入车流量''f'':')%
if(1>v/c)
min=v/c;
else
min=1;
end
d=0.5*T*(1-g/T)/(1-min*g/T);
n1=0.8-(q1/q2+0.5-w2)/w1;
if(n1<1&n1>0)
t=a1+0.15*(v/(c*0.8*(0.8-(q1/q2+0.5-w2)/w1)))^4*f+d
elseif(n1>1)
t=a1+0.15*[((0.8-q1/q2+0.5-w2)/w1*v)/(0.8*c)]^4*f+d
end