1. 引言
典型群的极大子群是群论研究的一个重要课题。作为一类特殊的极大子群,含根子群的极大子群也得到了广泛的研究。文献 [1] 中作者给出了域上线性群中含根子群的几类子群的极大性证明,并证明了域上线性群中含根子群的极大子群必属于这几类极大子群之一。辛群中含根子群的极大子群的研究可参见 [2] [3] [4] 。酉群中含根子群的极大子群的研究可参见 [5] [6] 。正交群中含根子群的极大子群的研究可参见 [7] 。本文主要研究交换环上线性群中含根子群的极大子群。
设 是含幺交换环,
是含幺交换环, ,
, 分别是
分别是 上的一般线性群和特殊线性群。设
上的一般线性群和特殊线性群。设 是单位阵,
是单位阵, 表示第
表示第 位置为1,其余位置为0的
位置为1,其余位置为0的 阶方阵,一般线性群
阶方阵,一般线性群 中的所有初等平延
中的所有初等平延
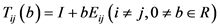
生成一个子群 ,它是
,它是 的一个子群。事实上,域
的一个子群。事实上,域 上有
上有 。容易验证
。容易验证

也是 的一个子群,我们把这样的子群以及它们在
的一个子群,我们把这样的子群以及它们在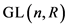 中的共轭子群称为根子群。
中的共轭子群称为根子群。
设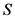 是
是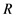 的极大理想,则
的极大理想,则 是域。对每个
是域。对每个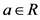 ,定义
,定义
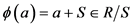
为 所在的模
所在的模 的同余类,则
的同余类,则

是环同态。设 ,对每个
,对每个 定义
定义
 . (*)
. (*)
则

是群同态。对任意正整数 ,
, ,记
,记
 .
.
则同态核
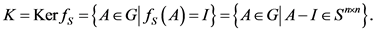
本文的主要结论如下:
定理1.1设 是含幺交换环,
是含幺交换环, ,如果以下子群
,如果以下子群 与
与 生成
生成 ,则
,则 及其在
及其在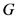 中的共轭都是
中的共轭都是 的含根子群的极大子群。特别地,
的含根子群的极大子群。特别地, 及其共轭是
及其共轭是 的含根子群的极大子群。
的含根子群的极大子群。
1) ,
,
 ,
,
2) ,
, ,
,
 ,
,
3) ,
,
 ,
, .
.
定理1.2设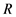 是含幺交换环,
是含幺交换环, 是
是 的子群,
的子群, 是
是 中含根子群的极大子群,则
中含根子群的极大子群,则 是以下两种类型之一:
是以下两种类型之一:
1) 存在 的某个极大理想
的某个极大理想 ,使
,使 是域
是域 上线性群
上线性群 的极大子群。当
的极大子群。当 时,
时, 一定是定理1的3类子群之一。
一定是定理1的3类子群之一。
2) 对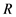 的每个极大理想都有
的每个极大理想都有
 ,
,
且 是
是 的极大子群。
的极大子群。
2. 定理的证明
在定理1.1的证明中,我们要先用群同态 来映到域
来映到域 上处理。所以我们先介绍域上的相关结论。从 [1] 定理1以及 [8] 定理3.6.1、3.7.2a容易得出以下引理。
上处理。所以我们先介绍域上的相关结论。从 [1] 定理1以及 [8] 定理3.6.1、3.7.2a容易得出以下引理。
引理2.1设 ,如果以下子群
,如果以下子群 与
与 生成
生成 ,则
,则 及其在
及其在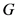 中的共轭都是
中的共轭都是 的含根子群的极大子群。特别的,
的含根子群的极大子群。特别的,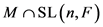 及其共轭是
及其共轭是 的含根子群的极大子群。
的含根子群的极大子群。
1)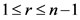 ,
,
 ,
,
2) ,
, ,
,
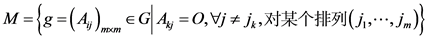 ,
,
3)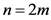 ,
,
 ,
,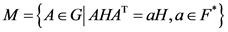 .
.
反过来, 时,
时, 中不包含
中不包含 的任一含根子群的极大子群必为上面所列子群之一。
的任一含根子群的极大子群必为上面所列子群之一。
注记文献 [1] 定理1以及 [8] 定理3.7.2a中第2类极大子群中有两个例外情形,很显然两个例外情形不满足“ 与
与 生成
生成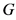 ”这一假设,不在我们讨论之列。
”这一假设,不在我们讨论之列。
下面,我们依次来给出本文两个定理的证明。
定理1.1的证明设 是
是 的极大理想,定义
的极大理想,定义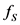 如(*)式,它的同态核
如(*)式,它的同态核 ,设
,设 的子群
的子群 真包含
真包含 ,则
,则 真包含
真包含 ,由引理2.1知,
,由引理2.1知, 是
是 的极大子群,因此有
的极大子群,因此有
 .
.
对每个 ,有
,有
 ,
,
因而存在 使得
使得
 .
.
这时有
 ,
,
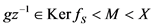 .
.
 包含
包含 及
及 ,从而包含它们的乘积
,从而包含它们的乘积 ,这说明了
,这说明了 中所有的
中所有的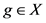 。从而
。从而 。这证明了
。这证明了 是
是 的极大子群。
的极大子群。
证毕。
定理1.2的证明设 是
是 的极大理想,定义
的极大理想,定义 如(*)式,首先,考虑到
如(*)式,首先,考虑到 的每个根子群
的每个根子群

在群同态 下的象为
下的象为
 ,
,
它是 的根子群。因此
的根子群。因此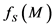 是
是 的含根子群的子群。如果存在
的含根子群的子群。如果存在 的真子群
的真子群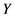 真包含
真包含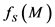 ,则
,则

是 的真子群且真包含
的真子群且真包含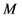 ,与
,与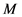 的极大性矛盾。
的极大性矛盾。
因此只有两种可能的情形:情形1. 是
是 的极大子群;情形2.
的极大子群;情形2. 。
。
情形1. 如果 不包含
不包含 ,此时
,此时 与
与 生成
生成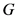 ,则
,则

是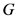 的真子群且包含
的真子群且包含 ,与
,与 的极大性矛盾。因此,此时
的极大性矛盾。因此,此时 。当
。当 时,由引理2.1知
时,由引理2.1知 是
是 的3类极大子群之一,于是
的3类极大子群之一,于是 是定理1.1所说的3类子群之一。
是定理1.1所说的3类子群之一。
情形2. 。
。
对每个 ,存在
,存在 使得
使得
 ,
,
从而
 ,
, .
.
如果 ,则由
,则由 包含
包含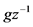 及
及 可知
可知 包含它们的乘积
包含它们的乘积 。这导致
。这导致 ,与
,与 是
是 的极大子群矛盾。因此
的极大子群矛盾。因此 不能包含
不能包含 ,
, 是
是 的真子群。如果存在
的真子群。如果存在 的真子群
的真子群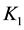 真包含
真包含 ,则
,则 是
是 的真子群且真包含
的真子群且真包含 ,与
,与 的极大性矛盾。这迫使
的极大性矛盾。这迫使 是
是 的极大子群。
的极大子群。
证毕。
注记我们猜想情形2中 的极大子群
的极大子群 具有以下形式:
具有以下形式:
 ,
,
其中, 是
是 中真包含于
中真包含于 的某个极大理想。此结论有待探究。
的某个极大理想。此结论有待探究。