采用光子晶体禁带法检测溶液浓度的新方法研究

New Method of Solution Concentration Detection Using Photonic Band Gap

摘要: 为了研究液体浓度检测用的光子晶体传感器特性，本文选择二维三角晶格光子晶体材料硅(Si)作为基底，在空气孔内填充不同质量摩尔浓度的待测溶液，计算出了溶液填充的光子晶体在不同偏振模式下的禁带宽度。给出了光子带隙中心所在频率位置的理论依据，应用光子晶体平面波展开法和已有的仿真数据。计算出了带隙中心所在频率位置与待测甲醇–水溶液浓度之间的关系。仿真结果表明，待测甲醇–水溶液的浓度与光子带隙中心频率之间存在正比例线性关系，本文选取溶液浓度检测范围为0.05~0.60 mol/L，并对不同结构产生的带隙位置进行了线性拟合，得到最终的拟合公式，这说明甲醇溶液浓度与带隙中心频率位置存在线性函数关系。

Abstract: In order to investigate the characteristics of the photonic crystal sensor for liquid concentration detection, in this paper, two-dimensional triangular lattice photonic crystal material silicon (Si) is chosen as the base, in which a solution with different mass mole concentrations is filled in the air hole to calculate the band gap of the photonic crystals with different polarization modes. The theoretical foundation of the frequency position center of photonic band gap is given. In addition, the relationship between the frequency position of the band gap center and the concentration of the methanol-water solution to be measured are calculated by using the planar wave expansion method and the existing simulation data. The simulation results imply that there is a positive proportional linear relationship between the concentration of the methanol-water solution and the center frequency of the photonic band gap. In this work, the range of solution concentration is 0.05~0.60 mol/L, and the linear fitting of the band gap position produced by different structures is obtained, and the final fitting formula is found, which indicates that the concentration of methanol solution is linear relationship with the center frequency of the band gap.

1. 引言

自从1989年Yablonovitch E和John S首次发现具有光子带隙结构的周期性介电材料后 [1] [2] ，光子晶体因其周期性结构产生的特殊效应而被广大研究者所关注。光子晶体被称为光学半导体，可以制作高性能光学器件，这使其在集成光电子学领域有重要的应用，在传感、太阳能电池、光纤通信等领域也有巨大的应用前景。近年来，高科技产业兴起，石化业与半导体业等使用含毒气体甚多，国内外均发生过气体外漏造成人员中毒、火灾等意外事件。对于具毒性气体储存、供应及反应废气排放，无论在安全侦测或防护装置等都需要精密检测，以确保工作人员的安全和持续环境清洁。液体或气体感测对于环境安全的侦测是必要的，适当的实时检测分析可保障工作安全、减少意外发生与提升居家生活质量。随着光子晶体功能化技术的不断完善和其独特的光学性能，以光子晶体为基本传感元件的传感器已经遍及多个领域，其中应用最为广泛的是生物医药领域 [3] 及化学物质浓度检测 [4] [5] ，尤其对于有毒易挥发危险性液体浓度的检测，体现出了独到的优势 [6] [7] ，已成为光电子技术，环境污染物检测和生物传感器技术的理论研究、结构设计等领域的研究热点 [8] 。质量摩尔浓度检测是保证产品质量和提高产品质量的重要技术手段 [9] 。有关测量质量摩尔浓度的方法有很多种，主要有：化学分析法，浮力法，重力法，静压法，分光法，同位素法，根据溶液导电性能检测浓度的方法等。但这些方法的工作原理及装置结构不同，使用场合也不同，并且各有不同的局限性和缺点，一般只能用于粗略地比对浓度差很大的待测溶液或者是所设计的检测系统元器件昂贵、系统稳定性差，不能广泛的应用于生产生活 [10] 。为了打破传统测量技术的局限性，本文以光子晶体的平面波展开法为基础，提出了基于光子晶体带隙宽度测量的质量摩尔浓度检测技术 [11] [12] 。给出了光子晶体带隙随待测溶液质量摩尔浓度的变化规律和质量摩尔浓度测量方面的模拟结果，为临床医学和生物化学中溶液浓度的检测提供了一个快速和简便的检测方法。

2. 基本理论

电磁波在二维光子晶体内传播，可分成在周期平面上传播及波矢量离面分量不为零的两种情形，在周期平面传播下其本证模分为：TM模式和TE模式，其方向如图1所示。一定条件下，两者将分别产生带隙，频率落在带隙内的某个特定方向上的偏振光在晶体里就不能传播，如果TE和TM模式的偏振光由相互重叠的部分，即产生完全带隙，那么落在完全带隙中的光沿任何方向都不能传播 [13] ，且TM 与TE模式的偏振光会与光子晶体的周期平面有关。本论文是以硅作为基底的二维三角形光子晶体为例，研究光子晶体在TM和TE模式下的禁带特性。

从Maxwell方程出发，考察介电常数 $\epsilon \left(r\right)$ 在z方向均匀分布，在x-y平面中周期排列的二维光子晶体中，光子晶体中的电场和磁场满足方程：

$\begin{array}{l}\frac{1}{{\epsilon }_r\left(r\right)}\nabla \times \left\{\nabla \times E\left(r,t\right)\right\}=-\frac{1}{c^2}\frac{{\partial }^2}{\partial t^2}E\left(r,t\right)\\ \nabla \times \left\{\frac{1}{{\epsilon }_r\left(r\right)}\nabla \times H\left(r,t\right)\right\}=-\frac{1}{c^2}\frac{{\partial }^2}{\partial t^2}H\left(r,t\right)\end{array}$ (1)

因为光子晶体周期性和时间没有关系，因此时间和空间可以分离。又由布洛赫理论可知，周期性介质中传播的波 $E\left(r\right)$ 和也应具有周期性。设其中含有n周期

$E\left(r\right)=E_{\kappa n}\left(r\right)={\displaystyle \underset{G}{\sum }{E}_{\kappa n}\left(G\right){\text{e}}^{i\left(\kappa +G\right)\cdot r}}$ (2)

$H\left(r\right)=H_{\kappa n}\left(r\right)={\displaystyle \underset{G}{\sum }{H}_{\kappa n}\left(G\right){\text{e}}^{i\left(\kappa +G\right)\cdot r}}$ (3)

上式中的 $c$ 为真空中光速， $\omega$ 为电磁波震荡频率， $\epsilon \left(r\right)$ 为相对介电常数， $H\left(r\right)$ 为磁场和电场强度矢量，是均为空间位移矢量 $r$ 的周期函数。在周期结构中，利用Bloch定理将展开磁矢量 $H\left(r\right)$ ，再基于 $H\left(r\right)$ 的平面波展开式，简化得以下特征方程 [14] [15] ：

$-{\displaystyle \underset{G^{\prime }}{\sum }K\left(G-G^{\prime }\right)\left(k+G^{\prime }\right)\times \left\{\left(k+G^{\prime }\right)\times H_{\kappa n}\left(G^{\prime }\right)\right\}}=\frac{{\omega }_{\kappa n}^2}{c^2}{H}_{\kappa n}\left(G\right)$ (TE) (4)

式(2)中， $K$ 为 ${\epsilon }_r^{-1}\left(r\right)$ 傅里叶级数 ${\epsilon }^{-1}\left(r\right)={\displaystyle \underset{G}{\sum }K\left(G\right){\text{e}}^{iG\cdot r}}$ 的展开系数，对三角晶格来说，Fourier系数 $K\left(G\right)$ 以下的解析表达：

$K\left(G\right)=\{\begin{array}{ll}\frac{1}{{\epsilon }_a}f+\frac{1}{{\epsilon }_b}\left(1-f\right),\hfill & G=0\hfill \\ 2f\left(\frac{1}{{\epsilon }_a}-\frac{1}{{\epsilon }_b}\right)\frac{J_1\left(\left|G\right|R\right)}{\left|G\right|R},\hfill & G\ne 0\hfill \end{array}$ (5)

式(4)中， $k$ 为是被限制于第一布里渊区的波矢量， $G$ 和 $G^{\prime }$ 为光子晶体的倒格矢。求的本征方程组后我们就可以用来计算矩阵表达式。式(5)中， $J_1$ 为一阶贝塞尔函数， $f=2\text{π}{R}^2/\sqrt{3}{a}^2$ 为空气圆孔占整个晶胞的百分比，即三角晶格的填充因子。为待测液体的介电常数， ${\epsilon }_b$ 为背景材料的介电常数。 $R$ 为介质柱截面半径。以本证方程求光子晶体的能带结构时，只有理论上应对所有的倒晶格点求和，才能精确地求出能带结构。但在实际上，由计算时间和计算机内存的限制，只能对有限个倒晶格点求和。

3. 分析与讨论

本文根据甲醇溶液检测的实际需求，采用数值仿真的方法进行研究，主要研究了以下内容：1) 三角形晶格分布方式进行建模，分析了光子晶体在相同外界条件下产生不同带隙的特性；2) 针对不同浓度的甲醇溶液填充于同结构的光子晶体时产生的最大带隙宽度百分比所在频率位置变化进行了数值仿真分析；3) 拟合出了带隙中心所在频率与甲醇溶液浓度的函数关系。

Figure 1. Section of triangular lattice 2D photonic crystal correspondence Brillouin zones

图1. 三角二维光子晶体截面及对应布里渊区

设相邻最近的空气孔之间的圆心间距为 $a=1\mu \text{m}$ ，空气孔的半径为 $R=0.35\mu \text{m}$ 。以材料Si( ${\epsilon }_a=11.7$ )为背景材料，以在相同情况下不同摩尔浓度的甲醇溶液填充于空气孔之中，甲醇溶液的介电常数为 ${\epsilon }_b$ 。

参考文献 [16] 得知在溶液温度为20℃ (293.15 K)时，不同浓度的甲醇–水溶液所对应的介电常数是不同的，如表1所示。

本文对三角形晶格结构的光子晶体进行禁带计算，得到表1所示的三角形几何排布的光子晶体在填充不同浓度甲醇–水溶液时所对应的带隙宽度比例分布数据。

甲醇–水溶液的质量摩尔浓度变化范围限定为5%到60% (单位：mol/L)。由图1到图2分别为背景材料硅与填充圆柱形空气孔的甲醇–水溶液构成的二维三角晶格光子晶体的带隙结构图。纵坐标采用标度化的无量纲频率ωa/2πc(a/λ)，而横坐标采用标度化的Bloch波矢 $k$ 。图1为在三角晶格分布的光子晶体中，圆孔中填充摩尔浓度为0.3 mol/L的甲醇–水溶液时所产生的横磁波(TM)和纵波(TE)光能带隙分布图。从图中可以看出，二维三角晶格晶体的TE模中只有3个能隙，而TM模中没出现带隙，其中禁带宽度比较大的带隙为Gap = 0.094 ~ 0.114，相应的带宽比例为Δ = 18.6%。考虑文章的篇幅，在不同质量摩尔浓度和介电常数情形下，对三角晶格光子禁带进行数值模拟计算得到了表1所示的最大禁带宽度和最大相对宽度百分比。

表1中的计算数据经过拟合生成溶液的质量摩尔分数与其仿真计算产生最大带隙宽度百分比的线性函数关系图。其中图2(a)表示甲醇–水溶液质量摩尔浓度与其介电常数之间的变化曲线图，在图中点各代表一定质量摩尔浓度所对应的介电常数值。从图2(a)可以看出，在一定温度下，溶液质量摩尔浓度与其介电常数呈现近似线性关系。图2(b)表示甲醇–水溶液浓度与最大带隙宽度百分比之间的线性拟合函数关系图，从图3可知，甲醇–水溶液浓度与最大带隙宽度百分比约呈线性关系。当溶液的质量摩尔浓度逐渐增大时，其对应的最大带隙宽度百分比变小，且呈一定的比例关系。通过上述的数值模拟可以得出：对于温度一定的溶液的质量摩尔浓度与最大带隙宽度百分比成近似线性关系，被测溶液质量摩尔浓度越大，产生的最大带隙宽度百分比越小，根据这个原理，通过光子晶体的光强大小变化来测定溶液的质量摩尔浓度。由图2(b)可知，由背景材料硅和填充溶液甲醇–水溶液构成的三角晶格光子晶体来说，随着介电常数的不同，出现的带隙宽度也不同，其最大带隙宽度百分比和质量摩尔浓度之间的线性拟合关系式为：

Table 1. The dielectric constant of the Methanol solutions of different molar concentration and lattice structure (293.15 K)

表1. 不同摩尔浓度的甲醇–水溶液的介电常数和带隙(293.15 K)

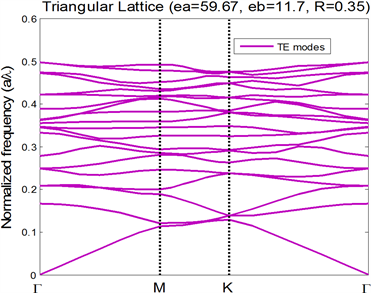(a) (b)

Figure 2. Dispersion diagram of the Triangular lattice (a)TE mode (b) TM mode

图2. 三角晶格结构模带隙图(a)TE模(b)TM模

(a) (b)

Figure 3. Linear fitting curve of methanol solution; (a) Relationship between Molfraction of methanol and dielectric constant; (b) Relationship between the maximum band gap width and the concentration of methanol solution

图3. 甲醇–水溶液浓度的线性拟合曲线；(a) 甲醇–水溶液质量摩尔分数和介电常数的关系；(b) 甲醇–水溶液浓度和最大禁带宽度之间的关系

$F_{\text{triangle}}=-0.0961C+0.2247$ (6)

式(6)中，F为最大带隙宽度百分比(%)，C为溶液的摩尔分数(mol/L)，线性拟合度分别为R² = 0.9855。通过以上研究内容可知，在实际应用光子晶体传感器的过程中，可以通过仿真计算出不同几何结构分布情况下产生的带隙中心频率，最后利用拟合方程求解出待测甲醇–水溶液的浓度。

4. 结论

本文应用平面波展开法，研究了以二维光子晶体为基础，以硅为基底材料的三角形晶格结构所产生的光子带隙特性，归纳出了光子带隙宽度百分比随溶液浓度变化的关系。模拟结果显示，在室温下利用甲醇–水溶液作为空气孔填充材料时，随着溶液的摩尔分数不断增加，光子晶体带隙宽度百分比在不断的减少。本文拟合函数拟合率最高可达R² = 0.9855，其线性关系可以应用于溶液浓度的检测。同时，本文的研究成果也将为化学物质浓度监测方面的研究提供参考意义。

基金项目

国家自然科学基金(11164030, 11664040, 11465019)的资助。