不同类型水电站群优化调度模型的大系统分解协调法研究

Research on Large-Scale System Decomposition and Coordination Method for Optimal Dispatching Model of Different Types of Hydropower Stations

摘要: 根据串并联水电站、混联水电站等不同类型水电站群的特点，建立了以发电量最大为目标的优化调度模型，模型同时考虑了水电站群间水力联系、电力联系等影响因素。针对不同类型水电站群优化调度模型构建了大系统分解协调算法，分别对模型问题分解、协调算法和收敛条件进行了详细的说明与推导。以清江流域水布垭、隔河岩、高坝洲水电站为例，建立了考虑梯级间流量传播影响和电力联系的3级串联水电站优化调度的大系统分解协调模型，大系统分解协调算法较传统算法计算效率更高，可以为大流域跨省区的复杂并联、混联水电站群多目标优化调度模型的构建、问题分解、以及算法等方面提供参考。

Abstract: According to the characteristics of different types of hydropower stations such as cascade and parallel hydropower stations, and mixed hydropower stations, the optimal dispatching model with the largest generating capacity was established. The model considers the influencing factors such as hydraulic connection and power connection between hydropower stations. A large system decomposition and coordination algorithm was used for the optimal scheduling model of different types of hydropower stations. The problem decomposition, coordination algorithm and convergence conditions were described and deduced respectively. A large-scale system decomposition and coordination model of three-stage cascade hydropower station considering the influence of the flow rate between the steps and the power connection was established, taking the Shuibuya, Geheyan and Gaobazhou hydropower stations in the Qingjiang River basin as an example. The proposed method is more efficient than the traditional algorithm, which can provide reference for the complex parallelization of the inter-provincial provinces in the large watershed, the construction of the multi-objective optimal dispatching model of the hybrid hydropower station group, the problem decomposition, and the algorithm.

1. 引言

水电站群是一个相互关联的复杂大系统，具有多级谱系结构，具有大系统分解协调的基础。吴昊等2015年研究了梯级水库群发电优化调度的大系统分解协调模型 [1] ，李爱玲研究了水电站水库群系统优化调度的大系统分解协调方法 [2] ，其主要对串联水库群优化调度进行了大系统分解协调研究。2013年李纯龙等对分解协调法进行了改进，建立了基于改进分解协调的大规模水电站群优化调度 [3] 。杨侃等针对梯级水电站群采用分解协调法进行了研究，建立了多目标分析的库群系统分解协调宏观决策方法 [4] 。高桂霞研究了大系统分解协调在库群防洪优化调度中的应用 [5] 。

目前，对于大系统分解协调及其改进算法在水电站群优化调度方面的研究，多数文献主要集中于研究串联或梯级水电站群的发电优化调度 [1] [2] [4] [6] [7] 、防洪优化调度 [5] 模型的算法，而用于研究解算复杂并联水电站群或混联水电站群等大流域跨省区的优化调度模型的相对较少。随着电子计算技术和基于生物学和人工智能的群智能优化算法的快速发展，水电站群优化调度模型解算方法的应用研究涌现了一批建立在基本解算方法之上的群智能优化算法，如遗传算法、粒子群算法 [8] 、蚁群算法 [9] 、蛙跳算法、狼群算法、混沌优化算法等算法及其改进算法。该群智能优化算法的研究主要应用于串联或梯级水电站群，对于复杂的并联、混联水电站群多目标优化调度的研究较少。

本文根据串并联水电站、混联水电站等不同类型水电站群的特点，构建考虑水电站群间水力联系、电力联系等影响因素，构建了以发电量最大为主目标的优化调度模型。针对不同类型水电站群优化调度模型构建了大系统分解协调算法，分别对并联水电站群、混联水电站群、串联水电站群优化调度模型的问题分解、协调算法、迭代终止条件和收敛条件等进行了详细的说明与推导。通过实例分析计算，大系统分解协调算法较传统算法计算效率更高，为大流域跨省区的复杂并联、混联水电站群多目标优化调度模型的构建、问题分解、以及算法等方面提供参考。

2. 不同类型水电站群大系统分解协调

2.1. 串联或梯级水电站群分解协调

对于串联或梯级水电站群调度问题，以调度期T内梯级总发电效益最大为目标，考虑河道流量传播影响因素，建立梯级短期优化调度数学模型。

串联或梯级水电站群优化调度模型的分解协调过程，笔者在三峡梯级短期优化调度的应用 [6] 进行了详细的推导与说明，本次实例分析推导了3级串联水电站群优化调度模型的大系统分解协调算法。

2.2. 并联水电站群分解协调

(1) 并联水电站群模型建立

对并联水电站群，上游水电站1也可以看作由梯级水电站群组成的一个子系统，如三峡–葛洲坝梯级；下游水电站2也可看作由梯级水电站群组成的子系统，如清江水布垭–隔河岩–高坝洲梯级。因此，并联水电站群可以由两并联梯级组成，分解协调方式与此类似，递阶控制结构为三级或多级递阶结构形式。

根据并联水电站群各电站之间是否存在相互关联的约束，分解协调问题具有与之对应的不同的形式，可分为以下几种：

A、电站间既无水力联系，也无电力联系

对于这种情况下的并联水电站群优化调度问题，就等价于各子系统(各电站)自身最优解的组合，即为整个系统的最优解。问题就转化为单一电站优化调度问题。

B、电站间无水力联系，但有电力联系存在

这种情况下各电站间通过电力的相互补偿使整个系统达到某种目标下的最优，如总发电量最大或总引水流量最小等，以电力联系(系统的全局约束)作为整个系统的耦合约束进行问题的分解与协调。该情况也是并联水电站群较为常见的联系形式。

C、电站间有水力联系，无电力联系

该情况下水力联系的形式之一为水头联系，即上游水电站1的出库流量通过影响下游河道水位 $Z{X}_{1,t}$ ，进而影响下游水电站2的尾水位流量关系曲线，即不同下游河道水位，水电站2对应不同的尾水位流量关系曲线。下游水电站2的尾水位 $Z{X}_{2,t}$ 可表示为自身出库流量 $Q_{2,t}$ 与河道水位 $Z{X}_{1,t}$ 的函数，公式如下：

$Z{X}_{2,t}=g_{2,zq}\left(Q_{2,t},Z{X}_{1,t}\right)$ (1)

该耦合约束式(1)是非线性的，系统是非线性耦合的系统。像这样的系统，进行分解协调要求函数 $g_{2,zq}(\cdot )$ 加性可分 [10] ，笔者对此问题还没有找到有效的分解协调方法。可采用其他方法如轮库迭代法等进行问题的求解。

D、电站间既有水力联系，也有电力联系

该情况是B、C两种形式的综合，也是并联库群系统最为复杂的情况，具体参见B、C，这里不在赘述。

下面以情况B为例，在满足并联电站群系统要求各时段出力情况下，以调度期T内各水电站总发电引水流量最小为目标，构造短期优化调度模型，进行问题的分解与协调，具体过程如下：

目标函数：

$\max QF={\displaystyle \underset{i=1}{\overset{2}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\sum }}Q{F}_{i,t}}}$ (2)

约束条件：

$V_{i,t}=V_{i,t-1}+\left(I_{i,t}-Q_{i,t}\right)\Delta t_{i,t}$ (3)

${\displaystyle \underset{i=1}{\overset{2}{\sum }}{N}_{i,t}}=N_t$ (耦合约束) (4)

$Z_{i,t,\min }\le Z_{i,t}\le Z_{i,t,\max }$ (5)

$N_{i,t,\min }\le N_{i,t}\le N_{i,t,\max }$ (6)

$Q_{i,t,\min }\le Q_{i,t}\le Q_{i,t,\max }$ (7)

式中：QF为水电站总的发电引水流量，m³/s； $Q{F}_{i,t}=Q_{i,t}-Q{q}_{i,t}$ ； $Q_{i,t}$ 、 $I_{i,t}$ 、 $Q{F}_{i,t}$ 、 $Q{q}_{i,t}$ 分别为第i水电站t时段出库流量、入库流量、发电引用流量、弃水流量，m³/s； $V_{i,t-1}$ 、 $V_{i,t}$ 为第i水电站t时段初、末库容，亿m³； $\Delta t_{i,t}$ 为第i水电站t时段计算时间长度，h或min； $Z_{i,t}$ 、 $Z_{i,t,\min }$ 、 $Z_{i,t,\max }$ 分别为第i水电站t时刻库水位、允许最小水位、允许最大水位，m； $N_{i,t}$ 、 $N_t$ 分别为t时段第i水电站出力、系统要求总出力，万kW； $N_{i,t,\min }$ 、 $N_{i,t,\max }$ 分别为第i水电站t时段的最小和最大出力，万kW； $Q_{i,t,\min }$ 、 $Q_{i,t,\max }$ 为第i水电站t时刻允许最小、最大引水流量，m³/s。

(2) 问题分解

根据对问题的描述，不必考虑子系统含有的一些不等式约束，构造该问题的Lagrange函数为：

$\begin{array}{c}L={\displaystyle \underset{i=1}{\overset{2}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\sum }}Q{F}_{i,t}}}+{\displaystyle \underset{i=1}{\overset{2}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\mu }_{i,t}\left[I_{i,t}-\left(V_{i,t}-V_{i,t-1}\right)/\Delta t_{i,t}-Q_{i,t}\right]}}\\ +{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\lambda }_t\left({\displaystyle \underset{i=1}{\overset{2}{\sum }}{N}_{i,t}-N_t}\right)}\end{array}$ (8)

为了使问题得到分解，选择与耦合约束相应的Lagrange乘子 ${\lambda }_t$ 作为协调变量，即采用目标协调法进行问题的分解协调。协调级给定的情况下，Lagrange函数的加性可分离形式为：

$\begin{array}{c}L={\displaystyle \underset{i=1}{\overset{2}{\sum }}{L}_i}={\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(Q{F}_{1,t}+{\lambda }_t{N}_{1,t}+{\mu }_{1,t}\left[I_{1,t}-\left(V_{1,t}-V_{1,t-1}\right)/\Delta t_{1,t}-Q_{1,t}\right]\right)}\\ +{\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(Q{F}_{2,t}+{\lambda }_t{N}_{2,t}+{\mu }_{2,t}\left[I_{2,t}-\left(V_{2,t}-V_{2,t-1}\right)/\Delta t_{2,t}-Q_{2,t}\right]\right)}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\lambda }_t\left(-N_t\right)}\\ ={\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(Q{F}_{1,t}+{\lambda }_t{N}_{1,t}\right)}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(Q{F}_{2,t}+{\lambda }_t{N}_{2,t}\right)}+Cont\end{array}$ (9)

由此，该问题可分解为如下两个子问题：

$\min L_1={\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(Q{F}_{1,t}+{\lambda }_t{N}_{1,t}\right)}$ (10)

$\min L_2={\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(Q{F}_{2,t}+{\lambda }_t{N}_{2,t}\right)}$ (11)

各子系统的约束条件，分别见式(3)、式(5)~(7)。

(3) 协调级算法

子问题除了满足Lagrange函数取得极值的最优性条件外，还需要引进一个迭代的协调级算法，根据对偶性原理，由于系统目标函数取极小，Lagrange函数的对偶函数关于 ${\lambda }_t$ 取极大，采用梯度法对 ${\lambda }_t$ 进行迭代，其协调算法的迭代公式为：

${\lambda }_t^{k+1}={\lambda }_t^k+{\alpha }_k{\left(\frac{\partial L}{\partial {\lambda }_t}\right)}^k={\lambda }_t^k+{\alpha }_k{\left({\displaystyle \underset{i=1}{\overset{2}{\sum }}{N}_{i,t}}-N_t\right)}^k$ (12)

式中：第k次迭代步长 ${\alpha }_k>0$ ，方向 $\frac{\partial L}{\partial {\lambda }_t}={\displaystyle \underset{i=1}{\overset{2}{\sum }}{N}_{i,t}}-N_t$ 为正梯度方向，因为Lagrange函数的对偶函数取极大。

协调级算法还要满足如下条件：

$\frac{\partial L}{\partial {\lambda }_t}={\displaystyle \underset{i=1}{\overset{2}{\sum }}{N}_{i,t}}-N_t=0$ (13)

通过协调级的逐步迭代，直到满足给定的终止条件，如两次迭代的 ${\lambda }_t$ 满足给定的精度要求，即 $\left|{\lambda }_t^{k+1}-{\lambda }_t^k\right|\le \epsilon$ 。

2.3. 混联水电站群分解协调

(1) 混联水电站群模型建立

对混联水电站群，以调度期T内各水电站总发电最大为目标，不考虑河道流量传播影响因素，构造短期优化调度数学模型，具体模型建立如下。对于考虑流量传播因素的情况，只需改动相应的水量连续方程即可。电站编号规则为先上游后下游，先支流再干流。

目标函数：

$\max E={\displaystyle \underset{i=1}{\overset{4}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{K}_i\cdot Q{F}_{i,t}\cdot h_{i,t}\cdot \Delta t_{i,t}}}$ (14)

约束条件：

$V_{i,t}=V_{i,t-1}+\left(I_{i,t}-Q_{i,t}\right)\Delta t_{i,t}$ (15)

$I_{2,t}=Q_{1,t}+Q{R}_{2,t}$ (关联约束) (16)

$I_{4,t}=Q_{2,t}+Q_{3,t}+Q{R}_{4,t}$ (关联约束) (17)

$Z_{i,t,\min }\le Z_{i,t}\le Z_{i,t,\max }$ (18)

$N_{i,t,\min }\le N_{i,t}\le N_{i,t,\max }$ (19)

$Q_{i,t,\min }\le Q_{i,t}\le Q_{i,t,\max }$ (20)

(2) 混联库群问题分解

分解方法同并联库群，把每一个水库作为一个子系统，共分解成4个子系统，选用关联约束，即耦合约束式(16)与(17)，进行构造Lagrange函数，同样不考虑子系统本身的不等式约束，因为其作用子系统内部，不影响问题的分解。

$\begin{array}{c}L={\displaystyle \underset{i=1}{\overset{4}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{K}_i\cdot Q{F}_{i,t}\cdot h_{i,t}\cdot \Delta t_{i,t}}}+{\displaystyle \underset{i=1}{\overset{4}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\mu }_{i,t}\left[I_{i,t}-Q_{i,t}-\left(V_{i,t}-V_{i,t-1}\right)/\Delta t_{i,t}\right]}}\\ +{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\lambda }_{1,t}\left(Q_{1,t}+Q{R}_{2,t}-I_{2,t}\right)}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\lambda }_{2,t}\left(Q_{2,t}+Q_{3,t}+Q{R}_{4,t}-I_{4,t}\right)}\end{array}$ (21)

式中： ${\mu }_{i,t}$ 、 ${\lambda }_{1,t}$ 、 ${\lambda }_{2,t}$ 分别为式(15)、式(16)、式(17)的Lagrange乘子。

选取与耦合约束相应的Lagrange乘子 ${\lambda }_{1,t}$ 、 ${\lambda }_{2,t}$ ，以及2、4两库的入库流量 $I_{2,t}$ 、 $I_{4,t}$ 作为协调变量，即目标协调与关联预估值协调入流相结合的混合模型法进行问题的分解。

在协调级给定的情况下，Lagrange函数的加性可分离形式如下：

$\begin{array}{c}L={\displaystyle \underset{i=1}{\overset{4}{\sum }}{L}_i}={\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(K_1\cdot Q{F}_{1,t}\cdot h_{1,t}\cdot \Delta t_{1,t}+{\lambda }_{1,t}{Q}_{1,t}+{\mu }_{1,t}\left[I_{1,t}-Q_{1,t}-\left(V_{1,t}-V_{1,t-1}\right)/\Delta t_{1,t}\right]\right)}\\ +{\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(K_2\cdot Q{F}_{2,t}\cdot h_{2,t}\cdot \Delta t_{2,t}+{\lambda }_{2,t}{Q}_{2,t}+{\lambda }_{1,t}\left(Q{R}_{2,t}-I_{2,t}\right)+{\mu }_{2,t}\left[I_{2,t}-Q_{2,t}-\left(V_{2,t}-V_{2,t-1}\right)/\Delta t_{2,t}\right]\right)}\\ +{\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(K_3\cdot Q{F}_{3,t}\cdot h_{3,t}\cdot \Delta t_{3,t}+{\lambda }_{2,t}{Q}_{3,t}+{\mu }_{3,t}\left[I_{3,t}-Q_{3,t}-\left(V_{3,t}-V_{3,t-1}\right)/\Delta t_{3,t}\right]\right)}\\ +{\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(K_4\cdot Q{F}_{4,t}\cdot h_{4,t}\cdot \Delta t_{4,t}+{\lambda }_{2,t}\left(Q{R}_{4,t}-I_{4,t}\right)+{\mu }_{4,t}\left[I_{4,t}-Q_{4,t}-\left(V_{4,t}-V_{4,t-1}\right)/\Delta t_{4,t}\right]\right)}\end{array}$ (22)

若不计常数项，则Lagrange函数可写为：

$\begin{array}{c}L={\displaystyle \underset{i=1}{\overset{4}{\sum }}{L}_i}={\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(K_1\cdot Q{F}_{1,t}\cdot h_{1,t}\cdot \Delta t_{1,t}+{\lambda }_{1,t}{Q}_{1,t}\right)}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(K_2\cdot Q{F}_{2,t}\cdot h_{2,t}\cdot \Delta t_{2,t}+{\lambda }_{2,t}{Q}_{2,t}\right)}\\ +{\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(K_3\cdot Q{F}_{3,t}\cdot h_{3,t}\cdot \Delta t_{3,t}+{\lambda }_{2,t}{Q}_{3,t}\right)}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}{K}_4\cdot Q{F}_{4,t}\cdot h_{4,t}\cdot \Delta t_{4,t}}\end{array}$ (23)

式(23)中每一项对应一个子系统的目标函数，分别对应水电站1~4，具体如下：

$\max L_1={\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(K_1\cdot Q{F}_{1,t}\cdot h_{1,t}\cdot \Delta t_{1,t}+{\lambda }_{1,t}{Q}_{1,t}\right)}$ (24)

$\max L_2={\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(K_2\cdot Q{F}_{2,t}\cdot h_{2,t}\cdot \Delta t_{2,t}+{\lambda }_{2,t}{Q}_{2,t}\right)}$ (25)

$\max L_3={\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(K_3\cdot Q{F}_{3,t}\cdot h_{3,t}\cdot \Delta t_{3,t}+{\lambda }_{2,t}{Q}_{3,t}\right)}$ (26)

$\max L_4={\displaystyle \underset{t=1}{\overset{T}{\sum }}{K}_4\cdot Q{F}_{4,t}\cdot h_{4,t}\cdot \Delta t_{4,t}}$ (27)

各子系统的约束条件，见式(15)、(18)~(20)。经过大系统的分解协调，把复杂大规模库群优化问题，转化为几个相对较小的子系统问题，每个子系统的求解是在第二级(上级)确定的协调变量已知的情况下进行的，协调变量值再根据第一级(下级)求得的子系统的解进行修正，逐次迭代直至获得一个最优解。

如前所述，在给定协调变量的情况下，各子系统间就不存在横向联系了，好像关联被切断，而其实是通过协调器保证各子系统间的关联。从而，就可以根据各子系统的自身特点，选择合适的寻优方法，通过协调使整个系统达到最优。

(3) 协调级算法

根据使总系统Lagrange函数取得极值，以满足关联平衡与关联预估的条件，则：

$\frac{\partial L}{\partial {\lambda }_{i,t}}=0$ (28)

$\frac{\partial L}{\partial I_{2,t}}={\mu }_{2,t}-{\lambda }_{1,t}=0$ (29)

$\frac{\partial L}{\partial I_{4,t}}={\mu }_{4,t}-{\lambda }_{2,t}=0$ (30)

由式(28)可得：

$I_{2,t}=Q_{1,t_i}+Q{R}_{2,t}$ (31)

$I_{4,t}=Q_{2,t_i}+Q_{3,t_i}+Q{R}_{4,t}$ (32)

由式(29)与式(30)可得：

${\mu }_{2,t}={\lambda }_{1,t}$ (33)

${\mu }_{4,t}={\lambda }_{2,t}$ (34)

根据Lagrange函数鞍点存在的条件，则：

$\frac{\partial L}{\partial Q_{2,t_i}}=K_2\cdot h_{2,t}\cdot \Delta t_{2,t}-{\mu }_{2,t}+{\lambda }_{2,t}=0$ (35)

$\frac{\partial L}{\partial Q_{4,t_i}}=K_4\cdot h_{4,t}\cdot \Delta t_{4,t}-{\mu }_{4,t}=0$ (36)

将式(33)与式(34)代入式(35)与式(36)，则有：

${\lambda }_{1,t}=K_2\cdot h_{2,t}\cdot \Delta t_{2,t}+K_4\cdot h_{4,t}\cdot \Delta t_{4,t}$ (37)

${\lambda }_{2,t}=K_4\cdot h_{4,t}\cdot \Delta t_{4,t}$ (38)

则由式(31)、式(32)、式(37)与式(38)构成协调级算法的迭代公式。

(4) 收敛条件

从理论上来说，迭代收敛条件如下：

$\left|I_{i,t}^{k+1}-I_{i,t}^k\right|\le {\delta }_i\left(i=2,4\right)$ (39)

$\left|{\lambda }_{i,t}^{k+1}-{\lambda }_{i,t}^k\right|\le {\epsilon }_i\left(i=1,2\right)$ (40)

$\left|E^{k+1}-E^k\right|/E^k\le e$ (41)

其中：k为迭代次数； ${\delta }_i$ 、 ${\epsilon }_i$ 、 $e$ 分别为相应精度要求。

迭代步骤与迭代终止条件同梯级库群问题的分解协调，子问题求解可根据实际情况采用POA等寻优方法。

3. 实例分析

本次以清江水电站群优化调度为例，分析说明3个水电站串联的水电站群优化调度模型的大系统分解协调算法。并联、混联的水电站群与梯级水电站优化调度模拟运算与串联类似，不再赘述。

清江梯级由水布垭、隔河岩、高坝洲等三座水电站组成，且电站各机组均已投产运行，梯级总装机容量为332.2万kW，梯级设计年发电量为79.22亿kW·h。清江流域是长江出三峡后的第一条大支流，发源于鄂西利川县齐岳山龙洞沟，于枝城市注入长江。干流全长423 km，总落差1430 m。流域呈南北窄、东西长的狭长形，流域面积约17,000 km²。

(1) 清江3级串联水电站群分解协调模型

以调度期内3级串联水电站群总发电量最大为目标，考虑河道流量传播影响因素，建立清江串联水电站群短期优化调度数学模型，具体如下：

目标函数：

$\max E={\displaystyle \underset{i=1}{\overset{3}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{K}_i\cdot Q{F}_{i,t}\cdot h_{i,t}\cdot \Delta t_{i,t}}}$ (42)

约束条件：

$V_{i,t}=V_{i,t-1}+\left(I_{i,t}-Q{F}_{i,t}-Q{q}_{i,t}\right)\Delta t_{i,t}$ (43)

$I_{i+1,t}=c_i+d_i{Q}_{i,t-{\tau }_i}+Q{R}_{i+1,t}$ (44)

$Z_{i,t,\min }\le Z_{i,t}\le Z_{i,t,\max }$ (45)

$N_{i,t,\min }\le N_{i,t}\le N_{i,t,\max }$ (46)

$Q_{i,t,\min }\le Q_{i,t}\le Q_{i,t,\max }$ (47)

根据大系统分解协调方法，可分解为下面三个子问题：

对水布垭水电站，优化调度模型为：

$\max L_1={\displaystyle \underset{t=1}{\overset{T}{\sum }}{K}_1\cdot Q{F}_{1,t}\cdot h_{1,t}\cdot \Delta t_{1,t}}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\lambda }_{1,t}\cdot d_1\cdot Q_{1,t-{\tau }_1}}$ (48)

对隔河岩水电站，优化调度模型为：

$\max L_2={\displaystyle \underset{t=1}{\overset{T}{\sum }}{K}_2\cdot Q{F}_{2,t}\cdot h_{2,t}\cdot \Delta t_{2,t}}+{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\lambda }_{2,t}\cdot d_2\cdot Q_{2,t-{\tau }_2}}$ (49)

对高坝洲水电站，优化调度模型为：

$\max L_3={\displaystyle \underset{t=1}{\overset{T}{\sum }}{K}_3\cdot Q{F}_{3,t}\cdot h_{3,t}\cdot \Delta t_{3,t}}$ (50)

上述三个子问题的约束条件均为式(43)~(47)。求解方法可采用逐步寻优算法(POA)。协调级算法：

$I_{2,t}^{k+1}=c_1+d_1{Q}_{1,t-{\tau }_1}^{k+1}+Q{R}_{2,t}$ (51)

$I_{3,t}^{k+1}=c_2+d_2{Q}_{2,t-{\tau }_2}^{k+1}+Q{R}_{3,t}$ (52)

${\lambda }_{1,t}^{k+1}=K_2\cdot h_{2,t}^k\cdot \Delta t_{2,t}+d_2\cdot K_3\cdot h_{3,t}^k\cdot \Delta t_{3,t}$ (53)

${\lambda }_{2,t}^{k+1}=K_3\cdot h_{3,t}^k\cdot \Delta t_{3,t}$ (54)

迭代终止条件：前后两次迭代目标函数值相对增长量小于某一精度要求。

(2) 模型解算结果与分析

调度期T为1 d，划分24个时段，即以1 h为一个调度单位。拟定两种不同典型的水布垭电站的日逐时入库流量过程，实际调度时采用短期或实时水文预报结果进行调度。给定水布垭日初水位400 m，日末水位400 m；隔河岩日初水位200 m，日末水位200 m；高坝洲日初水位80 m，日末水位80 m。水布垭最小下泄流量500 m³/s以满足航运要求，隔河岩下游通航流量200 m³/s，高坝洲下游通航流量120 m³/s。在VB6.0编译环境下，对清江梯级三座水电站的日发电优化调度分解协调法进行编程，求解了两种不同典型水布垭入流工况下的梯级日负荷曲线与各电站日负荷曲线。

梯级间流量传播系数采用相关分析法计算 [6] ，水布垭与隔河岩间流量传播系数c₁、d₁分别为17.16、1.259；隔河岩与高坝洲间c₂、d₂分别为0.997、1.081。

根据上述所建分解协调模型分别对两种工况进行求解。工况一：水布垭各时段入库流量500 m³/s；工况二：水布垭各时段入库流量1000 m³/s。工况一：水布垭、隔河岩、高坝洲日负荷过程和清江梯级日总负荷过程，见图1。工况二：水布垭、隔河岩、高坝洲日负荷过程和清江梯级日总负荷过程，见图2。

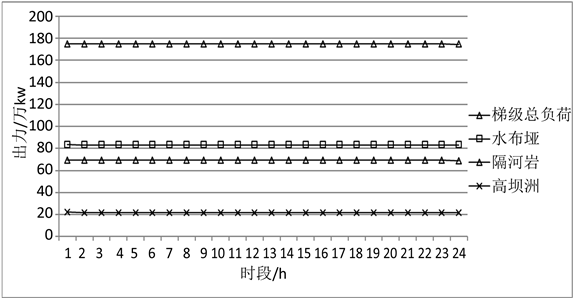
Figure 1. Daily load process of Case 1

图1. 工况一日负荷过程

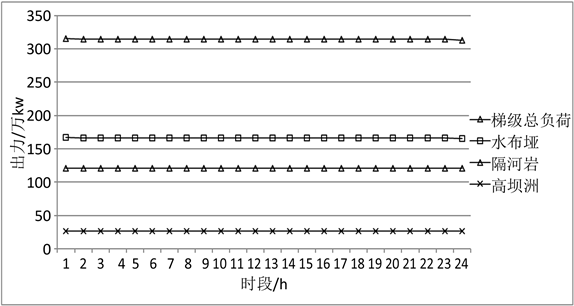
Figure 2. Daily load process of Case 2

图2. 工况二日负荷过程

在入流平稳的情况下，两种工况水库水位基本上均维持在高水位运行，整个梯级总发电量达到最大。从各梯级电站日负荷图1~图2，可以看出在开始一个时段出力较大，是因为水库起调水位为正常高水位，出流略微增加而致，当入流较大时(工况二)下游电站隔河岩与高坝洲均满出力运行。高水位运行也符合水库调度的一般规则。

大系统分解协调法较传统的动态规划算法，可以有效避免“维数灾”问题，大大提高模型解算效率，可以预见随着水电站群内并联或混联水电站数量的增加，分解协调法运算时间的优越性会更加明显。可以说明大系统分解协调法比传统的解算方法在解算水电站群优化调度方面有一定的优越性。

4. 结论

(1) 本文重点推导了串联、并联、混联水电站群优化调度模型的大系统分解协调算法的问题分解、协调级算法以及收敛条件等，为研究大系统分解协调算法在水电站群优化调度、多目标调度时提供一些参考。

(2) 大系统分解协调法在求解水电站群优化调度时比传统解算方法可有效避免维数灾，运算效率较高。

(3) 对于水电站群优化调度问题，其约束条件非常复杂，很难保证其目标函数与约束条件满足凸性要求，在实际求解问题时，可以从不同的初始点出发进行搜索最优解，即给定不同的初始调度线分别进行寻优，以其中最好的解作为问题的最优解。