1. 引言
在全球气候变化背景下,世界各国为应对水资源日趋短缺问题,建设和运营了多个跨流域调水工程,比如南水北调工程就是致力于解决我国北方地区水资源严重短缺的重大跨流域调水工程 [1] [2] 。由于跨流域调水工程是一个多流域、多水源、多工程、多主体、多目标的复杂水资源大系统,兼具有供水、蓄水、防洪、发电、航运等综合性功能,涉及多个省市和众多用水部门的利益,其工程运营与水资源配置具有极强的计划性和协同性,而供应链理念则体现了整体的协同性和利益最大化,因此,将供应链管理理念引入到跨流域调水工程运营管理中具有很强的可行性和适用性 [3] [4] 。
有不少学者把供应链管理理念引入到跨流域调水工程(主要是南水北调工程)运行管理中,对南水北调供应链管理、水资源定价、库存管理、长鞭效应、水资源配置以及供应链协调等若干问题进行了研究。① 关于南水北调东线供应链管理理论基础研究。王慧敏等(2004, 2005)早先论证了供应链管理理论与方法用于南水北调运营管理的可行性,并分析了南水北调东线供应链的概念模型和运作模式 [3] [4] 。陈志松等(2010)对社会责任与经济效益双重目标下南水北调工程运营管理的演化博弈及策略进行了研究 [5] 。② 关于南水北调东线供应链定价研究。王慧敏等(2008)研究了南水北调东线水资源供应链的联合定价模型 [6] 。张莉等(2008)建立了内外部市场价格歧视的南水北调东线水资源供应链定价模型 [7] 。Chen等(2013)研究了南水北调两部制定价机制及水资源优化配置方案 [8] 。③ 关于南水北调东线供应链库存研究。朱九龙等(2006, 2008)分别建立了南水北调水资源供应链VMI决策模型、非对称信息条件下的库存集中控制决策模型 [9] [10] 。侯艳红等(2008)构建了基于VMI契约的南水北调水资源供应链SRSS模型 [11] 。④ 关于南水北调东线供应链长鞭效应研究。朱九龙等(2005)分析了南水北调东线水资源供应链牛鞭效应的成因并提出了相应的控制对策 [12] 。⑤ 关于南水北调东线供应链配置研究。朱九龙(2007)建立了南水北调东线供应链水资源配置的多目标模型 [13] 。陈志松等(2010, 2011)分别建立了两次订购机会下的南水北调Newsvendor优化配置模型 [14] [15] 。⑥ 关于南水北调东线供应链协调与合作研究。侯艳红等(2009)建立了南水北调东线供应链灵活订货量契约的动态规划模型 [16] 。Chen等(2012)研究了战略顾客行为下南水北调供应链优化与协调 [17] 。Chen等(2012)建立了南水北调供应链合作运营的非对称Nash讨价还价模型 [18] 。Wang和Chen等(2012)研究了南水北调供应链优化定价与协调方案 [19] 。显然,现有文献较少有从合作博弈视角进行跨流域调水供应链合作利益分配的相关研究。
学者们对水资源合作配置也进行了不少研究,比如Young等(1982)将核与核仁解运用于水资源开发中的成本分摊 [20] ;Tisdell等(1992)运用了不同的合作博弈方法分析水权合作配置,从而试图找出最公平的分配方案 [21] ;Lejano等(1995)运用规范化的核仁解分析了南加州的水循环利用工程运营,并于传统的核仁解与Shapley值方法进行了对比分析 [22] ;Teasley等(2007)运用合作博弈的方法分析了跨界湖泊的水资源合作配置 [23] ;Wang等(2003, 2007, 2008)运用核仁解和Shapley值方法分析了流域水资源合作配置 [24] [25] [26] 。但现有的研究缺乏对跨流域调水供应链合作运营机制的探讨,尚未从合作博弈视角对跨流域调水供应链优化定价和配置及合作利益分配进行过深入研究。
跨流域调水供应链运作过程中,往往缺乏有效的参与主体合作运营机制,上、下游参与主体倾向于追求自身利益最大化,从而导致参与主体与工程整体的运营目标相偏离。如何兼顾个体理性与集体理性、构建有效的供应链合作机制、提高工程运营绩效、实现参与主体利益的帕累托改进,成为跨流域调水供应链运营管理中亟需解决的科学问题。本文尝试分别从非合作博弈视角和合作博弈视角,构建不同联盟组合下跨流域调水供应链的非合作博弈模型以及基于三种核仁方法和Shapley值方法的合作博弈模型,并进行对比数值分析。
2. 模型假设
跨流域调水工程是一个多水源、多目标和多工程,抽、蓄、供水并举的大型跨流域复杂大系统,从供应链视角,可以概化为由系统供应商、本地分销商和外地分销商构成的水资源供应链系统。为建模需要,用1标记本地分销商,2标记外地分销商。本文假设系统供应商、本地和外地分销商单位平均调水成本分别为c、
和
,系统供应商本地和外地水资源批发价分别为
和
,本地和外地分销商终端水价分别为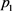 和
,本地和外地水市场规模分别为
和
,本地和外地多年平均降水量分别为
和
,本地和外地分销商水资源订购量分别为
和
,本地和外地水资源需求关于价格变动的敏感程度分别为
和
,本地和外地用户对降水量的利用比率分别为
和
,且
,供应商和外地分销商对降水量的利用比率分别为
和
,且
,且
。终端水资源需求受降水和水价的影响,降水量越大,用户可用的免费水资源越多,则水资源需求越小;水价越高,则水资源需求越小。因此,本地和外地终端水资源需求函数分别为
,
。则有
,
。本文的决策变量为:本地和外地分销商终端水价
和
,供应商本地和外地水资源批发价
和
。
和
,本地和外地水市场规模分别为
和
,本地和外地多年平均降水量分别为
和
,本地和外地分销商水资源订购量分别为
和
,本地和外地水资源需求关于价格变动的敏感程度分别为
和
,本地和外地用户对降水量的利用比率分别为
和
,且
,供应商和外地分销商对降水量的利用比率分别为
和
,且
,且
。终端水资源需求受降水和水价的影响,降水量越大,用户可用的免费水资源越多,则水资源需求越小;水价越高,则水资源需求越小。因此,本地和外地终端水资源需求函数分别为
,
。则有
,
。本文的决策变量为:本地和外地分销商终端水价
和
,供应商本地和外地水资源批发价
和
。
跨流域调水工程中,系统供应商、本地和外地分销商在不同联盟{WS},{LD},{ED},{LD, ED},{WS, LD},{WS, ED},{WS, LD, ED}的目标函数分别为:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
从非合作博弈视角和合作博弈视角,本文拟分别构建不同联盟组合下跨流域调水供应链的非合作博弈模型以及基于核仁方法和Shapley值方法的跨流域调水供应链合作博弈模型,并进行对比数值分析。
3. 不同联盟组合下跨流域调水供应链非合作博弈与优化模型
3.1. 跨流域调水供应链非合作博弈模型
跨流域调水供应链非合作博弈决策次序为:系统供应商首先决策本地和外地水资源批发价
和
,进而,本地和外地分销商分别同时决策终端水价
和
,则有跨流域调水供应链的非合作博弈模型如下:
(8)
求解该非合作博弈问题,可得本地和外地水资源均衡批发价、终端水价和订购量分别为:
(9)
(10)
(11)
(12)
(13)
(14)
系统供应商、本地分销商和外地分销商的均衡利润分别为:
(15)
(16)
(17)
3.2. 跨流域调水供应链局部联盟的非合作博弈模型
跨流域调水供应链局部联盟共分为三种情形:局部联盟组合{WS},{LD, ED},局部联盟组合{WS, LD},{ED},局部联盟组合{WS, ED},{LD},下面将分别构建这三种局部联盟情形下的非合作博弈模型。
(1) 局部联盟组合{WS},{LD, ED}的非合作博弈模型
跨流域调水供应链局部联盟组合{WS},{LD, ED}非合作博弈决策次序为:系统供应商首先决策本地和外地水资源批发价
和
,进而,本地和外地分销商组成的联盟决策终端水价
和
,则有局部联盟组合{WS},{LD, ED}的非合作博弈模型如下:
(18)
求解该非合作博弈问题,可得系统供应商、本地和外地分销商联盟的均衡利润分别为:
(19)
(20)
(2) 局部联盟组合{WS, LD},{ED}的非合作博弈模型
跨流域调水供应链局部联盟组合{WS, LD},{ED}非合作博弈决策次序为:系统供应商和本地分销商组成的联盟首先决策本地终端水价和外地水资源批发价
和
,进而,外地分销商决策终端水价
,则有局部联盟组合{WS, LD},{ED}的非合作博弈模型如下:
(21)
求解该非合作博弈问题,可得系统供应商和本地分销商组成的联盟以及外地分销商的均衡利润分别为:
(22)
(23)
(3) 局部联盟组合{WS, ED},{LD}的非合作博弈模型
跨流域调水供应链局部联盟组合{WS, ED},{LD}非合作博弈决策次序为:系统供应商和外地分销商组成的联盟首先决策外地终端水价和本地水资源批发价
和
,进而,本地分销商决策终端水价
,则有局部联盟组合{WS, ED},{LD}的非合作博弈模型如下:
(24)
求解该非合作博弈问题,可得系统供应商和外地分销商组成的联盟以及本地分销商的均衡利润分别为:
(25)
(26)
3.3. 跨流域调水供应链大联盟优化模型
跨流域调水供应链大联盟组合{WS, ED, LD}情形下,大联盟决策同时决策本地和外地的终端水价
和
,则有联盟组合{WS, ED, LD}的优化模型如下:
(27)
求解该优化问题,可得本地和外地均衡终端水价和订购量分别为:
(28)
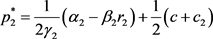 (29)
(29)
(30)
(31)
系统供应商、本地和外地分销商组成的联盟的最优利润分别为:
(32)
4. 跨流域调水供应链合作博弈模型
在前述非合作博弈与优化模型构建与分析基础上,分别构建基于核仁、弱核仁、比例核仁方法以及Shapley值法的跨流域调水供应链合作博弈模型。其中,核仁、弱核仁和比例核仁方法衡量的是不同联盟组合所能带来的福利,体现的是同情与保护弱势群体的平均主义。Shapley值法强调边际贡献,是将收益按照参与人的边际贡献率进行分摊,参与人分配所得收益为该参与人对他所参与的所有联盟组合边际贡献的平均值,体现的是功利主义的公平思想。
4.1. 基于核仁方法的合作博弈模型
定义跨流域调水供应链中的主体集合
,
,主体集合
是一个联盟,
被称为大联盟。
为对大联盟
的一个分割,且对于任意的
,满足
,
。
代表联盟
的特征函数,表示联盟
参与人相互合作所能得到的总效用,而联盟若以个体形式存在,则每个主体的效用分别为
、
和
。定义
,相应的配置分别为
、
和
,则配置向量可表达为
,每个主体在合作中获得的得益(payoff)分别为
、
和 ,则得益向量可表达为
,该得益向量被看成是合作博弈的分配集(imputation),且满足个体理性、集体理性和共同效率 [20] [21] 。令
,则有如下约束条件:i) 个体理性,
;ii) 集体理性,
;iii) 共同效率,
。
,则得益向量可表达为
,该得益向量被看成是合作博弈的分配集(imputation),且满足个体理性、集体理性和共同效率 [20] [21] 。令
,则有如下约束条件:i) 个体理性,
;ii) 集体理性,
;iii) 共同效率,
。
根据合作博弈的相关理论,我们设定如下参数:
,
,
,
,
(1) 核仁模型
定义净福利剩余
,若
,可理解为对参与主体的补贴,若
,可理解为对参与主体的税收 [20] [24] [25] [26] 。通过这样的设定,使得所有的子联盟(但不包括大联盟)获得补贴或支付税收,则存在一个核配置
,使得
最小,则有如下计算核仁(Nucleolus)的线性规划问题:
(33)
(2) 弱核仁模型
定义净福利剩余
,则有如下计算弱核仁的线性规划问题:
(34)
(3) 比例核仁模型
定义净福利剩余
,则有如下计算比例核仁的线性规划问题:
(35)
4.2. 基于Shapley值方法的合作博弈模型
1953年,Shapley提出了合作博弈中合理分配的Shapley-Value理论 [27] ,该理论是合作博弈理论中的一种解的概念,它实现了联盟总体利益在各成员之间的公平和有效的分配。在Shapley值法中,联盟
中每个成员得益分配称为Shapley值,计算公式如下:
,
(36)
其中,
是联盟
中的成员数,
为联盟
中除去成员
后的得益。
5. 数值分析
某跨流域调水工程,本地和外地多年平均降水量
和
分别为1020.6亿m3和1067.5亿m3,设定本地和外地终端用户降水利用率
和
均为0.001,系统供应商和外地分销商降水利用率
和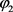 均为0.001;另据调水
均为0.001;另据调水

Table 1. Numerical analysis of non-cooperative game and cooperative game of IBWT supply chain
表1. 跨流域调水供应链非合作博弈与合作博弈对比数值分析
注:价格单位:元/m3,水量单位:亿m3,利润单位:亿元。
工程的经验数据及相关成本核算研究,抽水成本一般介于0.2~0.5元/m3之间 [28] ,假设系统供应商抽水成本
为0.2元/m3,本地分销商和外地分销商的调水成本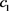 和
分别为0.3和0.4元/m3;设定本地和外地水市场规模
和
分别为20亿m3和30亿m3,本地和外地水资源需求关于价格变动的敏感程度
和
和
分别为0.3和0.4元/m3;设定本地和外地水市场规模
和
分别为20亿m3和30亿m3,本地和外地水资源需求关于价格变动的敏感程度
和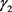 分别为5。本文分别从非合作博弈及合作博弈两个视角对跨流域调水供应链进行数值分析,计算结果如表1所示。
分别为5。本文分别从非合作博弈及合作博弈两个视角对跨流域调水供应链进行数值分析,计算结果如表1所示。
数值分析结果表明:(1) 基于核仁、弱核仁、比例核仁方法和Shapley值方法的合作博弈情形下终端水价低于非合作博弈情形,水资源订购量高于非合作博弈情形。(2) 基于核仁、弱核仁、比例核仁方法和Shapley值方法的合作博弈下跨流域调水供应链及其成员的运营绩效均不低于非合作博弈情形。(3) 非合作博弈下,系统供应商获得的均衡利润高于本地分销商和外地分销商;基于核仁、弱核仁、比例核仁方法和Shapley值方法的利益分配方案下,系统供应商获得的利润同样高于本地分销商和外地分销商。(4) 合作博弈情形中,基于核仁方法和弱核仁方法的供应链利益分配方案完全一致,Shapley值方法与核仁、弱核仁方法相比,系统供应商分配到较多的利润,而外地分销商分配到相对少一些的利润。(5) 基于比例核仁方法的跨流域调水供应链利益分配方案下本地分销商的利润与非合作博弈情形相等,本地分销商处于加入联盟和离开联盟的临界点。
6. 结论
跨流域调水工程运营中往往缺乏有效的合作运营机制,导致参与主体与工程整体的运营目标相偏离。论文从非合作博弈视角和合作博弈视角,分别构建了不同联盟组合下跨流域调水供应链非合作博弈模型、基于核仁方法和Shapley值方法的跨流域调水供应链合作博弈模型,并进行了对比数值分析,在此基础上,探讨了跨流域调水供应链合作运营机制。研究结果表明:(1) 基于核仁、弱核仁、比例核仁方法和Shapley值方法的合作博弈情形下终端水价低于非合作博弈情形,水资源订购量高于非合作博弈情形。(2) 基于核仁、弱核仁、比例核仁方法和Shapley值方法的合作博弈下跨流域调水供应链及其成员的运营绩效均不低于非合作博弈情形,实现了参与各方利益的帕累托改进。(3) 非合作博弈下,系统供应商先决策,具有“先动优势”,获得的均衡利润高于本地分销商和外地分销商;而合作博弈进行利润分配时,是以非合作博弈情形下的利润作为参考点,因此,基于核仁、弱核仁、比例核仁方法和Shapley值方法的利益分配方案下,系统供应商获得的利润同样要高于本地分销商和外地分销商。(4) 相比于非合作博弈情形,基于比例核仁方法的供应链利益分配方案下本地分销商的利润并没有改善,且系统供应商与外地分销商结成联盟对本地分销商不构成威胁,本地分销商有可能会离开联盟,故基于比例核仁方法的跨流域调水供应链利益分配方案下的合作联盟不稳定。(5) 合作博弈情形中,基于核仁方法和弱核仁方法的供应链利益分配方案完全一致;Shapley值方法与核仁和弱核仁方法相比,系统供应商分配到较多的利润,而外地分销商分配到相对少一些的利润。显然,基于核仁方法和弱核仁方法的供应链利益分配方案体现的是更加平均主义的思想,为跨流域调水工程提供了一种更为公平的合作运营机制;而基于Shapley值方法的供应链利益分配方案体现的是功利主义原则,为跨流域调水工程提供了一种更为高效的合作运营机制。总之,基于核仁方法、弱核仁方法和Shapley值方法的合作博弈相比于非合作博弈来说,一方面使得跨流域调水供应链成员有经济动因加入大联盟并稳定地留在联盟内,实现合作水资源定价和定量,另一方面又使得供应链成员合作后获得的剩余利润能够公平地进行配置,有助于提高跨流域调水供应链及其成员的运作绩效,实现帕累托改进。该研究对跨流域调水工程优化运营管理的理论和实践有一定的理论意义和应用价值。
基金项目
国家自然科学基金资助项目(71603125, 71433003, 71301078, 71502085);江苏省高校自然科学研究基金面上项目(15KJB110012);江苏省高校哲学社会科学研究基金资助项目(2014SJB094);中国博士后科学基金面上资助项目(2014M551623);江苏省博士后科研资助计划项目(1301077C)。