1. 引言
日常生活中的决策问题大多具有重复的特征,人们经常要在相同或相似的情境下做出选择。比如开车时决定是否系安全带,企业决定是否在年度税务报告中做“手脚”,医生根据相似的症状诊断病情。在上述问题中,理性的决策者应当总是采取最优化策略评估不同选项的期望效用,因而当一名司机认为系安全带对降低事故死亡率的利大于弊(比如带来的不便)时,他应当始终采取系安全带的措施。然而大量的实证研究表明,人类决策者在面对上述问题时,并不总是能够始终做出对自身有利的选择。
1.1. 概率学习与匹配概率行为
在经典的概率学习任务中,被试需要对两个互斥的随机事件进行重复多次的预测,比如猜测红绿两只灯泡哪只会亮。每次预测中,红和绿出现的概率分别为0.3和0.7,概率值在整个实验过程中保持不变。在上述问题中,始终猜测绿色是更有利的策略,称为最优化。研究者发现,被试在面对上述问题时决策者并没有采取最优化策略。相反,他们倾向于根据事件发生的概率匹配他们的预测,大致以3:7的比例猜测红色和绿色,这一策略或行为模式命名为匹配概率(probability matching, PM) (Vulkan, 2000)。
1.2. 匹配概率的两种假说
关于匹配概率行为的心理机制存在一定的争议,前人的研究主要有支持两种假说。首先,联结学习假说认为,PM行为主要来自于外插(顺应)短期频率经验的简化策略(Erev & Barron, 2005; Myers, 1976)。假如决策者在记忆窗口中估计事件出现的频率,近期内某一事件越多,就更倾向于预测该事件会再次发生,较小的记忆容量导致较高的估计误差,使得反应行为偏离最优。其次,模式搜索假说同样认为决策者会追溯短期的经验,只不过他们在努力寻找随机过程中存在的规律(Gaissmaier & Schooler, 2008; Plonsky et al., 2015)。由于被试努力探索的规律根本不存在,模式搜索策略也必然导致次优的PM模式。总之,匹配概率行为可能来自两种相互独立的认知过程。
一些研究者尝试通过操纵认知负荷和认知能力两个变量对区分这两种过程(见表1),其基本假设如下。首先,增加认知负荷(比如双任务操纵)会剥夺短时记忆资源,因而依赖于短期经验的联结学习假说预测PM会增加,因为记忆容量更小,频率估计更不准确;认知负荷会干扰模式搜索的过程,因而如果PM来自探索模式的过程,认知负荷应降低PM行为。其次,对于认知能力和短时记忆容量,联结学习假说预测,记忆容量更高的个体频率估计更准确,因而PM行为降低;由于高记忆容量更加方便被试探索规律,模式搜索假说预测记忆容量和PM行为的正相关。
通过对以往研究进行总结,我们发现以往的研究结论中存在诸多不一致性(见表2)。首先,的确有证据支持认知负荷会增加PM行为。比如当同时存在的语言工作记忆任务占据了短时系统的加工能力,最优化反应倾向平均增加了5%~10% (Wolford et al., 2004),另一项利用葡萄糖剥夺造成认知损耗的操纵也发现了相同的结论(McMahon & Scheel, 2010)。但是这一结论并没有被后续的研究者重复,比如Otto等人(2011)并没有发现双任务操纵对任务绩效的影响(Otto et al., 2011)。实际上,当实验控制了最优化和PM两种反应模式需要的认知努力后(排除了启发式的解释),一些研究者的确观测到与联结学习假说更一致、与模式搜索假说相悖的证据(Schulze & Newell, 2016),即认知负荷增加PM。但是该结论只在特殊的任务条件下才成立,因而不具有一般性。
导致这些不一致性的主要原因可能有以下几点。首先,认知能力和PM行为之间的相关性可能是一个非常间接的证据,因为认知能力可以通过很多不同的途径——比如年龄、智力、认知努力和认知策略——影响重复预测任务中被试的行为绩效(Stanovich & West, 2008)。其次,双任务操纵中,实验者使用的干扰任务存在差异(Wolford et al., 2004; Schulze & Newell, 2016; Otto et al., 2011),对儿童使用的较为特殊的任务形式(Denison et al., 2013)。此外,认知负荷与认知能力、策略之间的交互作用进一步增加了结果的复杂性。比如张玉婷(2010)的实验采用双任务设计,并通过指导语直接操纵了策略:一组被试的任务被描述为赌博,要求他们凭借直觉进行预测(单纯匹配组);另一组的任务被描述为解决问题,要求他们通过仔细分析尽可能提高正确率(分析匹配组)。结果发现相对于单纯匹配组,双任务操纵对分析匹配组的影响更大;也就是说认知损耗只对那些努力寻找规律的被试起作用,能够显著提升他们的任务绩效(张玉婷,2010)。总之,以往研究中存在的变量混淆,可能是导致无法区分概率学习的两种认知过程的主要原因。
1.3. 实验设计和假设
本研究尝试从相反的角度出发,不是剥夺认知加工资源,而是通过利用动态反馈窗口这一外部辅助手段拓展记忆容量。我们注意到,两种学习过程都依赖于短时记忆系统对近期事件的追溯。二者不同之处在于,联结学习过程需要追溯事件的频率,因此预测连续出现同一事件会增加被试预测该事件的倾向,即正近因效应(positive recency effect);相反基于赌徒谬误(gambler’s fallacy)信念的模式搜索策略会导致负

Table 1. Explanations and predictions of two different hypotheses of PM
表1. 两种假说的行为解释及预测

Table 2. Summary of evidences from cognitive load/ability manipulation
表2. 认知负荷/能力证据汇总
近因效应,即预测与连续事件相反的事件。鉴于此,我们提出如下三个假设。
假设一:基于连续事件的近因曲线应反映出正近因和负近因效应的叠加。
假设二:对近期事件敏感的行为模式受窗口容量的调节;窗口容量越高,负近因效应(赌徒谬误)越强。
假设三:随着重复经验次数的增加,行为模式逐渐向正近因趋近;即早期的PM行为更多来自模式搜索策略,后期则主要反应了联结学习过程。
2. 方法
2.1. 被试
选取西南大学的50名大学生样本(26名男生,24名女生),年龄范围在18~25岁之间(平均年龄21.2岁)。被试皆为右利手,没有精神方面的疾病,视力或矫正视力正常,且未修过概率、统计学方面的课程。实验结束后,被试根据其任务绩效被试获得12~14元的报酬。
2.2. 任务
程序由Matlab的Psyhotoolbox编写,任务背景被描述为一个猜灯泡游戏:被试需要预测屏幕中央灯泡的颜色,正确的预测可获得金钱奖励,屏幕上方的动态反馈窗口更新近期的事件,如图1所示。任务分8个阶段(Block)进行,每个阶段50个试次,两个阶段之间有30秒的休息时间。每个试次开始时,屏幕中央显示“请选择”提示语,被试用鼠标点击红色和绿色按钮,1秒钟后呈现反馈。反馈包括三个部分:1) 金属盒子的中央显示出灯泡的颜色,与灯泡颜色一致的选择可获得奖励;2) 奖励金额在屏幕下方的总收益显示框(图中未显示)中被更新。3) 上方的动态窗口中更新事件,窗口从右往左滚动,最右侧为最近出现过的事件。反馈的呈现的时间为1.5秒,接着屏幕中央再次显示“请选择.”,进入下一个试次。指导语规定试被必须在5秒钟内做出选择,假如5秒钟后被试仍未做出选择,电脑会随机替被试选择一种颜色(平均有1.8%的试次属于这种情况,在数据分析中这些试次被剔除)。
2.3. 变量的操纵和控制
实验考察短时记忆容量对模式搜索行为的影响,通过操纵动态反馈窗口的容量实现对记忆的辅助作

Figure 1. Sketch of the task (length 9 condition)
图1. 任务示意图(容量9条件)
用。采用单变量被试间设计,被试被随机分配到两个条件(每组25人),容量3条件下窗口中更新最近的三次事件,容量9条件下窗口中更新最近的9次事件。因此,实验通过操纵动态窗口容量人为制造了两种条件下短时记忆容量的差异(分别为3和9)。
灯泡颜色序列由完全随机的伯努利过程生成,其中一种颜色为高概率事件H (出现的概率为0.65,低概率事件为L),高概率事件的类型(红或绿)以及红绿按钮的位置(左和右)在被试间进行随机化的处理。奖励的规则如下:在进行任务前,总收益显示框中的初始金额为¥5,每一次正确的预测可获得额外的¥0.3的奖励。假如被试在400次预测中有300次正确,其总收益为5 + 0.3 × 300 = 14元。正式实验开始前,被试进行10个试次的练习,目的是熟悉任务程序。10个练习试次对所有被试采用相同的序列(H-L-H-H-L-H-H-H-L-L-H为高概率事件)。
2.4. 问卷
采用自制的问卷,实验结束后要求被试进行填写。问卷主要包括以下几个部分:1) 估计事件出现的频率;2) 询问被试的策略使用情况以及策略认同(比如“你使用了怎样的策略?”“你认为哪种策略更好?”);3) 询问被试是否发现序列中存在的模式规律,如果有则要求他们写下他们所认为的规律。
2.5. 数据分析
描述统计量:感兴趣的因变量包括:1) 选择率R(H) = 选择H事件的频数/总选择次数;2) 切换率(switch rate, SR) = 选择切换频数/总选择次数,其中选择切换频数指被试在某一个试次中的选择不同于上一个试次的选择的所有试次的总数;比如对于长度为6的选择序列HHLHHL,其切换频数为3 (总共改变了三次),因而切换率为3/6 = 0.5。一般认为,切换率可能反应了不确定状况下的探索行为。3) 近因率(recency rate) = 近因频数/总选择次数。近因频数指第t次选择和第t-1次事件相同的次数。一般认为,近因率部分反应了联结学习的效果律,取值越高说明被试越倾向于重复最近一次成功的选择/回避失败的选择。4) 反应时。5) 正确率。
近因曲线:近因曲线反应了对连续事件敏感的行为模式,可用于区分联结学习和模式搜索假说(Plonsky et al., 2015)。根据联结学习假说,连续出现相同事件应当增加被试预测该事件的倾向,即预测行为应服从正近因效应(positive recency effect)。因而当以连续出现高概率事件H的次数为横轴,高H事件的选择率为纵轴,画出近因曲线时,联结学习假说预测该曲线呈递增趋势。相反,假如被试使用“老练”的找规律的策略,可能会在连续出现相同事件后更倾向于预测相反事件,导致递减的近因曲线(负近因效应) (Boynton, 2003),而找规律的主要原因可能来自赌徒谬误错觉。联结学习和赌徒谬误效应是可以共存的,因而近因曲线可能呈现出复杂的“波浪”形态(Altmann & Burns, 2005; Boynton, 2003; Plonsky et al., 2015)。此外,一些研表明学习会影响赌徒谬误效应(Edwards, 1961)。根据前人的研究结论,我们尝试提出如下假设:1) 拓展事件记忆会导致负近因效应,且负近因效应随窗口容量的增加而增加;2) 近因效应和学习效应之间存在交互作用,实验早期阶段窗口容量对负近因效应的影响大于晚期。
3. 结果
3.1. 描述统计量
如表3所示,被试对概率值的主观估计较为准确,容量3和容量9条件下平均估计值分别为0.673 (sd = 0.07)和0.685 (sd = 0.08)。与真实值0.65相比,有略微高估的倾向,这与前人结论相一致(Otto et al., 2011)。操纵窗口容量并没有影响组水平的行为模式,所有因变量的组间差异均未达到显著水平。
3.2. 近因效应
图2为早期阶段的近因曲线,对连续事件敏感的行为模式在不同窗口容量条件下存在差异。从图中可以看到,随连续出现H (高概率)事件次数的增加,两种条件下近因曲线均呈现出先增–后减–再增的“波浪”形态,这与前人的结论相一致(Altmann & Burns, 2005; Plonsky, et al., 2015)。但是在两种条件下被试的近因模式存在一定的差异:相对于容量3,容量9的条件下负近因效应持续的时间更长;递减趋势由连续3次H事件开始,直到超过8次后才开始“回升”,前者则在第5次后就“回升”(7和8处的t值分别为2.53和3.82,通过了Bonferroni校正)。此外,在小概率事件L的部分,容量9条件下显示出顺应“趋势”倾向,即H选择率随连续L次数增加递减;容量3条件则显示出复杂的“U”型,当连续L少于5时顺应“趋势”,超过5后则出现了逆转,H选择率增加(“−5<”处t值为3.66)。这些结果表明,拓展记忆的操纵能够改变预测行为的近因模式,尤其是于赌徒谬误有关的负近因效应。
通过比较早期(图2)和后期(图3)的近因曲线可以发现,负近因效应在实验的后期阶段明显有减弱的迹象;尤其对于容量9条件,在H连续出现4-8次时,原先的的递减模式几乎完全被递增所取代(除了7、8处有少量递减迹象)。此外,早期阶段两种条件近因模式的差异在后期阶段也几乎完全消除了,暗示学习效应和近因效应间的交互作用。
3.3. 策略分组
根据问卷测量的策略使用情况对被试进行分组:声称发现规律(比如“和最近3个的中间那个一样或者和多的那个一样。”,“五个绿色后有1红色再两个绿色后有2红色,找规律,有循环。”)的被试(探索者)有28人,剩下的22人为非探索者。
为了考察学习效应,我们对选择率进行3(分组) × 8(阶段block)的重复测量方差分析(r-ANOVA)。分析结果显示(如图4所示),选择率的学习效应显著(F(7,375) = 21.6; p < 0.01)。分组效应显著(F(2,375) = 14.3; p < 0.01),

Table 3. Mean(SD) of descriptive statistics at group level
表3. 组水平描述统计量的均值(标准差)
与探索者相比,非探索者更倾向于使用最优化的策略。此外,分组和任务阶段的交互作用达到了显著水平(F(14,375) = 2.21, p < 0.05),暗示非探索者的学习曲线更陡峭,习得最优化策略的速度更快。此外,切换率等其它因变量也显示出类似的模式。该结果与前人的研究结论相吻合(Unturbe & Corominas, 2007; Yellott, 1969),即声称发现随机过程中复杂规律的被试更倾向于采用次优的匹配概率策略。
4. 讨论
本研究的主要结论总结如下。我们发现正近因效应和负近因效应同时存在于对近期事件敏感的行为

Figure 2. Recency curve in late period (1~200 trials) of the experiment
图2. 实验早期(1~200试次)的近因曲线

Figure 3. Recency curve in late period (201~400 trials) of the experiment
图3. 实验后期(201~400试次)近因曲线
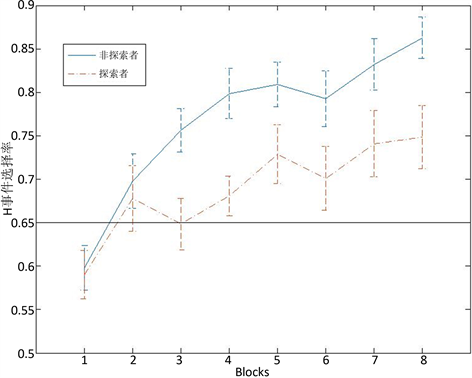
Figure 4. Learning Curve of explorer and unexplorer
图4. 探索者(组)和非探者的学习曲线
模式,“波浪型”的近因曲线暗示联结学习和模式搜索过程的共存:追溯事件频率的联结学习策略(导致正近因效应),基于赌徒谬误信念的模式搜索策略(导致负近因效应)。有趣的是,在连续出现多次(3~8次)高概率事件H时,被试在长窗口条件下表现出更多的负近因效应;但是在连续出现多次(5次以上)L事件时却出现了相反的模式,即短窗口条件的负近因效应更高。
4.1. 情境敏感的编码策略
这一行为模式可以由记忆编码过程解释。人们会根据外部环境使用不同的认知编码策略,编码策略又会进一步对再认、推论和预测行为产生影响(Altmann & Burns, 2005; Plonsky, et al., 2015)。在本研究所使用的任务中,当不存在任何记忆辅助设备(无反馈)时,多数人可能会对次数超过一定数量(比如5)的连续事件编码为同一种类型,也就是说,没有必要对连续5次和5次以上事件进行更详细地区分(或者说记忆能力不足以支持他们对较长的连续事件的次数进行准确的编码)。本研究并未发现近因曲线在无反馈条件和容量3条件中存在任何差别(前人的研究也提供了类似的证据(Carlson & Shu, 2007)),这在一定程度上支持了上述假说,因为窗口容量没有达到记忆的上限,不足以影响编码策略。也就是说,在短时记忆容量受约束的条件下,使用泛化高次数连续事件的编码策略能够节省认知资源;相反,当外部辅助设备提供的容量超过短时记忆的阈值上限后,这种认知俭省的编码策略则显得没有必要。借助外界设备,在容量9条件下被试能够对每一种连续事件的模式(次数)进行准确的编码。
编码策略通过再认和推论影响预测行为,导致波浪形的近因曲线(Altmann & Burns, 2005; Plonsky, et al., 2015):1) 当连续事件的次数在编码上限之内时,被试会通过线索再认(提取经验中不同次数的条件概率)、或是直接采用赌徒谬误的策略预测相反的事件;2) 当连续事件次数超过编码上限后被试推测环境发生了变化,于是顺应趋势。这就是为什么在无反馈和容量3条件下,编码上限(假如为5)使得负近因效应只能维持在3~5范围内,超出5就会出现回升;反之在容量9条件下,曲线的负近因(递减)区域被拓展(直到8处才出现回升)。此外,对于曲线连续出现L事件的那一端,两种条件的分离同样出现在5处,因而我们推测被试的编码上限大致为5。总之,窗口容量的操纵改变了被试的编码上限,并通过影响编码和推论策略造成了近因曲线的差异,该结果在一定程度上支持了模式搜假说。
此外,我们发现窗口容量和学习效应之间的交互作用:两种条件下近因曲线的模式在实验的早期阶段差异更大,后期则不存在差异;此外,随着重复次数的增加,曲线的负近因(递减)部分逐渐被正近因(递增)取代。该结果暗示可能存在行为模式的转变:由的早期模式搜索策略向后期的联结学习策略过度。
4.2. 情境效应与行为适应性
实际上,情境效应本身也是一个有趣并值得探索的问题。因为在不同反馈条件下,决策者面对的随机过程是完全相同的,情境敏感的行为模式可能反应了某种错觉。之前的研究发现,外部线索可以改变决策者对随机过程持有的信念(Green et al., 2010; Schul et al., 2007);更一般地讲,控制错觉可以看作是表征策略的误用,即将适应于其它(非随机)情境的心理表征错误地迁移到给定的(随机)任务中。就预测效度来讲,本研究的动态窗口中提供的信息完全没有任何价值,然而决策者的确表现出环境敏感的行为模式,且充分学习并没有完全消除条件间的差异。未来的研究者可顺着本文的思路操纵心理表征,诱导更多的错觉。
从相反的角度看,环境敏感的行为可能反应了利用(exploit)环境统计规律的适应性策略。比如本实验在中决策者能够采用适应事件窗口容量的编码策略,假如环境中的确存在基于连续事件次数的条件规则,这种编码策略有助于决策者发现规则。未来的研究应当更多地关注认知能力和任务环境的交互作用。比如认知负荷操纵可能在某些条件下降低任务绩效,而在另一些条件下提升任务绩效;此外,额外的反馈和信息也并非总是会带来有利的行为后果。未来的研究应尝试界定上述条件。
值得注意的是,我们并没有在组水平发现窗口容量对选择率的影响,这似乎与我们的预期不符。一种可能的解释是,对整组被试取平均的分析方法掩盖了个体水平的一些重要信息;当我们改进统计方法,采用基于试次的参数化模型以及基于行为模式的相关分析后,的确得到了一些不同的结论。因此,在解释组水平的效应时应当谨慎,因为基于平均的组统计可能隐藏了个体水平的行为模式的差异。
5. 结论
本研究采用一种全新的窗口反馈操纵,通过对近期事件敏感的行为模式进行分析,成功分离了概率学习的两种认知过程。在对以往的范式进行改进的基础上,为匹配概率行为的两种假说提供了更为直接的证据。
基金项目
本研究得到国家自然科学基金(31400959)、中央高校基本科研业务费专项资金项目(SWU1509422)、中国科学院心理健康重点实验室开放课题基金(KLMH2015G01)和中国基础教育质量监测协同创新中心自主支持课题(2016-06-014-BZK01)的资助。