1. 引言
当今社会,风险影响着经济生活的方方面面,大到影响国家宏观决策与经济发展,小到决定一个公司的生死存亡。无论是在银行,保险公司还是在其他的商业公司中,风险的存在形式多种多样,多个风险之间的相依关系也是错综复杂。因此,对风险实行有效的管理对公司的发展有重要的意义。风险管理的目标就是希望将风险固定下来,及时拿出相应的准备金来应当对风险,若风险度量不准确,则会极大的影响公司的稳定性。
在实际生活中,尤其是在金融行业,风险并不是单独存在的,往往是以多个风险加和的形式存在。此时风险的边缘分布一般已知,当n个风险的分布相互独立时,处理是比较方便的,但在实际中风险之间并非相互独立,并且它们之间的关系,我们也一无所知。那么在风险之间关系未知的情况下,如何使得风险的加和风险最小呢?
2. 风险度量
在研究风险之前,首先我们应该先说明如何度量风险。度量风险的测度有很多,例如:VaR,ES,TVaR,CTE等 [1] ,它们的定义如下:
定义2.1. VaR (Value-at-Risk) [2] [3] 对于风险S,在(置信)水平p下的VaR定义为:
因此,VaR恰好是在p点计算的S的分布函数的反函数。
定义2.2. ES (expected shortfall) [4] 对于风险S,在水平
时的期望缺口(ES)定义为:
定义2.3. VaR (Tail-Value-at-risk)对于风险S,在水平
时的TVaR定义为:
从上述表达式可以看出,TVaR恰好是S从p开始的VaR的算术平均。
定义2.4. 条件尾期望(Conditional Tail Expectation) (CTE)对于风险S,在水平
时的条件尾期望定义为:
因此,CTE为“在最坏的
情形下的平均损失”。
在众多的风险度量方法中较为常用的为VaR和ES,因为VaR有比较直观的含义,它相当于是随机变量的分位数,也就是说损失随机变量大于其
分位数最大为( )的概率,而且VaR是可以回测的。ES风险度量是尾部VaR的平均,它一般比VaR的值偏大,所以它是一个比VaR更为保守的风险测度,而且它是一个次可加的风险度量,但由于ES计算的是VaR的尾部平均,因此ES的计算与VaR相比更加困难,甚至是不可能的。近二十年间对VaR的研究比ES更多,而且对VaR的统计估计更为成熟,银行、保险公司等金融机构也更多的用VaR作为其风险度量。本文将针对其中的一个风险度量,即VaR进行研究。VaR早在1993年由G30集团在研究衍生品种基础上发表《衍生产品的实践和规则》提出,后来在风险管理方面得到了广泛应用 [5] 。
)的概率,而且VaR是可以回测的。ES风险度量是尾部VaR的平均,它一般比VaR的值偏大,所以它是一个比VaR更为保守的风险测度,而且它是一个次可加的风险度量,但由于ES计算的是VaR的尾部平均,因此ES的计算与VaR相比更加困难,甚至是不可能的。近二十年间对VaR的研究比ES更多,而且对VaR的统计估计更为成熟,银行、保险公司等金融机构也更多的用VaR作为其风险度量。本文将针对其中的一个风险度量,即VaR进行研究。VaR早在1993年由G30集团在研究衍生品种基础上发表《衍生产品的实践和规则》提出,后来在风险管理方面得到了广泛应用 [5] 。
3. 完全混合及相依结构
在问题开始之前,首先给出相关定义。
3.1. 完全混合
是一个正整数,对于一个R上的概率分布F,如果存在
个随机变量
使得
是一个常数,则称分布F是
阶可完全混合的(或简称为
阶可混合)。其中
的联合分布成为一个
阶可混合结构 [6] ,(n-complete-mix)。
Sklar (1959)指出可以将随机变量的联合分布分解成边际分布和它们之间的相依结构(copula),而变量之间的相依结构可以用copula来表达 [7] ,下面给出copula函数的定义。
假设
联合分布函数
,其边际分布函数分别为:
,
均服从
上的均匀分布,则
的联合分布就称为copula。
根据定义
令
,我们可以得到
3.2. 同单调与反单调
3.2.1. 同单调
假设随机变量
是概率空间
上的随机变量,如果对任意的
,有
,则称二维随机变量X,Y同单调。
3.2.2. 反单调
二位随机变量(X, Y)为反单调的,如果(X, −Y)是同单调的。
3.3. 完全混合的性质和例子
在给出上述的定义后,我们给出完全混合的性质及几个完全混合的例子。
3.3.1. 完全混合的性质
1) 完全混合仿射变换下的不变性
假设随机变量
的分布是n
阶可混合的,那么对于任意常数a,b,随机变量
的分布也是n
阶可混合的。
2) 完全混合分布角度的加性
假设随机变量
和
,F和G均可以n
阶混合,并且拥有一致的中心
,则对于任意的
,有
是n阶可混合的,并且拥有一致的中心
。
3) 完全混合指数角度的加性
若随机变量
的分布是n阶可混合的,也是k阶可混合的,那么对于任意常数a,b,F也是(an + bk)阶可混合的。
4) 完全混合的收敛性 [8]
假设分布F和
都是紧集
上的分布,
都是n阶可混合的,
,并且当
时,
依分布收敛于F,则F一定是n阶可混合的。
3.3.2. 完全混合的例子
1) 均匀分布的n(n ≥ 2)阶可混合性
假设随机变量X服从
的均匀分布,根据仿射变换的性质,我们可以将X变换为
的均匀分布,所以不失一般性,仅讨论
是否可以n阶可混合即可。
显然,对称分布一定是2阶可混合的,假设
,一定存在某常数b,使得
,此时
,说明Y是2阶可混合的。因为
也是对称分布,所以
也是2阶可混合的,所以
所有偶数阶均是可混合的。接下来,只需证明
是奇数阶可混合的。
首先我们考虑是否能够三阶可混合。考虑
,当
,
,
;当
时,令
,
,此时
均服从
的均匀分布,
a.s.,因此,
是三阶可混合的,又因为它是2阶可混合的,所有大于1的正整数均可由2,3的组
合进行构造,所以,
是可以n阶可混合的,由此,根据仿射变换,
也是可以n阶可混合的。
2) 正态分布的n(n ≥ 2)阶可混合
单峰对称分布可表示为一族均匀分布的凸组合,而由(1)可知,所有均匀分布均是可n阶混合的,根据完全混合分布角度的可加性,单峰对称分布均可以n阶混合。正态分布也属于单峰对称分布,所以正态分布是n阶可混合的。
除此之外二项分布也可以完全混合,在这里不再详述,还有一些分布永远无法混合,比如指数分布、几何分布、负二项分布、泊松分布等,因为这些分布均为一端有界而另一端无界,由于此时重心靠近一端,而另一端的极值无法永远无法与另一端混合形成混合结构,因此这些分布用于无法完全混合。
接下来我们从完全混合问题的经典问题入手,即
,相依结构未知,如何使得下式最小:
在两个随机变量(n = 2)时比较好考虑,当两个随机变量反相关(当一个随机变量增大时,而另一个随机变量减小)时,两随机变量加和为常数,此时两随机变量加和的方差达到最小,也就是构成了完全混合结构。但若n
个随机变量,则无法使得随机变量之间两两反相关,这类似于负负得正,那如何设计出一个相关结构使得方差最小呢?最理想的情况就是当n个随机变量加和为常数,即形成混合结构时,方差达到最小,为0。完全混合能够使得各随机变量间达到较好的反相关性,因此在考虑下述问题时,我们首先考虑完全混合。
4. 风险加和的VaR最小值问题
4.1. 问题相关定义和引理
4.1.1. 质量函数
质量函数是每个点上的质量,这类似于密度函数,与密度函数唯一不同的是质量函数不要求其和为1。
4.1.2. 引理
上的一个质量函数A满足质量递减,且重心为0,则A一定是 阶可混合的。其中
表示的是质量函数A的点集,
阶可混合的。其中
表示的是质量函数A的点集,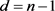 ,
中有
个点。
,
中有
个点。
引理的证明见文献 [8] 。
4.1.3. 推论
假设分布P概率密度函数p(x)在
是单调的,并且在
之外的地方
,如果p(x)是单调
递增的,并且有
;如果p(x)是递减的,并且有
,则P对于任意大
于等于n可混合。
4.1.4
或
(n为正整数),密度函数为p(x)在区间
上,在区间
以外有
,
相依结构未知,
,在置信度为
时,能否使得
最小或最大,使得下式成立的相依结构是什么?
或
因为我们考虑的是VaR,只需要将区间
上的值进行搭配,而不需要考虑区间
上的值,所以后续讨论我们只针对区间
进行讨论,并记此区间上的随机变量的分布函数为F (具体只需进行归一化即可),因此在新的分布下,上述问题等价于
。
我们首先考虑p(x)单调递减,当
时,分布F的密度函数p(x)在区间
上单调递减,其期望
。当
时满足条件的分布F是不存在的。当
时,满足条件的分布只有均匀分布
,
根据上述完全混合的例子中可以看出,这是2阶可混合的。
当
时,首先令
,在
上
,其均值为0,密度函数单调递减。令
为[NY]/N的分布函数,其中[NY]为NY的整数部分,{NY}表示NY的小数部分,
为
上的离散均匀分布的分布函数。由于
且
,所以其期望也在
之间,因此
。
由于
服从
上的离散均匀分布,因此其均值为:
因为
,即
,所以上式
。
接下来,我们想寻找一个
,构造一个 和
的组合,使组合的期望为0,取
和
的组合,使组合的期望为0,取
构造函数
,则
,且
在
上递减,因而
可
阶可混合。
当
时,根据完全混合的收敛性知,
依分布收敛于F,且F是
阶可混合的。
根据完全混合的仿射不变性,我们可以得到当密度函数p(x)在区间
上单调递减,在区间
以
外有
,且
时F可n阶完全混合。
由于当X的密度单调递增时,−X的密度则单调递减,若X可完全混合,由完全混合仿射不变性可知,−X也可以完全混合,故密度函数单调递增也可完全混合。
当
时,无法构成完全混合结构,我们考虑以下的结构:
当均值条件不满足时,这说明中心偏左,最大值即使用最小的来进行调和也无法达到均值,于是我们考虑将最大的与(
)个最小的匹配,即
配(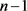 )个
,
,直到
区间内能够混合。下面我们给出该相关结构:
)个
,
,直到
区间内能够混合。下面我们给出该相关结构:
随机向量(
)具有一致的边际分布,则分布函数的联合分布(copula)为
上的均匀分布,即
,其中
为copula结构,它满足:
当密度函数递增时:
(a) 对每一个
,给定
,我们有
;
(b) 对于所有的
,
是一个常数。
令
,其中
为copula
满足(a) (b)条件存在的所有c中的最小值,并且
当且仅当F是n阶完全混合的。定义
,则有
当密度函数递减时:
(c) 对每一个
,给定
,我们有
;
(d) 对于所有的
,
是一个常数。
由于当X的密度单调递减时,−X的密度则单调递增,所以F的性质与密度递增时类似,定义
,则有
下面我们对该结构的存在性进行证明。由于密度函数单调递增时和单调递减时类似,所以我们只针对密度函数单调递增的情况进行证明。
首先我们令
使得
的联合分布均匀的分布在每个线段
。通过4.1.3推论可知存在
使得
是一个常数,因为
的密度单调递增,并且由
可知,
令随机变量U是均匀分布,且与(
)相互独立,且
,则
,
。
的联合分布满足性质(a) (b),这表明
是存在的。
特别地,当n = 2时,如何得到
或
?
当两个随机变量加和时求其最大最小值思路是比较容易想的,因为我们想要让该组合的分位数较小,应该考虑在取值一定的情况下,让他们的加和尽可能的集中,当所有的组合都集中于一点时,
达到了最小,那什么样的相关结构能使他们集中于一点呢?就是反单调的时候,相关结构如图1所示。
对应上述图1中相依结构的表达式为:
该相依结构同时达到了
的最大值和最小值,若取
,则其最大值为1.95,最小值为0.95。

Figure 1. The copula of anti-monotone with two variables
图1. 两随机变量反单调的相关结构
二维情况下比较容易计算VaR的最值,但在多维的情况下就没有那么容易了,具体的计算请参考文献 [9] 。
致谢
首先,我要感谢我的指导老师王彬老师对我的教导。从文章的选题、构思、撰写到最终的定稿,王彬老师都给了我悉心的指导。此外,我还要感谢所有给予我帮助的老师和同学,感谢您们给予我的鼓励和关怀!