基于J函数的含油饱和度建模方法—以陆丰A油田为例

Modeling Method of Oil Saturation Based on J Function—Taking Lufeng A as an Example

摘要: 随着注水开发的进行，油层各项参数随之发生变化。由于水淹的影响，测井解释的含油饱和度与油藏原始含油饱和度在数值和分布上都有显著差异，不能代表油藏的原始分布状态。依据平均化后的毛管压力曲线，分流动单元对各类型储层进行原始含油饱和度的计算，建立基于J函数的含油饱和度模型，减小不同钻井时期测井解释含油饱和度的误差，对储量复算、油藏数值模拟等工作具有重要意义。

Abstract: With the development of water injection, the parameters of the reservoir change accordingly. Because of the influence of flooding, there is a significant difference between the oil saturation of logging interpretation and the original oil saturation of reservoir, and it cannot represent the original distribution of oil reservoir. According to the average capillary pressure curve, the original oil saturation of each type of reservoir is calculated by flow unit, and a model of oil saturation based on J function is established. The error of oil saturation in logging interpretation at different drilling periods is reduced. Therefore, this work is important for reserves recalculation and reservoir numerical simulation.

1. 引言

随着油田注水开发的不断进行，油层的孔隙结构发生改变，含油饱和度发生变化。一般表现为泥质含量下降，孔隙度、渗透率增加以及电阻率的下降。因此，对开发后期的新钻井来说，测井解释含油饱和度不能代表油层原始含油饱和度，建立在测井解释基础上的含油饱和度模型不能代表油藏原始的分布状态。

传统饱和度建模一般基于饱和度解释曲线采用空间插值算法完成，该方法可靠性很大程度上依赖于控制点数量，因此对于原始饱和度建模来说只能用少量的早期未水淹井做为控制 [1] 。而且插值方法无法考虑油水界面及毛管力的影响，无法准确表征油水过渡带。利用毛管压力计算的原始含油饱和度只与储层孔隙结构、油柱高度、油水密度差有关，与电阻率无关 [2] [3] [4] 。基于J函数的饱和度建模方法主要使用受流体影响较小的孔隙度和渗透率属性场，因而控制点数更多。另外，该方法最大的特点是考虑毛细管力所引起的流体过渡带，能够为数值模拟提供近似平衡的饱和度场，更有利于后续的数值模拟研究。

2. 基本原理

2.1. 利用J函数计算原始含油饱和度

油藏形成过程实际上是石油浮力不断克服毛管压力而发生垂向或侧向运移，在遇到遮挡层而在储集岩聚集而成。石油浮力与油柱高度及油水密度差有关，毛管压力则与界面角、接触张力和孔喉结构有关(式1，2) [5] [6] 。两者的相对大小决定了油气是否能进入储层孔隙，也就决定了油藏的原始分布状态(式3) [7] 。

$F_{浮}=\Delta \rho gH$ (1)

$P_c=\frac{2\sigma \cos \theta }{r}$ (2)

当油气充注结束，毛管压力与浮力达到平衡时，有以下关系：

$P_c=\Delta \rho gH$ (3)

式中，F_浮为石油浮力，N； $\Delta \rho$ 为油水密度差，g/cm³； $P_c$ 为毛细管压力，MPa；σ为流体两相的界面张力，mN/m；θ为流体与固体的接触角，˚；r为毛细管半径，μm； $H$ 为油柱高度，m； $P_c$ 为毛细管压力，Mpa。

利用这个基本原理可以根据毛管压力曲线计算油藏的原始含油饱和度。岩块样品的毛管压力曲线只能代表该点上的油藏特征，在实际研究过程中，为了得到整个油藏范围内各类储层条件下的油藏特征曲线，需要对多块岩心样品进行平均化处理。Leverett于1941年提出无因次J函数(式4，5) [8] ，拟合S_wn与J(_Swn)以得到代表各类储层条件的毛管压力曲线，从而实现对原始含油饱和度的计算。

$J_{\left(Swn\right)}=\frac{P_c}{\sigma }\sqrt{\frac{K}{\phi }}$ (4)

$S_{wn}=\frac{S_w-S_{wi}}{1-S_{wi}}$ (5)

式中 $S_w$ ，岩心含水饱和度，%； $S_{wi}$ ，岩心束缚水饱和度，%；K，岩心水平渗透率，mD；φ，岩心有效孔隙度，%。

实际储层中，由于非均质性的影响，一条毛管压力曲线不能代表储层每个点的性质，因此分类前需要根据物性和储集层质量系数指数(I_rq) (式6) [9] 对样品进行分类 [10] 。I_rq可以定性反映储层孔隙结构，I_rq值越大，储层孔隙结构越好，孔喉半径越大。利用I_rq指数分类后，每类样品具有类似的孔隙结构，因此也可以同一毛管压力曲线代表。

$I_{rq}=\sqrt{\frac{K}{\phi }}$ (6)

式中I_rq，储集层质量系数指数，无量纲；K和φ同上。

获得平均毛管压力曲线后，将实验室条件下的毛管压力曲线转变为储层条件下的毛管压力曲线(式7) [11] 。

$P_c\left(res\right)=\frac{{\sigma }_{res}\cos {\theta }_{res}}{{\sigma }_{lab}\cos {\theta }_{lab}}\ast P_c\left(lab\right)$ (7)

式中 $P_c$ ，毛管压力，Mpa；σ，界面张力，dyn/cm；θ，润湿接触角，˚； $P_c\left(res\right)$ 表示油藏条件下的毛管压力值，Mpa； $P_c\left(lab\right)$ 表示实验室条件下的毛管压力测量值，Mpa。

由于平衡时毛管压力与浮力相等，对于已知的任意高度，可以计算其原始含油饱度 [5] 。

2.2. 基于J函数的含油饱和度建模

根据上述理论，在孔隙度、渗透率模型的基础上，结合流体界面深度认识及界面张力、润湿角等参数，可以完成基于J函数的含油饱和度建模。

对于开发成熟的油气田，利用Ｊ函数建立的含油饱和度模型，更符合油气田开发实际，可以更真实地反映出地层的原始含油(气)状态，为储量复算和油藏数值模型提供准确依据。

3. 实例运用

陆丰A油田位于珠江口盆地北部坳陷带，为一平缓、完整的背斜构造。主力油层2500层储层岩性主要为块状砂岩夹泥岩。储层物性好，产量高。岩心分析孔隙度3.6%~26.17%，平均19.16%；渗透率0.2~8843.9 mD，平均134 mD。经过20多年的投产开发，处于特高含水的挖潜后期。

本次研究收集到岩心毛管压力资料共3口井47块。I_rq值为0.11~8.32，按照聚类分析结果将其划分为11类，个别偏离较大的样品会造成J函数拟合相关系数不高，删除后对各类样品进行拟合(图1，图2)，得到11类J函数(表1)。

Figure 1. Capillary pressure curve of the seventh sample

图1. 第7类样品毛管压力曲线

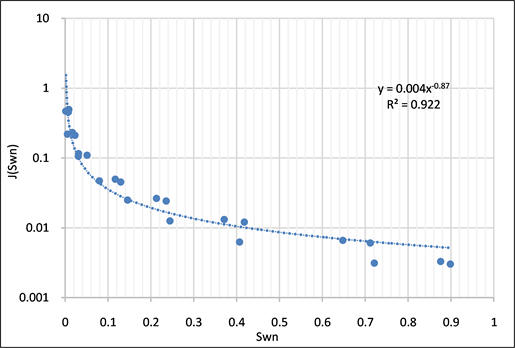
Figure 2. J function fitting of the seventh sample

图2. 第7类样品J函数拟合

Table 1. Reservoir classification criteria and 11 types of J functions

表1. 储层分类标准及11类J函数

将J函数代入式(式4) [8] ，得到实验室条件下11类平均毛管压力曲线 [12] 。

此次收集到的毛管压力所用实验方法为半渗透隔板法，实验介质为空气–盐水。半渗透隔板法与压汞法相比，实验系统更接近地下油藏实际情况，测试精度更高，数据更可靠。将得到的毛管压力曲线从实验室条件转换为地下油藏条件(式7) [11] ，σ和θ的取值参考了标准值以及邻区陆丰B油田的实验数据，取σ_labcosθ_lab为72，σ_rescosθ_res为28。得到11类平均毛管压力曲线(图3)。从第1类到第11类毛管压力曲线的启动压力、饱和度中值压力逐渐增高，平缓段变短，非润湿相饱和度增加。这说明随着I_rq减小，样品物性逐渐变差，孔喉半径逐渐减小。

据高压物性分析、地层水分析资料，取ρ_w = 1.02 g/cm³，ρ_o = 0.87 g/cm³，H为所在深度距自由水面的距离(m)，将得到的毛管压力曲线代入式3，计算得到任意高度的原始含水饱和度。

实际计算中，依据测井解释的孔隙度、渗透率对数据点进行分类，按照所属类别计算该数据点的J函数、毛管压力曲线，并最终得到原始含水饱和度。

图4为计算结果，从左到右，第一道为自然伽马曲线、钻头尺寸、井径尺寸；第二道为层位、第三道为中子、密度曲线、第四道为测井解释孔隙度、第五道为J函数计算含水饱和度及测井解释饱和度对比。蓝色曲线为印尼公式计算的含水饱和度，枚红色曲线为J函数计算原始含水饱和度。早期钻井(左侧) J含水计算饱和度与测井解释饱和度吻合较好，随着开发的进行，开发中晚期钻井(右侧)测井饱和度较原始含水饱和度明显增加，油水界面随之上升。

本次研究，基于J函数的含油饱和度建模结果见图5，主要过程如下：

1) 以相关反演结果为约束条件，采用续贯高斯方法模拟孔隙度分布。

2) 以孔隙度模型为约束条件，采用续贯高斯方法模拟渗透率分布。

3) 在孔隙度、渗透率模型的基础上，根据上述11类储层分类标准，计算储层分类模型。

4) 结合流体界面深度认识及界面张力、润湿角等参数，分不同储层类型完成基于J函数的饱和度建模。

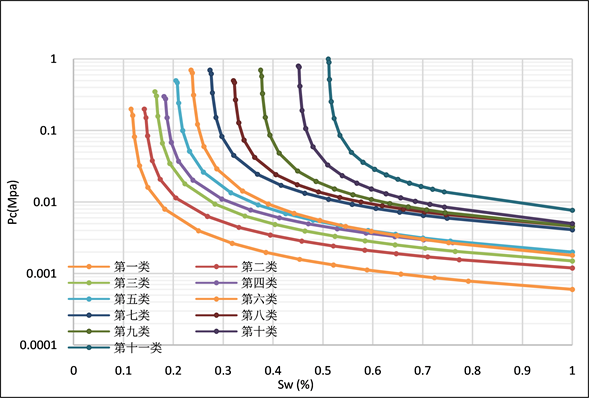
Figure 3. Mean capillary pressure curve

图3. 平均毛管压力曲线

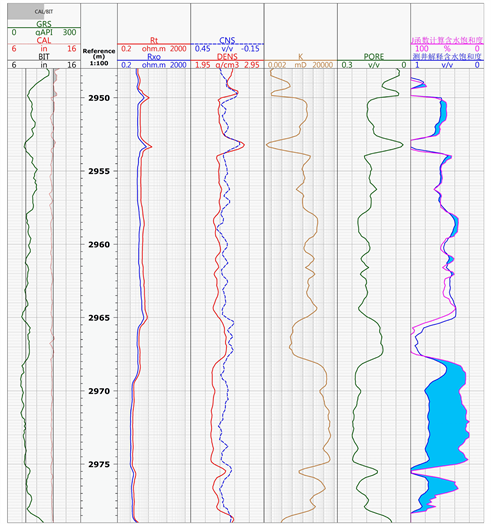
Figure 4. Water saturation comparison between calculation values using drilling J function and logging interpretation value

图4. 钻井J函数计算含水饱和度与测井解释含水饱和度对比

Figure 5. Geological model of main parameters in the Lufeng A block

图5. 陆丰A区块主要参数地质模型

从所建含水饱和度模型可以看出：在油水界面之上，高孔渗区对应高含油饱和度，与不同储层类型所对应的相渗端点值一致，体现了物性好的储层束缚水饱和度相对较低的规律；在油水界面上方，不同储层类型的具有不同的油水过渡带高度。上述模型特点更符合油藏实际情况，而传统饱和度插值方法是难以实现的。

4. 主要结论

1) 通过J函数计算原始含油饱和度的方法，计算的结果只与储层孔隙结构、油水密度、油柱高度有关，与电阻率无关，从而解决了水淹层测井解释含油饱和度不能代表原始含油饱和度的问题；利用储层质量系数分类的方法，充分考虑了储层的孔隙结构差异，准确地计算各类储层的原始水饱和度，在非均质性强的储层中得到了很好的运用。

2) 基于J函数方法建立的含油饱和度模型，与不同岩石类型相渗一致，能够体现不同岩石类型毛细管力所引起的流体过渡带，与传统插值方法所建立的含油饱和度模型相比，能够更加真实地反映油气藏原始含油饱和度分布。

基金项目

中海石油(中国)有限公司深圳分公司自立科研项目——南海东部在生产油田挖潜技术研究(YXKY-ZL-SZ-2016-04)。