双头铺放轨迹后处理技术研究

Research on Post-Processing Technique for Double-Heads Automated Placement

摘要: 为提升自动铺放装备工作效率并提高铺丝机工作的灵活度，对双机器人协同的类转体构件铺丝成型技术进行研究，提出了一个满足协调约束的轨迹预选机制。在确定了双机器人横向移动的配合方案后，以机器人平台可达空间的限制作为约束条件，通过夹角控制对铺丝轨迹进行配对编码并验证。同时得到完整模具的轨迹分配方案，将CAD软件生成的铺放信息转化成机器人角度的加工文件。文中模型证明所提方法满足大型类回转体构件铺放生产的工艺要求，大大提高了铺放效率。

Abstract: In order to improve the rate and kinematic dexterity of automated fiber placement system tech-nology, a dual-robot collaborative placement of similar rotation component is studied, and the method of primary trajectory that fits the constraints of coordination is put forward. After deter-mination of the matching scheme for the longitudinal feed of the robot, the AFP trajectory is paired by the Angle control, under the constraint of the robot platform’s full reachable workspace. At the same time, the track distribution scheme of the complete mould is obtained, and the information generated by CAD software is transformed into the machining document of robot Angle. This paper proves that the proposed method meets the process requirements of the production of large class gyro member, which greatly improves the laying efficiency.

1. 引言

多工位机器人协作系统已广泛应用在焊接领域，其具有设备成本较低、占用空间小，工作效率高，运动灵活的特点。伴随复合材料在航空航天领域的广泛应用，自动铺丝技术已成为高性能复合材料复杂构件的主流制造技术 [1] [2] [3] [4] ，使用机器人作为模块化铺放头的搭载平台的双头铺放系统可满足铺放大型复材构件，兼顾复材构件的复杂度与高生产率铺放。但是由于复合材料构件形状复杂，这对多工位铺丝机器人的铺丝轨迹分配、位姿协调控制提出了更高的要求。

相对于单个机器人系统而言，双机器人系统具有更高的灵活性和可靠性，能够完成更为复杂的任务 [5] [6] 。同时双机器人的协作任务也面临更为复杂的控制问题，如双机器人系统的路径规划问题 [7] [8] [9] ，机器人之间的避碰问题 [10] [11] [12] 等。近年来国内外研究人员已提出许多有效的控制策略 [13] ，主要包括动力学控制和运动学控制两种方法，其中运动学协调控制是目前较实用的方法。早期研究更多的是通过控制主机器人的位置而从机器人采用跟踪控制来协调其运动学约束关系的主/从控制方法 [14] 。后来，针对较复杂任务中同时需要兼顾力与位置的协调，提出了一种混合力与位置的控制方法，通过分别控制各机器人末端执行器的位置及外加力使其保持所需的运动约束关系 [15] 。本文从铺放机器人协调空间约束出发，以较复杂的类转体构件的铺放成型为研究对象，研究双机器人协调完成此类作业的运动规划问题，提出在时间和空间上两个机器人协调运作的轨迹分配方法。在CAD生成加工轨迹加工文件后，以双机器人系统的有效工作行程为动态约束进行轨迹再分配，降低后置处理难度。

2. 双头铺放系统行程范围计算

2.1. 坐标系的建立及包络方程的求解

模块化的铺丝头与机器人通过法兰盘连接(图1(a))，可以随时更换调试，能够更好地适应繁复的铺放环境。图1(b)中展示了由两台工业机器人组成的双工位铺放系统。

本文所采用的KR系列工业机器人结构示意，如图2所示，其后三关节轴线交于一点。判断模具是否可铺首先要计算机器人的工作能力，即末端执行器可达区域的最大范围曲面 [16] 。机器人工作空间正问题的求解方法一般有图解法、解析法和数值法三种。为了确定机器人工作空间旋转体的边界曲面和边界曲线，本文基于曲面包络和包络叠加的计算方法 [17] ，在解析法的基础上充分利用位姿解耦的特点，辅之以图示求解简化运动包络的解析计算。

(a) 位姿分离示意 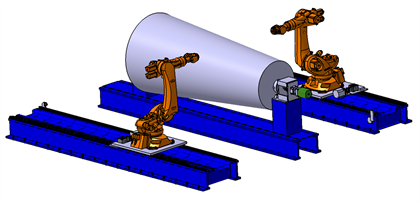(b) 拟采用机械结构

Figure 1. Structure schematic of dual-robot system

图1. 双机器人系统结构示意

图2. KUKA机器人D-H连杆机构图

将A4/A5/A6三轴交点(第三杆末端)记为P4org，其位置仅与机器人前三个关节转角相关，将点P4org的所有可达点的集合记为工作空间。

$G_{P_4}=\{\begin{array}{l}{x}_0=\left(a_2\pm \sqrt{a_3^2+d_4^2}\right)c_1{c}_2+a_1{c}_1\\ y_0=\left(a_2\pm \sqrt{a_3^2+d_4^2}\right)s_1{c}_2+a_1{s}_1\\ z_0=\left(a_2\pm \sqrt{a_3^2+d_4^2}\right)s_2\end{array}$ (1)

将式(1)整理后得到前三个关节的包络面方程(2)，

$x_0^2+y_0^2+z_0^2={\left(a_2\pm \sqrt{a_3^2+d_4^2}\right)}^2+a_1^2+2\left(a_2\pm \sqrt{a_3^2+d_4^2}\right)a_1{c}_2$ (2)

另外，将包络面根据θ1值的变化划分为若干层，使三维空间的包络面转化为二维空间的包络曲线进行分析 [18] 。当θ1 = 0时，三维机构退化为xoz的二维平面机构，可以进一步简化运算。由于模具在铺放过程中始终处于两个机器人的单侧位置，因此机器人不会出现背对模具的情况，可以舍去背部的包络空间。综上，得到机器人可达空间的一条包络曲线，如图3所示。该包络曲线的表达式可以将各连杆参数代入式(4)中得到。

$P_1{P}_2:{\left(x-350\right)}^2+{\left(y-675\right)}^2={\left(1150+\sqrt{{41}^2+{1000}^2}\right)}^2$

$P_2{P}_3:{\left(x-\left(350+1150\cdot \cos 5\right)\right)}^2+{\left(y-\left(675+1150\cdot \sin 5\right)\right)}^2={41}^2+{1000}^2$

$P_3{P}_4:{\left(x-350\right)}^2+{\left(y-675\right)}^2={472}^2$

2.2. 铺丝头的干涉约束

图1(a)中铺丝头姿态部分手腕长度为215 mm，自身长度685 mm，姿态部分总长为900 mm。将整个姿态部分近似为图4(a)中所示区域进行简化计算，为了避免与地面和底座的干涉，运动空间与地面距离需要设置500 mm的下限，还需要在机器人底座区域截取一个650 mm × 900 mm的矩形区域，如图4(b)所示，并将此区域带入到工作空间中，舍去重叠部分。

2.3. 双机器人系统主轴位置的确定

对图3的机器人包络空间分析可知，在距离底座1150 mm以上时，其包络线在水平方向上的投影最大，在实际工程应用中旋转主轴位置不宜过高。本文中将旋转主轴的高度设置为距离机器人底座1350 mm的高度上，在此高度上根据图解法估算将主轴的横向位置定位在距机器人底座中心约2700 mm的位置。两机器人的位置以主轴为中心对称分布。

Figure 3. A enveloping curve

图3. 一条包络曲线

3. 双头铺放轨迹分配策略

3.1. 两轨迹可铺放配对的判定

对于双头铺放系统而言，其铺放轨迹的分配是一个复杂的问题，主要涉及到双机器人有效工作行程的限制。根据铺放任务的特定需求，施压气缸对压辊提供压力使其与铺放模具表面接触，为了使压力完全均匀地作用于模具表面，一般情况下都是保证气缸的施压方向与机械臂末端坐标系的接近矢量同向。由于这一特殊的末端姿态约束条件，在工作时必须保证实时铺放轨迹点模具处延伸面同时位于两侧机器人腕点的可达包络空间内，图5所示。

具体计算步骤如下：

(1) 原始轨迹信息的参考坐标系为catia数模的坐标系，该坐标系与机器人基坐标系各轴指向可能不同。因此，在验证运算之前需要先对轨迹数据进行预处理，建立新的模具坐标系{B}(主轴坐标系)使得各轴指向与机器人基坐标系保持一致，坐标原点在模具回转轴线上。将包络模型转化到主轴坐标系下表示，简化位置关系的计算。设模具信息变换矩阵为 ${}_I^{B}T$ ，对于空间某点 ${\left(x,y,z\right)}^I$ ，该点在主轴坐标系下的坐标为：

${\left(x_r,y_r,z_r\right)}^B{=}_I^{B}T{\left(x,y,z\right)}^I$ (3)

(2) 对轨迹信息中的所有数据点沿法向外延900 mm即可获得铺丝腕点位置信息。从轨迹数据中提取法向信息单位向量Normal $\left(x_n,y_n,z_n\right)$ ，对于模具上某点 $\left(x_m,y_m,z_m\right)$ ，获得外延后的腕点信息 $\left(x_w,y_w,z_w\right)$ 为：

(a) 铺丝头区域 (b) 底座区域

Figure 4. Interference area schematic

图4. 干涉区域示意图

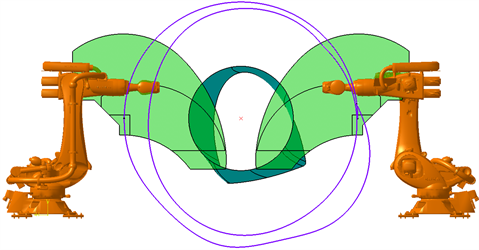
Figure 5. Automatic placing of work space for molds

图5. 模具铺放工作空间

$\{\begin{array}{c}{x}_w=x_m+900\times x_n\\ y_w=y_m+900\times y_n\\ z_w=z_m+900\times z_n\end{array}$ (4)

(3) 对每一条轨迹中的腕点数据沿轴向即z方向提取特征点。定义提取方法，一是为轨迹调度合法性提供判断依据，二是为初始解的生成服务。出于简化计算考虑，对于轨迹1，从边界点a1开始逐点判断下一个点沿z与a1的差值是否大于某一个设定的值，记为列宽 $\xi$ 。如果大于 $\xi$ ，将此点记为a2，如此类推，将所有的特征点都提取出来。

(4) 对于不同两条轨迹中的两个特征点T1i、T2i沿法向延伸处理得到控制ki、mi，将其绕主轴旋转分别与两侧包络曲线上下限相交得到ki'、mi'、ki''、mi''。如图6所示，O点为模具主轴中心点。

由于主轴作为冗余轴的存在，从理论上来说，如果两条轨迹中的对应的控制点过O点夹角能够在(α，β)区间内，便可通过对主轴的处理使得两个特征点都能处于机器人可达空间内。对两条配对的轨迹按点号逐点验证，直到所有点搜索完毕，以此作为轨迹配对的筛选准则。

3.2. 轨迹配对的优选

在获得构件所有铺放轨迹后，如果能够将它们相对均匀的分派给不同的铺放机器人上，则能提高整个任务的并行性，从而达到提高铺放效率的目标。定义一个主机器人(master robot，MR)，事先为其选择轨迹i，根据轨迹分配原则寻找从机器人(slave robot，SR)配对轨迹j。由于类转体构件的近似对称性，不妨设轨迹j的编号为pi，则

$p_i=\pm k+W,1\le i\le m,$ (5)

其中，m为构件铺放任务轨迹的总数，W为常数，这里令 $W=m/2$ 。k为叠加算子，取(0，W)之间的整数，其符号交替变换。如果在定义的分配原则条件下，找不到第i条轨迹配对的轨迹，此时主机器人单独执行第i条轨迹。

4. 实例验证

针对曲率变化较大的模型如图7所示，采用本文所述的算法进行轨迹配对及优化。通过两种方式进行验证：

基于三角面片的固定角轨迹规划算法，以模具主轴为参考轴获得45˚铺放角所有轨迹信息后，以其中一条为引导，寻找出能够适应分配算法的所有轨迹，并取出若干具有明显特征的轨迹进行对比。

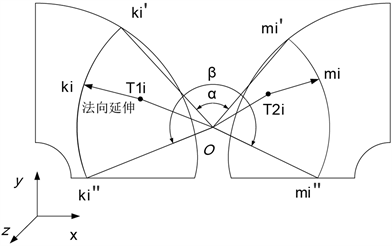
Figure 6. The schematic diagram of Angle interval determines

图6. 夹角区间判定示意图

该模型完整轨迹共有51条，如图7所示，以第1条轨迹为引导，分别将第15条轨迹和第25条轨迹的数据代入算法中。可以看到第25条轨迹(图8(b))可以完成与引导轨迹的配合，而第15条轨迹(图8(a))则始终处于验证夹角的下限(即α)附近，不能达到协同铺放的要求。

在前一步工作的基础上，寻找出完整模具的轨迹分配方案。通过高层控制模块完成任务分配和突发情况下的机器人的任务再规划。并且将基于模具角度的轨迹信息整合梳理转化成机器人中间变量，即从机器人的角度来表达轨迹分配结果，表1所示。

5. 结论

通过针对类回转体构件的分析，在完成两个机器人平台的轴向进给速率的配合后，运用本文提出的方案可以在铺放后置处理前有效地完成轨迹再规划。以机器人包络空间为限制，通过夹角控制进行轨迹预分配，将双工位平台的铺放协作问题简化成两个单工位平台的铺放后处理问题，降低计算难度同时可

图7. 验证模具及特征轨迹

(a) (b)

Figure 8. Partial trajectory verification results

图8. 部分轨迹的验证结果

Table 1. Complete trajectory allocation plan

表1. 完整轨迹分配方案

提高铺放效率。该策略形成了一般性类转体模具轨迹分配的一般步骤，对于保证双机器人与旋转主轴协作任务的完成具有重要意义。

基金项目

“高档数控机床与基础制造装备”科技重大专项：2016ZX04002-001-07。