一种用于双组份爆轰的格子Boltzmann模型

A Lattice Boltzmann Model for Binary Components Detonation

摘要: 本文提出了一种用于描述双组份爆轰现象的格子Boltzmann模型。为了模拟爆轰过程中的流动，我们使用双平衡态分布函数分别描述反应物和产物的密度、动量、能量；采用Lee-Tarver反应率函数描述化学反应。该模型能够实现化学反应和流动的自然耦合。数值结果表明，本文所提出的模型可以用来模拟爆轰现象。

Abstract: In this paper, we present a lattice Boltzmann model for simulating the binary components detonation phenomena. For modeling the flow behavior in the detonation process, we employ two distribution functions for the density, momentum and energy of reactant and product, respectively. The Lee-Tarver model is selected to describe the chemical reaction kinetics. The reaction heat is naturally coupled with the flow behavior. The numerical examples show that the scheme can be used to simulate the detonation phenomena.

1. 引言

爆轰现象是伴有能量释放的化学反应动力学过程。爆轰过程释放的巨大能量曾造成了很多毁灭性的灾难，因此人们最初研究爆轰主要是在安全防护、防爆和熄爆等领域。随着对爆轰形成和传播机理的了解，人们开始对爆轰加以利用，特别是随着航空航天和国防事业的发展，爆轰已经成为研究的热点之一。

近年来，爆轰现象的数值模拟虽然得到了快速发展，但其物理建模仍面临两大挑战：一是如何描述爆轰波阵面，传统的方法虽然能够处理间断面，但不能忠实地描述波阵面。二是如何描述流场中的化学反应和能量释放的过程，主要依赖于更加合理的化学反应模型。在文献资料中常见的爆轰问题数值模拟方法有欧拉法 [1] [2] [3] 、ALE法 [4] [5] 、level set方法 [6] [7] 、VOF法 [8] 、阵面追踪法 [9] [10] 等。近年来，随着高速可压缩流体的格子Boltzmann建模和模拟的发展，格子Boltzmann方法也被用于模拟爆轰现象 [11] - [17] 。

本文提出了用于描述双组份爆轰现象的格子Boltzmann模型，为了模拟爆轰过程中的流动，我们使用双平衡态分布函数分别描述反应物和产物的密度、动量、能量；在连续极限下，该模型可以恢复Navier-Stokes方程。化学反应采用目前应用最为广泛的反应率模型之一Lee-Tarver反应率函数 [18] 描述。化学反应放能过程和流动过程相耦合，内能的增加引起压强的变化，进而影响流体的宏观流动。数值结果表明，本文所提出的模型可以用来模拟爆轰现象。

2. 格子Boltzmann模型

2.1. 描述流动的双组份格子Boltzmann模型

离散速度模型采用Watari和Tsutahara [19] 提出的D2V33模型，该模型具有33个离散速度， $v_0=0$ ， $v_{ki}=v_k\left[cos\left(i\text{π}/4\right),sin\left(i\text{π}/4\right)\right]$ ，下标 $k=1,2,3,4$ 代表第 $k$ 组粒子速度是 $v_k$ ； $i=1,\cdots ,8$ 表示粒子速度方向。在本文的数值模拟中， $v_1=1.00$ 、 $v_2=1.92$ 、 $v_3=2.99$ 、 $v_4=4.49$ 。该离散速度模型能够满足恢复Navier-Stokes方程所需的七阶各向同性。

分布函数 $f_{ki}^{\sigma }$ 遵循以下格子Boltzmann方程：

$\frac{\partial f_{ki}^{\sigma }}{\partial t}+v_{ki}\cdot \frac{\partial f_{ki}^{\sigma }}{\partial r}=-\frac{1}{{\tau }^{\sigma }}\left[f_{ki}^{\sigma }-f_{ki}^{\sigma ,eq}\right]$ . (1)

其中， $\sigma \in \left(r,p\right)$ ，分别表示反应物和产物； $r$ 和 ${\tau }^{\sigma }$ 分别表示空间坐标和 $\sigma$ 组份的松弛因子， $f_{ki}^{\sigma ,eq}$ 为 $\sigma$ 组份的局域平衡态分布函数。

定义 $\sigma$ 组份的粒子质量为 $m^{\sigma }$ ，则 $\sigma$ 组份的局部密度为

${\rho }^{\sigma }=m^{\sigma }{\displaystyle \underset{ki}{\sum }{f}_{ki}^{\sigma }}$ . (2)

定义 $\sigma$ 组份的局部动力学速度为

$n^{\sigma }{u}^{\sigma }={\displaystyle \underset{ki}{\sum }{f}_{ki}^{\sigma }{v}_{ki}}$ , (3)

其中 $n^{\sigma }$ 为粒子数密度。局域平均密度为

$u=\frac{{\rho }^r{u}^r+{\rho }^p{u}^p}{{\rho }^r+{\rho }^p}$ . (4)

定义 $\sigma$ 组份的温度为

${\rho }^{\sigma }{T}^{\sigma }=P^{\sigma }=e_{therm}^{\sigma }=m^{\sigma }{\displaystyle \underset{ki}{\sum }\frac{1}{2}{v}_{vi}^2{f}_{ki}^{\sigma }-}\frac{1}{2}{\rho }^2{\left(u^{\sigma }\right)}^2$ , (5)

其中 $e_{therm}^{\sigma }$ 和 $P^{\sigma }$ 为 $\sigma$ 组份的内能和压力。局域平均温度

$T=\frac{{\rho }^r{T}^r+{\rho }^p{T}^p}{{\rho }^r+{\rho }^p}$ . (6)

$\sigma$ 组份的局域平衡态分布函数 $f_{ki}^{\sigma ,eq}$ 由下式给出

$\begin{array}{c}{f}_{ki}^{\sigma ,eq}=n^{\sigma }{F}_k\{\left[1-\frac{u^2}{2{\theta }^{\sigma }}+\frac{u^4}{8{\left({\theta }^{\sigma }\right)}^2}\right]+\frac{v_{ki\epsilon }{u}_{\epsilon }}{{\theta }^{\sigma }}\left(1-\frac{u^2}{2{\theta }^{\sigma }}\right)+\frac{v_{ki\epsilon }{v}_{ki\pi }{u}_{\epsilon }{u}_{\pi }}{2{\left({\theta }^{\sigma }\right)}^2}\left(1-\frac{u^2}{2{\theta }^{\sigma }}\right)\\ +\frac{v_{ki\epsilon }{v}_{ki\pi }{v}_{ki\upsilon }{u}_{\epsilon }{u}_{\pi }{u}_{\upsilon }}{6{\left({\theta }^{\sigma }\right)}^3}+\frac{v_{ki\epsilon }{v}_{ki\pi }{v}_{ki\upsilon }{v}_{ki\xi }{u}_{\epsilon }{u}_{\pi }{u}_{\upsilon }{u}_{\xi }}{24{\left({\theta }^{\sigma }\right)}^4}\}\end{array}$ , (7)

其中， ${\theta }^{\sigma }=T/m^{\sigma }$ ，权重因子 $F_k$ 和 $F_0$ 与文献 [15] [20] 一致。

式(2)、(3)和(5)分别为密度、动量和能量的定义，其分布函数 $f_{ki}^{\sigma }$ 可用局域平衡态分布函数 $f_{ki}^{\sigma ,eq}$ 替代。此外，局域平衡态分布函数 $f_{ki}^{\sigma ,eq}$ 还需满足以下矩关系

$m^{\sigma }{\displaystyle \underset{ki}{\sum }{v}_{ki\alpha }{v}_{ki\beta }{f}_{ki}^{\sigma ,eq}}=e_{therm}^{\sigma }{\delta }_{\alpha \beta }+{\rho }^{\sigma }{u}_{\alpha }^{\sigma }{u}_{\beta }^{\sigma }$ , (8)

$m^{\sigma }{\displaystyle \underset{ki}{\sum }{v}_{ki\alpha }{v}_{ki\beta }{v}_{ki\gamma }{f}_{ki}^{\sigma ,eq}}=e_{therm}^{\sigma }\left(u_{\gamma }^{\sigma }{\delta }_{\alpha \beta }+u_{\alpha }^{\sigma }{\delta }_{\beta \gamma }+u_{\beta }^{\sigma }{\delta }_{\gamma \alpha }\right)+{\rho }^{\sigma }{u}_{\alpha }^{\sigma }{u}_{\beta }^{\sigma }{u}_{\gamma }^{\sigma }$ , (9)

$m^{\sigma }{\displaystyle \underset{ki}{\sum }\frac{1}{2}{v}_k^2{v}_{ki\alpha }{f}_{ki}^{\sigma ,eq}}=2e_{therm}^{\sigma }{u}_{\alpha }^{\sigma }+\frac{1}{2}{\rho }^{\sigma }{\left(u^{\sigma }\right)}^2{u}_{\alpha }^{\sigma }$ , (10)

$m^{\sigma }{\displaystyle \underset{ki}{\sum }\frac{1}{2}{v}_k^2{v}_{ki\alpha }{v}_{ki\beta }{f}_{ki}^{\sigma ,eq}}=\left[2\frac{T^{\sigma }}{m^{\sigma }}+\frac{1}{2}{\left(u^{\sigma }\right)}^2\right]e_{therm}^{\sigma }{\delta }_{\alpha \beta }+\left[3e_{therm}^{\sigma }+\frac{1}{2}{\rho }^{\sigma }{\left(u^{\sigma }\right)}^2\right]u_{\alpha }^{\sigma }{u}_{\beta }^{\sigma }$ , (11)

反应物和产物的密度、速度和压力分别从(2)、(3)和(5)式中求出。当反应物和产物处于局域平衡态时，通过(6)式计算反应物和产物的 $f_{ki}^{\sigma ,eq}$ ，并在求解过程中使用相同的 $u$ 和 $T$ 。两个组份的分布函数不是相互独立的，而是通过碰撞项互相耦合。两个格子Boltzmann方程的耦合是通过在求解 $f_{ki}^{\sigma ,eq}$ 过程中引入相同的 $u$ 和 $T$ 实现的。

将方程(1)的左端用Lax-Wendroff有限差分格式离散，右端添加色散项和附加粘性项，并用二阶中心差分格式离散，得到以下形式的有限差分格子Boltzmann方程 [20]

$\begin{array}{c}{f}_{kiI}^{\sigma ,new}=f_{kiI}^{\sigma }-\frac{c_{ki\alpha }}{2}\left(f_{kiI+1}^{\sigma }-f_{kiI-1}^{\sigma }\right)-\frac{\Delta t}{\tau }\left(f_{kiI}^{\sigma }-f_{kiI}^{\sigma ,eq}\right)+\frac{c_{ki\alpha }^2}{2}\left(f_{kiI+1}^{\sigma }-2f_{kiI}^{\sigma }+f_{kiI-1}^{\sigma }\right)\\ +\frac{c_{ki\alpha }\left(1-c_{ki\alpha }^2\right)}{12}\left(f_{kiI+2}^{\sigma }-2f_{kiI+1}^{\sigma }+2f_{kiI-1}^{\sigma }-f_{kiI-2}^{\sigma }\right)+\frac{{\theta }_{\alpha I}^{\sigma }\left|k_{\alpha }^{\sigma }\right|\left(1-\left|k_{\alpha }^{\sigma }\right|\right)}{2}\left(f_{kiI+1}^{\sigma }-2f_{kiI}^{\sigma }+f_{kiI-1}^{\sigma }\right).\end{array}$ (12)

其中， $c_{ki\alpha }=v_{ki\alpha }\Delta t/\Delta r_{\alpha }$ ， $k_{\alpha }^{\sigma }=u_{\alpha }^{\sigma }\Delta t/\Delta r_{\alpha }$ ， ${\theta }_{\alpha I}^{\sigma }={\eta }^{\sigma }\left|\frac{P_{\alpha I+1}^{\sigma }-2P_{\alpha I}^{\sigma }+P_{\alpha I-1}^{\sigma }}{P_{\alpha I+1}^{\sigma }+2P_{\alpha I}^{\sigma }+P_{\alpha I-1}^{\sigma }}\right|$ ， $I-2$ 、 $I-1$ 、 $I$ 、 $I+1$ 、 $I+2$

代表 $x$ 或 $y$ 方向的5个连续点。修正的Lax-Wendroff格式是单调的守恒格式，能够改善数值稳定性。方程(12)的最后一项为附加粘性项，使模型既适用于低速不可压流体，又适用于高Mach系统，使稳定冲击与爆轰问题的模拟成为可能。

2.2. Lee-Tarver反应率函数

爆轰中的化学反应过程是十分复杂的，严格的化学反应动力学研究十分困难。在爆轰的数值模拟中，必须给出化学反应率。选用合适的化学反应率至关重要，因为它决定着计算出来的燃烧和爆轰的点火、发展和传播过程。目前对化学反应过程的模拟还处在使用唯象模型的阶段，Lee-Tarver反应率函数 [18] 是使用最广泛的化学反应模型之一。作为初步研究，本文的Lee-Tarver反应率函数和初始条件可以写成如下形式：

$\frac{\text{d}\lambda }{\text{d}t}=\{\begin{array}{l}a\left(1-\lambda \right)+b\left(1-\lambda \right)\lambda ,T\ge T_{th},且0\le \lambda \le 1\\ 0,其它\end{array}$ (13)

其中， $a$ 、 $b$ 为常数， $T_{th}$ 为化学反应的温度阈值。

爆轰化学反应的时间尺度比宏观流动的时间尺度小几个数量级，化学反应区内反应物的性质及化学反应细节极其复杂，使得化学反应流动方程组难以线性化和解耦处理，即化学反应和宏观流动不能用同一时间尺度描述。为此，我们采用算子分裂法求解方程(13)，化学反应的演化过程可以分为以下两步：

第1步，计算对流的贡献

$\frac{\partial \lambda }{\partial t}+u\nabla \lambda =0$ ,(14)

可由迎风格式求出

$\frac{{\lambda }_I^{n+1}-{\lambda }_I^n}{\Delta t}=-\{\begin{array}{l}\frac{u\left({\lambda }_I^n-{\lambda }_{I-1}^n\right)}{\Delta x},u\ge 0\\ \frac{u\left({\lambda }_{I+1}^n-{\lambda }_I^n\right)}{\Delta x},u<0\end{array}$ ,(15)

其中， $I-1$ 、 $I$ 、 $I+1$ 代表 $x$ 或 $y$ 方向的3个连续点。

第2步，计算化学反应的贡献

$\frac{\partial \lambda }{\partial t}=a\left(1-\lambda \right)+b\left(1-\lambda \right)\lambda$ , (16)

其解析解为

${\lambda }_I^{n+1}=\frac{{\text{e}}^{\left(a+b\right)\Delta t}+a\left({\lambda }_I^n-1\right)/\left(a+b{\lambda }_I^n\right)}{{\text{e}}^{\left(a+b\right)\Delta t}+b\left(1-{\lambda }_I^n\right)/\left(a+b{\lambda }_I^n\right)}$ .(17)

2.3. 化学反应与流动的耦合

在真实的燃烧过程中，化学反应放出的热量和内能是耦合的。化学反应放出热量必然导致内能增加，内能的增加引起压强的变化，进而影响密度和流速的变化。相应地，在我们所构建的格子Boltzmann模型中，总的内能的变化率 $\stackrel{\dot{}}{e}$ 包含两部分：化学反应部分 ${\stackrel{\dot{}}{e}}_{chem}$ 和原来的热力学部分 ${\stackrel{\dot{}}{e}}_{therm}$ 即

$\stackrel{\dot{}}{e}={\stackrel{\dot{}}{e}}_{therm}+{\stackrel{\dot{}}{e}}_{chem}$ , (18)

${\stackrel{\dot{}}{e}}_{chem}=\stackrel{\dot{}}{\lambda }\rho Q$ .(19)

其中， $Q$ 表示单位质量反应物发生化学反应放出的热量，即爆热；局域平局密度 $\rho ={\rho }^r+{\rho }^p$ 。

在格子Boltzmann模拟过程中，首先从方程(5)中得到热力学部分的内能 $e_{therm}$ ，然后通过式(18)-(19)计算总的内能 $e$ ；再用总内能 $e$ 替代 $e_{therm}$ 并更新压力 $P$ 和温度 $T$ ；最后通过下式更新反应物和产物的密度

${\rho }^{r,new}={\rho }^r-\stackrel{\dot{}}{\lambda }\rho$ ,(20)

${\rho }^{p,new}={\rho }^p+\stackrel{\dot{}}{\lambda }\rho$ . (21)

通过这样的过程，化学反应能和流场实现了自然耦合。

3. 数值例子

3.1. 带有黏性和热传导的活塞问题

考虑一均匀充满可燃气体的爆轰管，爆轰管左端为一稳定爆轰波，初始条件为：

${\left(\rho ,u,v,T,\lambda \right)}_L=\left(1.35,0.81,0,2.65,1\right)$ , (22)

${\left(\rho ,u,v,T,\lambda \right)}_R=\left(1,0,0,1,0\right)$ . (23)

上边界和下边界为循环边界条件，左边界为固壁边界条件，右边界为流出边界条件。其它参数为：空间步长 $\Delta x=\Delta y=0.001$ 、时间步长 $\Delta t={10}^{-5}$ 、爆热 $Q=1.0$ 、绝热指数 $\gamma =2.0$ 、化学反应温度阈值 $T_{th}=1.10$ 、网格数 $N_x\times N_y=1000\times 3$ ；Lee-Tarver反应率函数中的参数为 $a=1$ 、 $b={10}^3$ 。

图1(a)~(d)给出了活塞速度 $u_p=0.81$ 时，不同时刻的宏观物理量密度 $\rho$ 、压力 $P$ 、流速 $u$ 和温度 $T$ 。

Figure 1. Physical quantity profiles for the piston problem including effects of viscosity and heat conduction at times 0, 0.05, 0.1, 0.15, 0.2, 0.25 and 0.3: (a) density $\rho$ ; (b) pressure $P$ ; (c) x-component of velocity $u$ ; (d) temperature $T$

图1. 在0，0.05，0.1，0.15，0.2，0.25时刻的带有黏性和热传导的活塞问题的宏观物理量曲线：(a) 密度 $\rho$ ；(b) 压力 $P$ ；(c) x方向的速度分量 $u$ ；(d) 温度 $T$

图中可以清晰地观测到爆轰波的von Neumann峰、化学反应区和Taylor稀疏波等基本特征。此时活塞流速等于CJ爆轰的流速，爆轰波阵面与活塞之间有一个均匀态即CJ态，由于流动是以声速进行的，在活塞处生成的稀疏波不能赶上爆轰波阵面。

爆轰波的Hugoniot关系为

${\rho }_0\left(D-u_0\right)={\rho }_1\left(D-u_1\right)$ , (24)

$P_1-P_0={\rho }_0\left(D-u_0\right)\left(u_1-u_0\right)$ , (25)

$e_1-e_0=0.5\left(P_1+P_0\right)\left(1/{\rho }_0-1/{\rho }_1\right)+\lambda Q$ , (26)

下标0和1分别表示爆轰波阵面前、后的物理量，D为爆轰波速度。为验证爆轰波的Hugoniot关系，我们测得此时爆轰波的速度 $D=3.1$ ，通过格子Boltzmann模型求得爆轰波后的宏观物理量为 $\left(\rho ,u,P)=(1.35,0.82,3.54\right)$ ，带入(24)~(26)式，方程左端的计算结果为3.09，2.54，1.64，方程右端的计算结果分别为3.08，2.52，1.58，与左端值相比，三个方程右端对左端的偏差分别为3%，8%，4%。由于在爆轰波的Hugoniot中，忽略了黏性和热传导的影响，所以格子Boltzmann的模拟结果是令人满意的。数值结果充分表明，本文所提出的格子Boltzmann模型符合爆轰波的Hugoniot关系，可以用于爆轰的冲击起爆问题。

3.2. 爆轰波的正规反射和Mach反射

考虑一矩形计算域内均匀充满可燃气体，如图2所示。(a)~(d)不同颜色曲线分别表示从起爆至产生Mach反射过程中四个阶段的爆轰波。在相距为 2L 的A、B两点同时起爆，产生两个相同的柱面散心爆轰波a；这两列爆轰波传播到对称面处发生对撞形成b；接着继续向前传播产生正规反射波c；之后进一步向前传播产生Mach反射波d。由于在相互作用点处压强相对较高，所以在对称面附近会引起速度的增加，初始的Mach反射波会逐渐追赶上散心入射波，最后两爆轰波阵面趋于一致。计算域的初值条件为：

$\left(\rho ,u,v,T,\lambda \right)=\left(1.36,0.82,0,2.60,1\right)$ ，在A点和B点处，

$\left(\rho ,u,v,T,\lambda \right)=\left(1,0,0,1,0\right)$ ，其他位置.

网格数 $N_x\times N_y=1000\times 3$ ，其他参数与图1相同。

图3(a)~(d)给出了爆轰波正规反射和Mach反射的演化过程。由于两爆轰波关于对称面对称，为简单起见，我们只给出了下半个计算域内不同时刻流场的压强分布。图3(a)为爆轰波的起爆，并产生爆轰波的过程；图3(b)为爆轰波的正规反射；当入射角大于极限角时，正规反射开始向Mach反射转变，如图3(c)所示。此时，计算得到极限角的解析值 [21] 为 ${\alpha }_c={27.67}^{\circ }$ ，通过本文模型所得到的极限角为 ${{\alpha }^{\prime }}_c={26.45}^{\circ }$ ，

Figure 2. Sketch of regular and Mach reflections of detonation wave

图2. 爆轰波的正规反射和Mach反射模型示意图

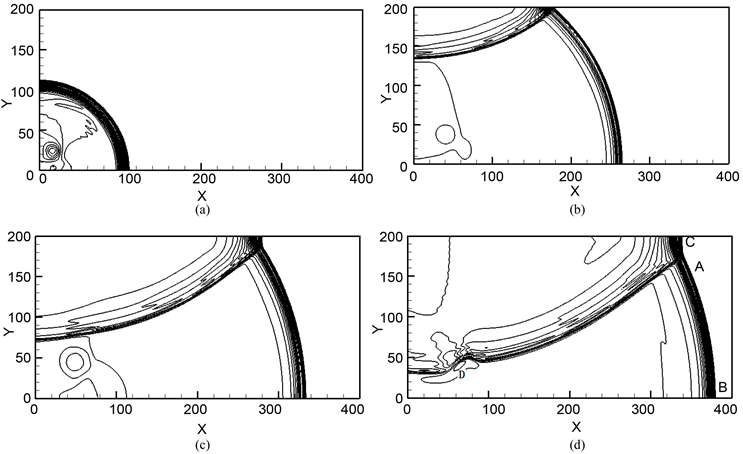
Figure 3. The transition process from regular reflection to Mach reflection: (a) Ignition arises and detonation waves generate; (b) The regular reflection of detonation wave; (c) Conversion from the regular reflection to Mach reflection; (d) The Mach reflection of detonation wave

图3. 爆轰波正规反射和Mach反射的演化过程：(a) 起爆产生爆轰波；(b) 爆轰波的正规反射；(c) 爆轰波正规反射向Mach反射转变；(d) 爆轰波的Mach反射

与解析值相比，本文模拟结果与解析值的相对误差约为4.1%。由于格子Boltzmann模型包含了粘性和热传导的影响，其结果是令人满意的；图3(d)为爆轰波的Mach反射。在爆轰波相互作用点附近形成三波点A，其中AB为入射的爆轰波，AC为Mach杆，AD为反射的冲击波，与文献 [22] 所得结果相吻合。

4. 结论

本文提出了用于双组份爆轰的格子Boltzmann模型。流场采用两个平衡态分布函数分别描述反应物和产物的密度、动量和能量。使用Lax-Wendroff有限差分格式和二阶中心差分格式将格子Boltzmann方程离散，使模型既适用于低速不可压流体，又适用于高Mach系统。化学反应采用Lee-Tarver反应率函数描述，实现了化学反应和流体流动的自然耦合。通过对带有粘性和热传导的活塞问题以及爆轰波正规反射与Mach反射问题的计算，数值结果表明，本文所提出的模型能够用于爆轰问题的数值模拟。

基金项目

国家自然科学基金(NO. 51406067, NO. 11272133)，吉林省教育厅科研项目(吉教科合字[2016]第141号)资助。