基于小波分析的高原山地区径流变异性分析

Analysis of the Radial Rheological Characteristics of Plateau Mountain Area Based on Wavelet Analysis

摘要: 水文周期预报是水资源管理的重要内容，针对西南高原山地区域径流变化差异大特点，本文以云贵高原洒渔河流域为例，根据上中下四个站点1954~2013年径流资料，采用小波分析法对径流变化特征进行研究。研究表明：区域径流第一主周期表现为一致性(四个站点第一主周期均为18 a)，显示了大气环流是影响区域径流主周期变化的重要因素；区域径流的第二主周期变化存在明显的差异性(新街站和祖家坝闸站为28 a，而渔洞和黑石罗为11 a)，显示了高原山地对径流波动的重要作用；因此采用第一主周期叠加第二主周期长短结合的方法，对于高原山地径流水文周期预报具有较好的作用和意义。

Abstract: Hydrological cycle forecast is an important part of water resources management. For the characteristics of runoff variation in the mountainous area of the southwest plateau, this paper takes the sprinkler river basin in the Yunnan-Guizhou Plateau as an example. According to the runoff data on the four sites in 1954~2013, this paper studies the characteristics of runoff variation. The results show that: the regional runoff first cycle shows consistency (the first main period of the four sites is 18 a), indicating that the atmospheric circulation is an important factor affecting the main cycle variation of the regional runoff; the second period of change of regional runoff has obvious differences (the period of Xinjie station and Zujiabazha station is 28 a; that of Yudong station and Heishiluo station is 11 a), showing the important effect of plateau mountain on runoff fluctuation. Therefore, the method combining the first main cycle and the second main cycle is used, which has a good effect and significance for hydrological cycle forecast of the plateau runoff.

1. 引言

水文周期预报是水资源管理的重要内容，因此作出准确的预报尤为重要，为了提高水文周期水文预报的精度，确保水文周期预报的可靠性，人们应用不同的学科知识相结合从各个方向来研究，为水文周期预报提出了很多方法。这些方法一般分为传统方法和新方法，前者主要根据河川径流的变化具有连续性、周期性、地区性和随机性等特点而发展的成因分析和水文统计方法，后者是由于计算机技术和数学的不断发展而产生的，包括小波分析、模糊数学、人工神经网络、灰色系统分析、混沌理论等以及这些方法的相互耦合，每种方法都开展了大量研究。小波变换具有时频局部化特征，能够揭示水文序列变化的多时间尺度结构，周期变化的局部化特征及周期随时间的变化情况，利用小波变换分析水文径流时间序列的多尺度特征，可以为流域径流水文周期预报及水资源合理配置提供重要依据。

近年来小波分析发展十分迅速，成为了国际研究热点，也在众多的现代动态测量领域都取得相当可观的成果，在数学方面研究金融、股市等发展；气象学方面研究地区气温、降水等变化情况；在计算机领域研究图像、故障等处理；在水利方面研究河川径流、泥沙等变化情况；给许多相关领域带来了崭新的思想，为其发展提供了有力的支撑。水文气象序列趋势变化特征是径流测报的基础性工作 [1] ，而Morlet小波是一种最常用的复数小波，它可以很好的把其趋势变化特征表现出来，因此它广泛的应用于国内外的水文气象趋势分析中。如王文圣等成功的将小波分析在水文时间序列趋势分析和多时间尺度分析中应用 [2] ；王秀杰等利用多分辨率小波函数，分别对黄河相关水文站实测日径流时间序列进行小波分析，分析结果显示小波分析的组合模型在径流预测数据抗干扰方面具有明显的优势 [3] ；周玉都等运用Morlet小波分析和Mann-Kendall法对廊坊市近50年9个气象站的气温数据，分析了廊坊市气温的时空变化特征 [4] ；万星等将小波变换与BP神经网络相结合应用于黄河陕县水文站长时间水文径流序列，得到了径流序列的组成和变化情况 [5] ；邱海军等利用小波分析工具结合Hurst指数对洪涝灾害的1950~2010年的变化动态进行分析，定性的分析出了洪涝灾害的未来趋势变化情况 [6] ；刘晓琼等基于Morlet小波分析了渭河水沙长时间序列演变规律 [7] 。本文基于洒渔河相关测站实测径流资料，采用小波分析法，对洒鱼河径流的变化特征及其变化规律进行研究，揭示云南高原山地丘陵区域在高山峡谷的影响下流域径流周期演变规律，从而为流域水文周期预报和水资源科学管理提供决策依据。

2. 研究区概况

洒渔河为金沙江右岸支流，发源于滇东北鲁甸县境内的臭水井梁子架马石山，发源地海拔高程约为3110 m。河流自南向北流经龙树盆地，在闪桥以下进入峡谷，于跳石附近折向东南，流经渔洞水库后又折向东北进入洒渔坝子称洒渔河，并有右支流昭鲁大河、左支流冷水河加入，往下经箐口塘及小堡子站至高桥下游50 km与右岸的络绎河交汇，汇口以上洒渔河河长175 km，河道坡降12.6‰；汇口以下称大关河，在柿子纳入白水江经盐津后称为横江，最后在四川省宜宾市安边镇对岸注入金沙江，全长311 km，河道平均比降3.1‰，集水面积11,233 km²。

研究区属暖温带、半干旱高原季风气候，主要特点表现为雨季降水集中，枯季降水稀少，干湿季节明显，四季不分明。多年平均气温11.6℃，极端最高气温33.5℃，最低气温−13.3℃；多年平均降水量731 mm；蒸发量1679.6 mm；年平均相对湿度74.5%；定时最大风速24 m/s，相应风向SW；年日照时数1892.1h，日照率43%。区内径流深50~500 mm，其中昭鲁坝区50~150 mm，龙树坝区500 mm，小寨河谷200~300 mm；多年平均最大一日降水量50~75 mm。地表水资源量为7.686亿m³，地下水资源量为0.433亿m³，水资源总量为7.686亿m³。

本文资料来源云南水科院逐日径流资料，选取的站点为洒渔河上游新街，渔洞站点和支流冷水河黑石罗站，支流昭鲁大河祖家坝闸站。水系及站点如图1。

3. 研究方法

径流演变过程中包含多时间尺度变化特征，而复小波函数可以给出隐藏在径流时间序列中的周期变化情况，所以选择合适的复小波函数对于径流时间序列的揭示很重要。本文采用20世纪80年代初由Morlet提出的一种能从时、频两方面揭示水文径流时间序列的特征的复数小波，它能清晰的判断出水文径流时间序列的变化趋势和周期组成情况 [8] ，充分反映不同周期中的变化趋势，并通过对不同时间尺度下的小波系数按不同的方法处理，得出未来径流时间序列变化情况。

本文小波分析的关键就是对径流时间序列进行小波变换，实际上就是一簇小波函数来表示的时间函数f(t)，通过小波变换得到它的小波变换系数，而通过这些小波变换系数的研究可以用来显示它的隐含在径流时间序列中的时频域信息和其重要局部变化特征。因此设函数 $\psi \left(t\right)\in L^2\left(R\right)$ 表示在实数域 [9] ，对于满足许可条件的小波函数，其连续小波变换为

$W_f\left(a,b\right)={\left|a\right|}^{-1/2}{\displaystyle {\int }_{R}f\left(t\right)\bar{\psi }\left(\frac{t-b}{a}\right)}\text{d}t$ (1)

式中， $W_f\left(a,b\right)$ 为小波变换系数，它随a (尺度因子，反映小波的周期长度)、b (平移参数，反映时间上的平移)而变化，表示某一信号与对应点代表的小波函数的相似程度。 $\bar{\psi }\left[\left(x-b\right)/a\right]$ 为 $\psi \left[\left(x-b\right)/a\right]$ 的复共轭函数。

将小波系数的平方值在b域上积分，就可得到小波方差，即

$Var\left(a\right)={{\displaystyle {\int }_{-\infty }^{\infty }\left|W_f\left(a,b\right)\right|}}^2\text{d}b$ (2)

Morlet小波是一种最常用的复数小波，其尺度函数不存在，且不具有正交性，但其时、频两域具有很好的局域性，可以把径流演变规律很好的表现出来。本文基于上述Morlet小波分析高原山地立体气候下径流周期性变化规律。

4. 结果与分析

4.1. 洒渔河渔洞水库年际径流变化趋势

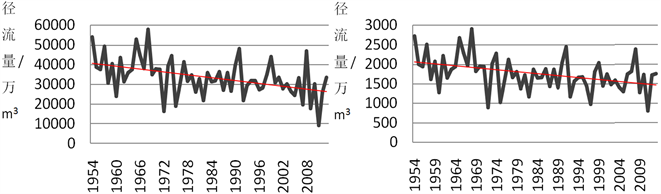
根据洒鱼河各站1954~2013年逐年实测径流资料来研究洒鱼河径流演变规律，绘制洒鱼河天然径流过程线及其

Figure 1. Water charts and sites

图1. 水系图及站点

趋势线(如图2)，以洒渔河上游渔洞站，新街站及支流黑石罗站，祖家坝闸站年径流序时间列为研究对象进行小波分析。

径流时间序列，也叫时间数列或动态数列，是某一要素按照时间顺序变动排列而形成的一种数列，它反映了随时间变化的要素的发展过程。径流时间序列的变化不是一种固定的周期运动，而是包含着不同的时间尺度(周期)的变化和局部波动变化，而通过Morlet复数小波可以将在径流时间序列中隐藏的时间尺度和局部突变点等特征表现出来。由图2可知，各站年径流量总体上均呈现下降趋势。

4.2. 小波分析

小波系数实部等值线图可反映流域年径流量的周期变换及强弱，小波系数实部为正时，代表丰水期，用实线表示；小波系数实部为负时，表示枯水期，用虚线表示；小波系数实部为0时，代表平水期，用粗实线表示。

图3为基于Matlab下的渔洞站、新街站、黑石罗站和祖家坝闸站的Morlet小波实部等值线图，从图中可看出四站的年径流呈现出不同时间尺度的周期变化情况。四站河川径流在尺度17~20 a尺度上震荡非常明显，存在丰–枯–丰–枯–丰的5个循环交替，其中1954~1957年，1965~1971年，1976~19811年，1987~1992年，1997~2004年，2010~2013年年径流偏丰；1958~1964年，1972~1975年，1982~1986年，1993~1996年，2005~2009年年径

(a) 渔洞站(Yudong) (b) 新街(Xinjie)(c) 祖家坝闸(Zujiabazha) (d) 黑石罗(Heishiluo)

Figure 2. The annual runoff time series and the trend of change

图2. 各站年径流时间序列及变化趋势图

(a) 渔洞站(Yudong) (b) 新街(Xinjie) (c) 祖家坝闸(Zujiabazha) (d) 黑石罗(Heishiluo)

Figure 3. Runoff wavelet coefficient real part contour map

图3. 径流小波系数实部等值线图

流偏枯；渔洞和黑石罗站在10~13 a时间尺度上震荡较为明显；新街和祖家坝闸站在25~30 a时间尺度上震荡较为明显。综上认为在研究区其波动周期以18 a为主，显示了大气环流是影响区域径流主周期变化的重要因素。

上述分析可知洒渔河上游及支流河川径流变化基本一致，都是以18 a左右尺度为第一主周期变化，各站在第一主周期变化存在相似性，能反映出洒渔河年径流量在时间域中的丰枯变化的特性和演变趋势；而在第二主周期上又存在一定的差异性，渔洞和黑石罗站第二主周期为11 a尺度，而新街和祖家坝闸站第二主周期为28 a尺度，在径流趋势没有太大变化的情况下反映了云南高原受地势地形影响相同区域河川径流演变过程存在差异，即高原山地立体气候对河川径流周期演变有一定的影响。

4.3. 小波检验

为进一步确定洒渔河年径流时间序列主周期，将计算的小波系数代入公式(2)即可得到小波方差，利用Matlab软件绘制小波方差图(图4)。

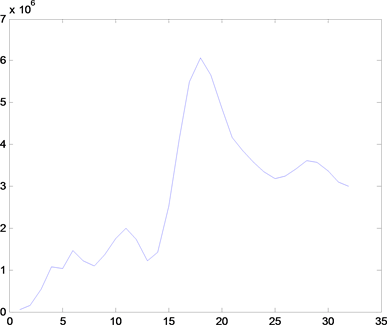(a) 渔洞站(Yudong) (b) 新街(Xinji e)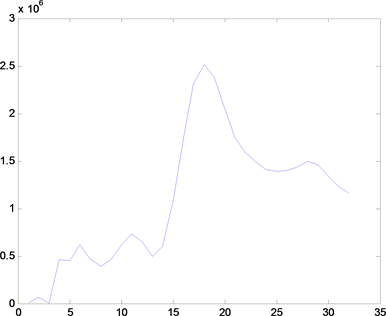(c) 祖家坝闸(Zujiabazha) 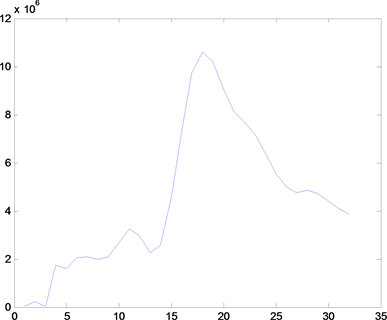(d) 黑石罗(Heishiluo)

Figure 4. Annual runoff wavelet variance

图4. 年径流量小波方差

小波方差反映了径流时间序列的信号波动能量随时间尺度的分布情况，可以通过小波方差图检验存在于径流时间序列的主要时间尺度 [10] [11] 。由图4可以看出，研究区径流在四个站的小波方差图存在很明显的峰值，可以确定小波方差反映的洒渔河流域径流变化的主周期依次为18 a、28 a、11 a，图中看出小波方差最大峰值对应着18 a的时间尺度，说明在18 a的时间尺度下周期震荡最强，所以洒鱼河流域第一主周期为18 a；而在第二主周期上四站存在明显差异，渔洞站和黑石罗站为11 a时间尺度，新街站和祖家坝闸站为28 a时间尺度。从小波方差峰值来看，控制着洒渔河流域变化特征的周期为18 a时间尺度；区域径流的第二主周期变化存在明显的差异性(新街站和祖家坝闸站为28 a，而渔洞和黑石罗为11 a)。因此在高原山地立体气候下的径流水文周期预报不能忽视第二主周期的影响，应考虑相关区域第二主周期的耦合，才能更精确的进行区域径流水文周期预报。

4.4. 径流变化特征分析

以上分析表明，洒渔河四站能量较强中心区，其尺度中心、震荡中心等在一定范围内基本一致。在18 a、28 a，11 a左右尺度的丰枯交替变化清晰，波动极值点分布规律明显，震荡行为明显。

为进一步分析其变化特征，选站点渔洞和新街绘制了小波系数(实部)过程线 [12] (见图5)。由图5可知，渔洞站径流量的丰枯期变化从11 a特征时间尺度上可以看出，大约经历了9个丰枯转换期；而在18 a时间尺度上，

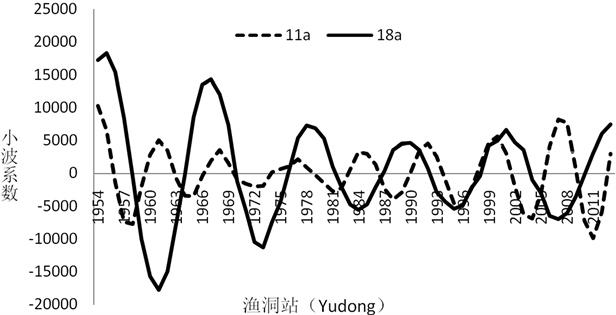
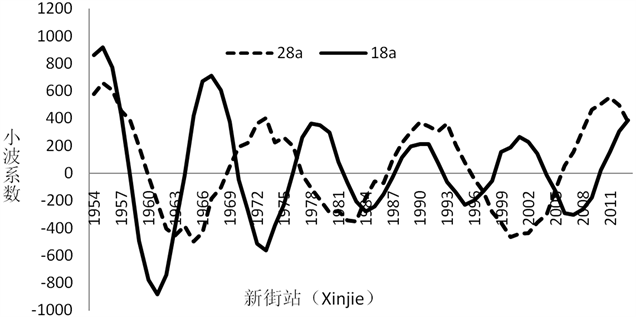
Figure 5. Wavelet coefficient (real part) process line

图5. 小波系数(实部)过程线

大约经历了5个丰枯转换期。新街站18 a左右时间尺度上基本一致，28 a时间尺度上，经历了2.5个丰枯变换周期。两站在18 a的时间尺度上，两者的变化趋势总体一致，渔洞和新街站径流的平均变化周期为12 a左右，干支流径流的丰枯变化也较为一致，可以作为径流水文周期预报的指导性周期，同时根据径流的丰枯周期，可以合理调整生产生活用水，保证城市生活供水情况。

在18 a主周期演变情况下，从曲线的波动趋势可以推断2013年以后的几年仍处于径流偏丰期，预计在2018年左右洒渔河流域将进入枯水期，持续时间7年左右。

通过与西南地区相关研究对比显示 [13] ：在全球气候变暖的影响下，其总体上径流变化与西南地区变化相一致，符合西南地区总体变化趋势(震荡周期范围及径流年际变化情况)，但区域上存在一定差异性；对比其他相关文献，一般小波分析文章只考虑第一主周期变化，从而确定水文变化情况，本文认为在特殊地区(存在高原山地气候影响区)水文预报应考虑第一主周期与第二主周期的耦合，对未来水文预报更具科学性。

5. 结论

1) 洒渔河径流1954~2013年多年平均径流深呈现减少趋势，流域径流存在明显的多时间尺度周期变化特征，其中渔洞和黑石罗依次为18 a、11 a、4 a，新街和祖家坝闸依次为18 a、28 a、11 a、6 a。

2) 洒渔河年径流周期变化总体上具有同步性，由于高山峡谷相间存在一定差异性，其表现在：从小波分析可以得出，洒渔河年径流具有18 a主周期变化规律，而在第二主周期上存在着差异。在18 a尺度主周期下，预计在2018~2024年以后洒渔河流域将处于枯水期。

3) 研究表明，西南高原山地特征的区域在小波变换分析中叠加第一主周期和第二主周期综合分析，既能体现大气环流主导影响，也能反映高原山地地形的波动影响，有助于提高径流水文周期的预报精度，同时对西南地区水资源水文周期管理具有重要意义。

基金项目

国家自然科学基金项目(51409274, 51679253)，云南省重大水利项目(YSZD-2014-001)，国家重点研发计划(2016YFC0401306)。