竖井壁面掺气坎布设位置的数值模拟研究

Numerical Simulation on the Position of the Aeration Step of a Shaft

摘要: 实验表明，采用竖井直段壁面掺气坎的方式对旋流竖井进行掺气保护是可行的。本文对不同位置壁面掺气坎进行数值模拟计算，并对比分析了各种情况下的水流流态、壁面压强和掺气空腔长度。结果表明：在不同位置布设壁面掺气坎对竖井内部水流流态和壁面压强影响不大；布设对称掺气坎时始终有一侧难以形成明显空腔，在进口来流方向近入口断面一侧壁面逆时针旋转90˚的位置布设一道掺气坎时，空腔长度最长并且全程均可形成稳定贯通的空腔。

Abstract: Experiments show that it is feasible to carry out aerosol protection on the vortex shaft by the way of the aeration step of the shaft. In this paper, numerical simulation is carried out on the different positions of the aeration step, and the flow regime, wall pressure and aeration cavity length in each case are analyzed and compared. The results show that there are few effects on the flow and wall pressure of the shaft in different locations. It is difficult to form a clear cavity on the side of the symmetrical aeration. At the inlet flow direction, when the clock is rotated by 90˚, the cavity is the longest and the whole can form a stable cavity.

1. 引言

旋流式竖井泄洪洞基本结构包括：进口段、上平段、涡室、收缩段、竖井直段、压坡段、下平段。竖井过流消能的原理为：水流自上平段沿切线进入涡室，受离心力作用而起旋，在涡室、收缩段、竖井段内，贴壁作螺旋运动，此后出射到流入消力井中，在水体与壁面的摩擦及水体在消力井内旋转、混掺、强剪切过程中，消去大部分能量 [1] [2] [3] [4] 。在大流量、高水头的情况下，愈靠近竖井段底部，水流铅直方向流速越大，贴壁效果越差，越容易发生空化空蚀现象，所以采用通气井或者掺气坎的方式对旋流竖井进行掺气保护一直是众多学者研究的重点。严维，王文 [5] 对两河口的竖井泄洪洞空化特性进行了研究；李瑶，张法星 [6] 等对旋流式竖井环形掺气坎的空腔进行了研究计算；吕利，邓军 [7] 等提出壁面全程掺气竖井，并建立了物理模型进行实验研究。对于壁面全程掺气竖井而言，由于水流自收缩段进入竖井直段发生突扩现象的过程中，大股集中水流极易冲击并淹没掺气坎而导致掺气效果不佳；故在竖井直段壁面选择何处布设纵向掺气坎是一个值得研究的问题。其研究意义在于：不仅对目前竖井直段壁面掺气坎的讨论拓展了一个新的研究方向，也为今后在实际工程中建造竖井直段壁面掺气坎时的位置选取具有一定参考价值。

2. 计算体型及网格划分

旋流竖井模型建立情况如图1，以水平向右为x轴正方向，竖直向上为y轴正方向，由内向外为z轴正方向；整个模型高174.5 m，进口尺寸为9 m × 7 m (宽 × 高)，入口底板高程为140 m，涡室顶部高程为154 m，涡室与收缩段连接处高程为111 m，收缩段与竖井段衔接处高程为90 m，涡室段直径为18 m，收缩段底部直径10 m。整个涡室长43 m，收缩段长21 m，竖井直段长90 m。竖井直段横剖尺寸如图2 (横剖面为竖直方向自下往上视角，后文皆如此)：两个半径为6.5 m的半圆相错衔接而形成两个对称分布的掺气坎，掺气坎位置首先布设于与入口来流方向一致的两侧，掺气坎宽1 m，沿竖井段往下铅直方向，每隔10 m设置两个对称分布的通气井，通气井宽度与掺气坎相同，水平方向延伸2 m，铅直方向加高1 m。

整个计算区域大部分采用结构化网格，尽量少的部分采用非结构化网格，由于主要针对竖井段内部水流的研究，故没有对反弧段和压坡段以后部分进行建模，并着重讨论竖井段内部水流的水力特性。考虑到水流紊动剧烈，但在竖井段基本能够贴壁流动，并着重讨论掺气空腔长度这一特性，所以整个竖井段均采用结构化网格，并将其环向壁面以及掺气坎空腔处网格进行了加密处理。整个控制体网格数约为54万，基本能够达到计算精度要求。

3. 模型算法与边界条件

本文采用质量守恒定律和动量守恒定律(Naive-Stokes方程)来描述水流。此外，被研究的水体为不可压缩流体，紊流的瞬时控制方程如下 [8] ：

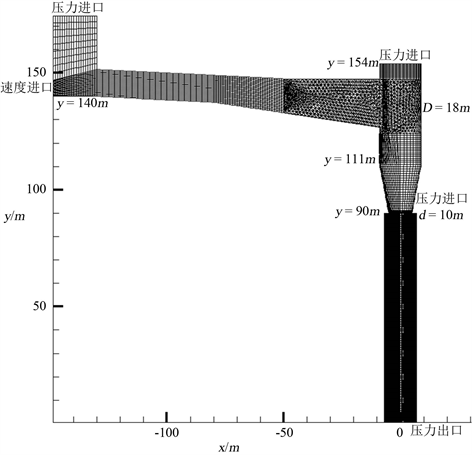
Figure 1. The full wall aeration shaft model

图1. 壁面全程掺气竖井模型

连续方程：

$\frac{\partial \rho }{\partial t}+\frac{\partial \rho {\mu }_i}{\partial x_i}=0$ (1)

动量方程：

$\frac{\partial \rho {\mu }_i}{\partial t}+\frac{\partial \left(\rho {\mu }_i{\mu }_j\right)}{\partial x_j}=-\frac{\partial P}{\partial x_i}+\frac{\partial }{\partial x_j}\left[\left(\mu +{\mu }_t\right)\left(\frac{\partial {\mu }_i}{\partial x_j}+\frac{\partial {\mu }_j}{\partial x_i}\right)\right]$ (2)

k方程：

$\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho {\mu }_{i}k\right)}{\partial x_i}=\frac{\partial }{\partial x_i}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_i}\right]+G-\rho \epsilon$ (3)

ε方程：

$\frac{\partial \left(\rho \epsilon \right)}{\partial t}+\frac{\partial \left(\rho {\mu }_i\epsilon \right)}{\partial x_i}=\frac{\partial }{\partial x_i}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\partial \epsilon }{\partial x_i}\right]+C_{1\epsilon }\frac{\epsilon }{k}G-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}$ (4)

式中：r为流体的密度，t为时间；μ_i、μ_j为速度分量；x_i、x_j为坐标分量；μ为分子黏度系数；P为修正压力；s_k、s_e分别为k、e的紊流普朗特数，C_1e、C_2e为e方程常数，G为平均速度梯。

确定自由液面采用体积率函数法(VOF)，粘性底层选择标准壁面函数法处理。计算采用有限体积法隐格式迭代式算法求解，并利用PISO算法计算压力场与速度场的耦合。

整个计算体的边界条件见图1，入口设置为速度进口，可通过给定不同的流速来控制总流量。入口顶部水平向设置一个压力进口断面，压力值为大气压力。涡室顶部、收缩段与竖井段衔接处的环形区域同样设置为压力进口，这是由于一方面为了保证通气量，另一方面这两个平面均是垂直于铅直方向的平面，而水流受重力整体往下流动，设置为压力进口对控制体内质量守恒基本无影响。现重点探讨竖井边壁纵向掺气坎处的边界条件：一方面，该断面是掺气断面，若边界条件设置为墙体，则空气无法进入竖井中达到掺气效果；另一方面，旋转的高速水流冲击壁面后，会产生回水，如若边界条件设置为压力进口，则会有一部分水流经过该断面流出整个模型，这样一来不能保证模型内部水流质量守恒，效果不佳。故此，本文提出：自y = 80 m高程起，每相距10 m设置两个对称分布延伸出掺气坎的通气井。如此以来，既达到了补气的要求，也不会使得水流流出计算区域，并更贴近于实际工程情况。

4. 水流流态与压强分析

本文讨论纵向壁面掺气坎的位置布设，在与入口来流方向一致的对侧布设掺气坎的基础上，又计算了将对称掺气坎逆时针旋转30˚、60˚、90˚、120˚、150˚五个不同情形，结果表明其水流流态与压强特性基本一致，在此不作分别赘述，现针对流量为1214 m³/s工况进行分析。

为了更好的看清楚进入涡室后内部水流流态，沿竖井中轴线纵向剖出4个等分竖井的断面，断面位置布置如图2，各断面详细水气分布云图如图3。从图3可以明显看出，水流流入涡室后旋转流动，在涡室与收缩段内部形成了竖直方向贯通的空腔，且水流在整个竖井直段中贴壁往下继续旋流。选取y = 88、75、51 m高程处作出横剖面水气分布云图，从图4中不难发现：水流从收缩段流入竖井直段时，突扩形成环形掺气空腔过程中会脱壁流动一小段距离，此后冲击竖井直段壁面而形成一个主流冲击区，产生了少量回水，但始终保持了持续的空腔存在。在顺进口水流方向布设对称壁面掺气坎的情况下，主流冲击区坐落于近进口端一侧掺气坎附近，导致此处掺气坎被淹没，而远进口端壁面掺气坎可形成稳定空腔。尔后，水流进一步往下旋流，原淹没一侧掺气坎空腔渐显，而原形成了稳定空腔的掺气坎空腔减小。在竖井直段内水流旋转流动过程中，经纵向壁面掺气坎处亦会发生脱壁现象，形成掺气空腔，产生少量回水，此处回水在空腔区贴紧壁面垂直向下跌落，如此一来，保证了水流充分掺气，避免空化空蚀现象的产生。

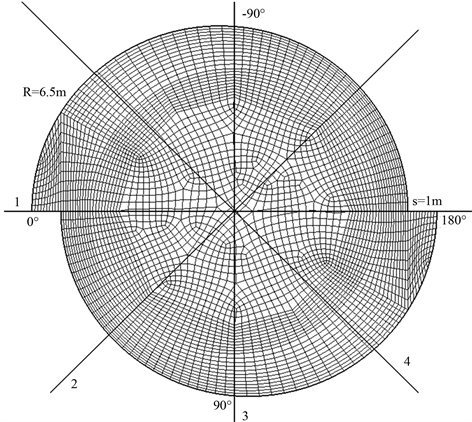
Figure 2. y = 85 m cross-section grid chart

图2. y = 85 m处横剖面网格图

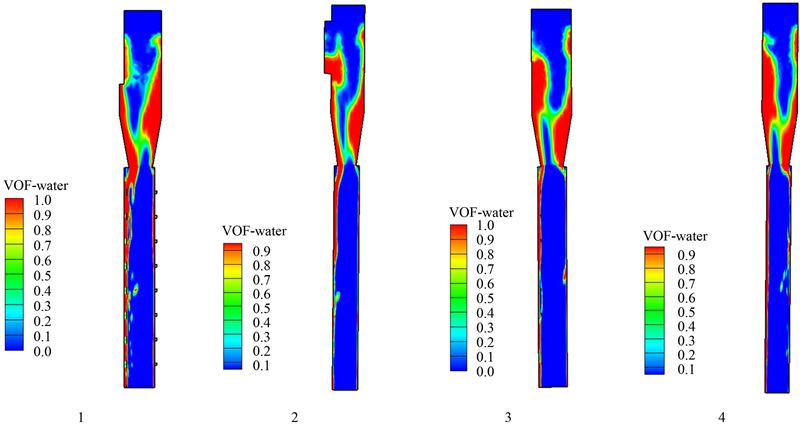
Figure 3. The vertical section of the shaft moisture distribution cloud chart

图3. 竖井纵向剖面各断面水气分布云图

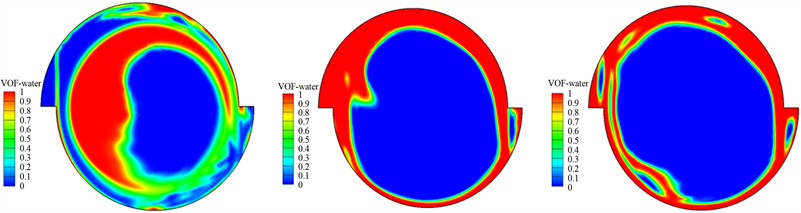(a) y = 88 m (b) y = 75 m (c) y = 71 m

Figure 4. Different elevation cross-section moisture distribution cloud chart

图4. 不同高程横向剖面水气分布云图

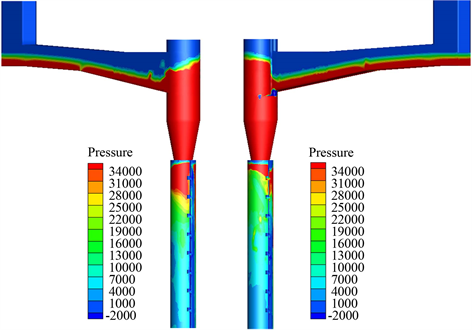
竖井的稳定性与壁面压强密切相关，作出竖井外壁面压强云图。从图5中可以明显看出，涡室与收缩段壁面压强较竖井段大，竖井段壁面压强随着高程的降低而减小，到竖井直段底部壁面压强显著降低。产生如是现象是因为：水流在涡室和收缩段中流动时，由于来流流速较大，且紊动剧烈，离心力的作用使得其紧贴壁面，故而切向速度较大，对壁面冲击力更强。进入竖井段之后，一方面，由于水流发生扩散产生环形空腔的过程中有脱壁流动现象，导致再接触壁面时产生冲击，此处压强明显较大；另一方面，随着环形掺气坎与对称的纵向掺气坎源源不断的掺入空气，对来流产生消能作用，且水流能量随着高程降低，沿程损失量增大，切向速度越来越小，对壁面的冲击力也愈发减弱，故而呈现出在竖井段壁面压强随高程的降低逐渐减小的现象。

本文横向剖出y = 75 m、y = 65 m、y = 55 m、y = 45 m四个代表性截面，做出压强云图进行分析。如图6所示，靠近收缩段与竖井段衔接处水流由于扩散，冲击壁面，导致一侧的掺气坎充满水，出现正压，而另一侧掺气坎出现明显负压区域，随着水流往下流动，两侧掺气坎均逐渐出现负压区。而同一高程的压强分析可见：

(a) (b)

Figure 5. Shaft wall pressure cloud chart. (a) Positive face; (b) Back face

图5. 竖井外壁面压强云图。(a) 正面；(b) 背面

(a) y = 75 m (b) y = 65 m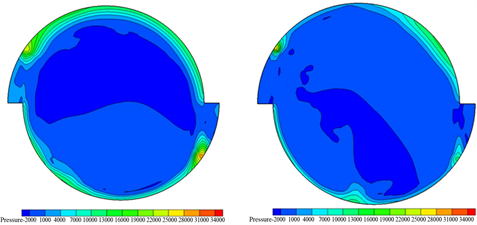(c) y = 55 m (d) y = 45 m

Figure 6. Different elevation cross-section pressure cloud chart

图6. 不同高程横向剖面压强云图

水流流经掺气坎脱壁运动后，再次贴壁流动时会产生冲击区，该区域的压强较大，此后水流继续旋转流动，压强减小。由于整个水流是旋转流动且分别流经两个掺气坎，故此压强分布也不是对称的，主流冲击区一侧压强较大，经过半圈的旋流消能，主流冲击区对侧壁面压强有所降低。

5. 空腔特性及掺气坎位置

整个模型计算后形成了两个明显的空腔区，一个是在收缩段与竖井段衔接处，由于水流发生突扩而形成的环形掺气空腔区；另一个是在竖井直段壁面，由于掺气坎的设置而形成的空腔区。为了更好的观察空腔区的大小，本文采用VOF法，并将水的体积分数调整为0.5，仅分两层进行观察分析。此时水气两者产生明显的分界线，空腔长度则可以通过读点计算求出。对于环形空腔区域而言，由于收缩段与竖井段衔接处位于y = 90 m高程处，故直接用90减去读出的点坐标的y值可即得到该处空腔长度。至于纵向壁面空腔长度，每个横向剖面各点是处于同一高程的，故此在计算时只讨论x、z坐标值。由于纵向掺气坎附近壁面存在回水的情况，则读出与掺气坎垂直方向最大距离的两个点的x、z坐标值，然后利用两点之间距离公式：

$L=\sqrt{{\left(x_1-x_2\right)}^2+{\left(z_1-z_2\right)}^2}$ (5)

作为单侧掺气坎近似的空腔长度。

通过计算可以发现，环形空腔区的大小与壁面掺气坎的布设位置无关，其最大空腔长度约为5.4 m，除极少部分回水紧贴壁面向上回流外，其余部分形成明显的空腔(如图4)。由于整个水流在竖井内部旋转流动，且在突扩处存在主冲击区，所以两侧掺气坎空腔长度存在差异，此时需要将两侧掺气坎分别讨论。选取顺进口水流方向近进口断面处位置为0˚，逆时针旋转方向为正方向(如图2)。当掺气坎布设于0˚与180˚两侧时，由于突扩而下的大股水流集中于0˚附近形成主流冲击区，导致该处空腔被完全淹没，不过随着水流继续往下流动，空腔稍显，但很快又被淹没；其他布设不同位置壁面掺气坎时也总有一侧发生该似情况。空腔区域不明显一侧掺气坎研究意义不大，故仅选择布设不同位置情况下，能够全程形成明显空腔的一侧掺气坎进行研究分析。

作出不同位置掺气坎空腔长度沿竖井直段高程变化规律图，从图7中可以看出：当壁面掺气坎布设于180˚处时，空腔长度明显小于布设于其他位置处；当布设于90˚位置时，可以获得最大空腔长度。这是由于水流进入竖井直段之前的突扩，导致形成一个主流冲击区，该区域主要分布于−90˚位置附近，故此，布设于−180˚至0˚的掺气坎容易被大股水流冲击导致空腔不明显，故此考虑将布设两道对称掺气坎调整为布设一道掺气坎的情形；而0˚至180˚这个范围内与主流冲击区位置相对较远，且90˚的位置呈现出的空腔长度明显长于其他位置，故此该道掺气坎布设于90˚处为最佳(L：掺气空腔长度，s：掺气坎宽度)。

为了证实这一点，便计算了相同流量下，于进口来流方向近入口断面一侧壁面逆时针旋转90˚的位置布设一道掺气坎的情况。从图8布设单坎的水气分布云图可见，此处布置单坎时，整个竖井直段的不同高程处均可以形成较大且明显的空腔，效果理想。

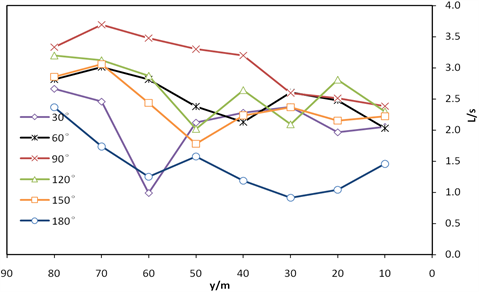
Figure 7. Variation of cavity height along aerator straight section in different positions

图7. 不同位置掺气坎空腔长度沿竖井直段高程变化规律

(a) y = 85 m (b) y = 55 m (c) y = 35 m

Figure 8. Single aeration step with different elevation cross-section moisture distribution cloud chart

图8. 单坎不同高程横向剖面水气分布云图

6. 结论

壁面纵向全程掺气旋流竖井水流进入竖井直段时，主流冲击区易导致掺气空腔不明显。针对这一现象，本文采用数值模拟的方法，建立了一个精度较高的计算体型，研究了不同布设位置的壁面掺气坎，并且对竖井内部水流水力特性进行了分析。结果表明：无论纵向壁面掺气坎布设于何处，竖井内部水流流态均良好，壁面压强沿程未出现异常分布，壁面掺气坎位置对水流流态与壁面压强无明显影响。由于存在主流冲击区淹没掺气坎空腔的情况，故布设一道掺气坎为宜。壁面掺气坎布设于进口来流方向近入口断面一侧逆时针旋转90˚的位置时，空腔长度最大且空腔沿程均稳定贯通。这一结论对今后在实际工程中，采用竖井直段壁面掺气坎消能方案时，掺气坎建造位置的选取具有一定参考价值。