基于LINGO的梯级水坝系统选址优化建模

Location Optimization Modeling of Cascade Dam System Based on LINGO

摘要: 梯级水坝系统能够对水能进行梯级开发，达到河流水力资源的合理开发和综合利用的目的。本文以卡里巴大坝为例，假定将原有水坝改建为梯级水坝系统。在获得赞比西河中游河段卫星高程数据后，利用地理分析软件得到其中数百公里河段有条件建立梯级水坝的地点及相关地理信息。在利用线性回归拟合模型分析数据误差后，论文利用分析软件筛选出千余组水坝可能选址地点的河流截面和库容数据。最后，利用层次分析法建立了综合评价目标函数，并建立线性优化模型利用软件对水坝选址方案进行优化求解，得到成本和经济效益均超越原有大坝的优化解集。本文的研究方法对水利系列的开发有较大的借鉴意义。

Abstract: The cascade dam system can be used in hydropower cascade development to achieve the purpose of rational development and comprehensive utilization of river water resources. Taking Kariba dam as an example, this paper assumed that the original dam will be converted into a cascade dam system. After obtaining the satellite elevation data of the middle reaches of the Zambezi River, the geographic analysis software was used to obtain the location and related geographic information of the cascaded dams where hundreds of kilometers of them were conditionally constructed. After using the linear regression fitting model to analyze the data error, the paper screened out the river cross section and the reservoir capacity data of the possible locations of the dam of a thousand dams by using the analysis software. Finally, the analytic hierarchy process was used to establish the objective function of the comprehensive evaluation, and the linear optimization model was established to optimize the solution of the dam site selection by software. The optimal solution set was obtained which surpasses the original dam with the cost and economic benefits. The research method of this article is of great reference to the development of water conservancy series.

1. 引言

美国大坝安全委员会(Association of State Dam Safety Officials)指出，大坝的平均寿命为50年，NID数据库中确定的美国大坝中有1/4的大坝寿命已经超过了50年。由于建坝时间过长，于“大坝建设的黄金时期(1950~1970)”完工的大量坝体安全问题不断增多，一旦溃坝将会对下游地区造成灾难性影响。随着水电发展“十二五”规划的推进落实，大型流域梯级水库系统将逐渐形成，其联合调度必将获得巨大的电力补偿效益和水文补偿效益，对缓解能源短缺、落实科学发展观、贯彻国家“节能减排”战略以及履行减排承诺均具有重要的理论指导意义和工程实用价值 [1] 。而本文将以世界库容量排名首位的卡里巴大坝为范本，将梯级水坝系统应用于赞比西河卡里巴水库上下游流域，建模分析其选址位置，并进行优化。

经过对赞比西河流域的数据分析，对于赞比西河上中下游的水利开发价值评估方面，本文可以得出以下结论：

1) 赞比西河上游河段：自河源至维多利亚瀑布为其上游河段，长1285 km，主要流经高原地带，河道多弯曲、纵坡缓、水流缓慢，基本不具备水力开发价值。

2) 赞比西河中游河段：自维多利亚瀑布往下游，沿赞比亚与津巴布韦边境直至莫桑比克境内的卡奥拉巴萨为干流中游河段，长约870 km，该段大部分河道切过砂岩层，部分河段切过玄武岩层，水流缓急依河流宽窄而变化，多瀑布及峡谷急流，落差达670 m (未包括维多利亚瀑布)，水电资源非常丰富，开发条件非常好。

3) 赞比西河下游河段：卡奥拉巴萨以下直至河口为干流下游河段，长约580 km。卡奥拉巴萨水库拦河坝以下约70 km长为峡谷河段，河道宽约100~430 m，落差约70 m，水流湍急，两岸山体雄厚，与河谷高差一般为100~380 m，水电资源丰富，开发条件好。其之下约150 km河段河道受两岸地形制约，开发条件较差或不具备开发价值 [2] 。

2. 梯级水坝系统能力分析

2.1. 梯级水坝系统分布状态分析

梯级水坝系统指的是从河流某段开始，从上而下拟定一个河段接一个河段的小型水坝组成的、呈阶梯状分布形式的水利枢纽系统 [3] 。它在水头利用上能够做到分级开发、分段利用，在水量利用上做到多次开发、重复利用。梯级水坝系统在发电量方面理论上是原卡里巴发电站难以比肩的，于是本文希望梯级水坝系统在水资源管理的泄洪能力与原卡里巴水库能力持平的情况下，能创造更高的经济效益。

2.2. 梯级水坝系统中各水库库容关系分析

卡里巴水库作为世界最大的蓄水库之一，其周边形成了众多的产业链和城镇用水关系。基于这些因素的存在，梯级水坝系统不允许原水库消失或完全失去其原有作用。为了满足该实际条件，卡里巴大坝原址堤坝不能被完全拆除。在下文中本文将这个有着特殊意义的水坝称为“原址坝”，并改建该坝为漫水坝。当发生极端洪涝情况时，原址坝难以达到“卡里巴大坝”的强大泄洪以及储蓄能力，直接表现就是超过年均水位的大量水体将漫过原址坝冲向下游，这时就需要梯级水坝系统中的其他组成坝承担起存蓄该部分溢出水体的任务。

亦即从数值上来看，水坝系统的若干水库的最大总库容应在考虑修建成本的前提下等于或超过原卡里巴水库总库容。而在丰水期到来时新系统在水资源管理的洪水积蓄能力方面将与原卡里巴水库达到同一层次。

2.3. 多水坝水利系统中各水坝作用分析

建立水坝的作用就是拦高补低，即在洪水期蓄水，减少下游发生洪灾的可能性；在旱季放水，补充河流，使河道中水流不至于太少。

总体来说，卡里巴大坝建成后，下游的水量会减少，但是由于水库的调节作用，全年河流下游水流会比较平稳，流速减慢。而在大坝上游，受水库影响，水库所在河段水位明显上升，而以原水库河段作为侵蚀基准面的流域内高差减小，流速减缓，这会对河流以及其中的生物等产生影响，从某种程度上来讲，水库的蓄积的调控不当也会造成地下水位的升高，加剧上游的内涝。对于水库自身来说水库的修建从长期来看容易引起泥沙淤积，严重影响水库寿命期 [4] 。

为了避免这些问题，水坝系统采用以下策略：

1) 降低卡里巴大坝原址水坝的高度至近十年的年平均水位。目的是为了减小大坝两端的高度差，提高大坝的稳定性，减轻其压力，并将减轻的压力分散到梯级水坝系统的其他水坝上。

2) 通过对卡里巴湖上下游的精确高程数据分析，本文得到的结论是：梯级水坝系统中的下游水坝应主要承担原卡里巴大坝的蓄水量，由于高度差较小以及水流速度较小的原因，发电机组方面应考虑减少安装。而上游水坝承担少量蓄水任务，主要承担发电和拦沙的任务。

3. 数据收集

高程数据的收集是利用软件BIGEMAP地图下载器锁定相关点坐标，本范例获取了赞比西河从卡里巴大坝(东经28˚45'43.10，南纬16˚31'20.79)至(东经30˚28'30.1144，南纬15˚38'20.3040)流域和维多利亚瀑布(27˚1'5.4737E，17˚57'4.7648S)至卡里巴水库西段(25˚51'3.2032E，17˚56'30.1579S)的精确高程DEM图。

河宽因为没有官方数据，在软件Geogle Earth中利用“标尺”工具获得相关数值。

其中高程数据导入软件Global Mapper中进行后续处理，生成图见图1。

Figure 1. Global Mapper elevation image

图1. Global Mapper高程生成像

4. 数据处理

4.1. 河流平面高程数据处理

由于梯级水电站发电的特性，本文需要了解卡里巴湖下游流域的河流平面高程。其中下游部分数据经过Global Mapper的处理后本文可以得到赞比西河在该流段的纵截剖面图见图2。

该部分数据共1254组(其中卡里巴水库上游部分200组，下游部分1054组)，每一组中有两个数据分别为该观测点海拔高度和该观测点与上一个观测点沿河的长度。在赞比西河该流段河流长度与水面的海拔高度可以大致的看作一元一次函数，于是本文建立了线性回归函数模型，并对该部分数据进行误差分析，线性回归模型为：

$H={\beta }_0+\beta D$ (1)

式中： $H_i$ ——第i组观测点水坝高出河流平面部分的高度；

$D_i$ ——第i组观测点沿赞比西河到原址坝的长度。

利用Matlab软件中的regress函数对该组数据进行处理，得到参数值为： ${\beta }_0=395.54$ ； $\beta =0.00025817$ ；拟合方差为91.361，拟合优度为0.83，误差在可接受范围内。

得到的线性回归模型函数为：

$H=395.54-0.00025817D$ (2)

利用该模型，本文可以得到每一个观测点的河床高度数据。

由官方发布的图片资料如图3所示，本文可以推测出观测起始点的河床高程为380米，那么河床数据的变化应顺应河面高程数据趋势，即本文可以得到河床高程与观测点沿赞比西河到原址坝距离的函数为：

$H{S}_{0i}=380-0.00025817D_i$ (3)

式中： $H{S}_{0i}$ ——下游第i组观测点河床高程值；

同样的，本文可以使用同样的模型，计算出卡里巴湖上游部分156 km河段河床高程与观测点沿赞比西河到维多利亚瀑布的函数为：

$H{U}_{0i}=780-0.002947603D_i$ (4)

式中： $H{U}_{0i}$ ——上游第i组观测点河床高程值。

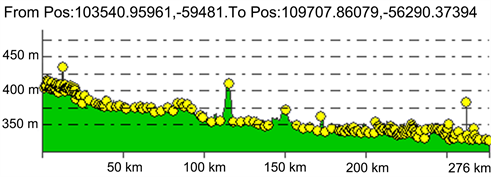
Figure 2. Elevation section of the river plane

图2. 河流平面高程纵截剖面图

Figure 3. Concept map of Kariba dam

图3. 卡里巴大坝泄洪概念图

4.2. 水坝选址与库容的理想化计算模型

本文利用ArcGIS地理分析软件处理赞比西河中游河段卡里巴大坝至东经30˚28'30.1144，南纬15˚38'20.3030位置约276.34 km河段的精确高程DEM图，可以得到1054组观测点分别对应的河岸宽度，其中在前21 km (共102个观测点)和之后的河段(共952个观测点)河宽有较明显区别，部分数据见表1。

本文可以根据以上数据，计算出第i个观测点的河流截面积以及水库在原有河面以上的库容。

如图4所示，水坝高度可以被表示为：

$h_{0i}=H_i+h_i-H_{0i}$ (5)

式中： $h_{0i}$ ——第i组观测点水坝坝高；

$h_i$ ——第i组河流水面高程值；

$H_{0i}$ ——第i组观测点河床高程值。

水库总库容：

Table 1. River wide data of the observation point

表1. 部分观测点河宽数据

Figure 4. Schematic diagram of cross section of a dam

图4. 水坝横截面示意图

$\begin{array}{l}{S}_{1i}=\frac{1}{2}{L}_i^2\arccos \left(\frac{R_i-h_{0i}}{R_i}\right)-\frac{1}{2}\left(R_i-h_{0i}\right)\sqrt{2R_i{h}_{0i}-h_{0i}^2}\\ S_{2i}=L_i^2\left(\frac{1}{8}\text{π}-\frac{1}{4}\right)\\ S_{3i}=S_{1i}-S_{2i}\end{array}$ (6)

式中： $S_{1i}$ ——第i组观测点总库容横截面积；

$S_{2i}$ ——第i组观测点河流横截面积；

$S_{3i}$ ——第i组观测点水库的原河上方库容横截面积；

$L_i$ ——第i组观测点的河宽；

$R_i$ ——第i组观测点的河底圆弧半径。

如图5所示，则第i组观测点下辖河面部分库容计算模型为：

$V_{U,i}=S_{1i}\cdot D_i$ (7)

式中： $V_{U,i}$ ——第i组观测点下辖河面部分库容。

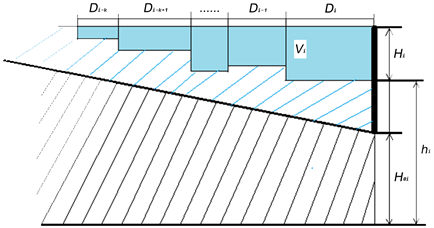
Figure 5. Schematic diagram of reservoir capacity

图5. 水库库容示意图

本文把河面阶梯化以便于计算，第i个观测点水坝的水库大小将取决于前k个观测点的河面高度，如上图所示，该水库长度是k个观测点河面以上部分库容之和。则河面以上部分库容计算模型为：

$V_i={\displaystyle \underset{j=i-k}{\overset{i}{\sum }}{V}_{U,j}}={\displaystyle \underset{j=i-k}{\overset{i}{\sum }}{S}_{1i}\cdot D_i},\left(i>1,i\in Z\right)$ (8)

式中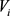：——第i组观测点水库的原河上方库容量。

5. 水坝系统线性优化模型

5.1. 目标函数的确立

1) 成本尽量低：本文使用兴建水坝的总截面面积的概念，去近似替代在水坝系统的建造成本中占比最大的工程材料费用 [5] 。

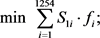(9)

2) 蓄水量(总库容)尽量大：在成本可控的条件下，更大蓄水量意味着汛期到来时更高的安全指数。

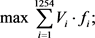(10)

3) 本文寻求在成本尽可能低、蓄水量尽可能大、兴建水坝数量尽可能少三个方面之间的平衡，这里利用层次分析法建立综合评价目标函数Q(x)，通过对当地具体情况的分析，本文建立比较矩阵如表2所示。

最大特征根的归一化特征向量：

(11)

一致性检验：

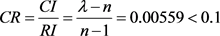(12)

由检验结果可知该模型的误差在容许的范围内，将权重值代入综合评价目标函数，可得：

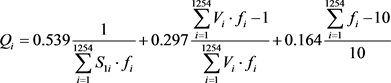(13)

式中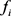：——0-1变量，表示第i个观测点在水坝系统是否确认为修建点。

Table 2. Comparison matrix data

表2. 比较矩阵数据

5.2. 约束条件的确立

1) 修建的水坝在河面以上的总库容应大于极端条件下的原卡里巴水库泄洪总量：

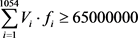(14)

2) 由于梯级水坝系统所占据的河段较长，且水坝个数过多会对生态环境等各方面造成不利的影响，为了权衡水库经济效益和环境影响，本模型中梯级水坝系统兴建的水坝总量应介于10到20之间：

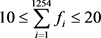(15)

3) 使用0-1变量矩阵f表示第i个观测点在水坝系统中是否确认为修建地：

(16)

5.3. 优化模型的建立与求解

本文将第一小节中的三个目标分别作为最优先目标，将数学模型转化为程序语言利用Lingo软件求解，在这里用成本、蓄水量和综合指标代替，得到最优方案如表3所示。其中，由卡里巴大坝兴建历史上汛期的最大泄水量为1978年测量的65,000,000立方，库容优化倍数是指每种方案所得到的梯级水坝系统总库容与该最大泄水量的比值。

对目标为水坝系统综合目标时，本文建立的优化模型为：

具体最优解集见表4。模型给出的水坝兴建数为20个，总库容为104,739,521立方米，截面总面积411,527平方米，目标函数值为0.4610013。梯级水坝系统能够提供原大坝1.6倍的泄水库容。证明梯级水坝优化计算方案可行。

Table 3. Comparison of optimal solutions under different priorities

表3. 不同优先目标下的最优方案比较

Table 4. LINGO programming optimal solution set

表4. LINGO编程得到的最优解集

6. 结语

世界上存在很多水库隐患问题，隐患问题又有诸多分支，本文很难对这样一个范围极大且分类众多的问题直接进行建模分析。但是本文选取极其具有代表性的隐患水坝，去进行第一部分的建模分析。通过这种分析，可以由点即面，建立适应各地水坝分析的数学模型，以便于研究的顺利进行。本文的计算过程中存在一些理想化假设，数据获取时因为具体情况过于复杂而存在一定的不精确性，这对结果会造成一定的影响，在这方面，还有待进一步的细化和研究。

基金项目

2017年上海工程技术大学校级大学生创新训练项目(cx1706004)。