调水工程对调蓄水库水温影响的研究

Effect of Water Transfer Project on Regulating Reservoir Water Temperature

摘要: 调水工程是解决地区水资源不足或时空分布不均衡问题的必要工程措施，不同水库间通过管道和河流调水会对调蓄水库水温产生影响。采用二维水流水温数学模型模拟了吉林省引松供水工程调水对调节水库石头口门水库水温的影响。计算结果表明，调水对调蓄水库水温影响的范围、时间主要和调水量、调水温差、水库水深、入水口位置等有密切关系。引松供水工程调水量和调蓄水库的水量相比很小，调水对水库水温分布的影响有限。调水入水口位于库尾，受影响的范围基本局限于水库库尾局部范围内，水温影响在1个月内即达到平衡，对整个库区和坝前影响很小。调水工程入水口远离坝址可以减小调水对调蓄水库及下游河流的影响程度。

Abstract: Water transfer project is the necessary engineering measure to solve the problem of insufficient water resources or the imbalanced spatial and temporal distribution problems. Water diversion between dif-ferent reservoirs through the pipeline and river will affect the reservoir water temperature. The two-dimensional hydrodynamic-thermal mathematical model is used to simulate the influence of the Jilin Province Water Diversion Project on the water temperature of Shitoukoumen Reservoir. The results show that the effect of the project to the range and time of the reservoir water temperature regulation is closely related to the amount of water transferred, the water temperature difference, the water depth of the reservoir and the position of the water inlet. The water amount of Jilin Province Water Diversion Project is very small compared with that of the storage reservoirs, and the influence of water diversion on the water temperature distribution in the reservoir is limited. The water diversion inlet is located at the end of the reservoir. The affected area is basically limited to the local area of the reservoir tail. The impact of water temperature reaches equilibrium within one month, with little impact on the whole reservoir area and the dam. Water diversion project away from the dam site can reduce the impact of the reservoir and downstream rivers.

1. 引言

我国许多地区由于特定的地理条件，水资源时空分布很不均衡，导致地区工程性缺水、资源性缺水或水质性缺水。往往需要通过调水工程来有效利用和调配水资源。如南水北调、引江济淮、引黄入晋工程等都属于大型的跨流域调水工程。在调水工程中，必须具有足够水量的调蓄水库来保证调度运行的灵活性和便捷性。调水工程的实施必然会对调蓄水库水环境及其下游河道产生影响，许多学者都对调水工程的生态环境影响进行了研究 [1] [2] [3] [4] 。

随着工农业用水对水质要求的提高，调蓄水库除了调节水资源量外，还要兼顾调水对灌溉、渔业的影响，这些都和水库水温关系密切。一旦调水水量过大，调水水温过高或过低达不到生态用水温度要求，将会引起灌溉农作物大幅度减产，同时对下游河道中的水生生物特别是鱼类产生毁灭性打击。如刘建康、蒋固政的研究表明，春夏季节水库下泄水温低于建库前天然河道水温，将直接导致下游鱼类繁殖季节推迟、当年幼鱼生长期缩短、生长速度减缓 [5] [6] 。韩彩霞、吴佳鹏研究了水库下泄水温对农作物的影响，如果下泄水温未达到最适宜温度范围，将使得灌溉难以发挥最佳效益 [7] [8] 。因此，准确预测调水对调蓄水库水温分布的影响十分必要。

20世纪60年代初美国最先开始研究水库水温的分布和变化规律。此后，许多学者采用不同种方法和手段对水库库区水温分布进行大量研究工作，取得了许多有意义的成果。如刘平等 [9] 通过经验公式法对迪那河五一水库水温及下泄水温进行了预测分析。脱友才、杨红秀分别对丰满水库和汾河水库不同季节的水温变化分布规律进行了原型观测和资料分析 [10] [11] 。赵一慧、甘衍军等 [12] [13] 通过EFDC数学模型模拟了小浪底、二滩水库的水温分布变化规律。江春波、戴凌全等 [14] [15] 对水库水温数学模型研究进展进行了综述，指出了不同模型的优缺点以及需要进一步研究的方向。李林等 [16] 通过三维水温模型研究了支流影响下的水库水温变化特征，表明支流入流越靠近坝址对坝前水温分布影响越大。高学平、柳海涛等 [17] [18] 通过水温模型试验模拟了糯扎渡水库等大型水库的水温分布规律。

本文通过水流水温数学模型，研究了吉林省引松供水二期工程调水对石头口门调蓄水库水温的影响，为工程实施提供技术支撑，对类似调水工程设计具有借鉴意义。

2. 工程概况

吉林省中部城市引松供水工程位于吉林省中部，主要工程措施是从第二松花江丰满水库库区引水至吉林省中部地区，增加向长春、四平、辽源等城市群的生产生活供水，可为退还被城市用水挤占的农业用水和河道生态环境用水、限采地下水创造条件，为中部城市群的振兴和发展提供水资源保证，并改变部分地区的饮用水水质，对保障吉林省百亿斤粮食生产和饮水安全、促进地区乃至全省经济社会可持续发展、改善生态环境具有重要作用。

依据总体规划，考虑工程的实施进度安排，现状基准年采用2013年，近期水平年为2020年，设计水平年为2030年。设计水平年多年平均引水量为8.98亿m³，丰满水库取水口设计引水流量为38.0 m³/s。目前吉林引松工程一期工程顺利实施，二期工程正在方案论证阶段，共包括12条输水支线和1座调蓄水库为石头口门水库，通过在总干线设立饮马河分水口向石头口门水库调水。

饮马河是第二松花江较大的一条支流，发源于磐石市驿马乡呼兰岭，流经磐石、双阳、永吉、九台、德惠、农安六县(市)，至农安县靠山屯与伊通河汇合，北流近20公里汇入第二松花江。饮马河分水口距离石头口门水库约40 km，调水所经河道弯曲，河槽较浅，河底为细沙和淤泥。汛期流量较大，非汛期流量较小。

石头口门水库供水对象为长春市玉米工业园、九台市、德惠市，水库控制流域面积 4944 km ²，原设计是以防洪除涝、农业灌溉为主，结合发电和养鱼等综合利用的大型水库。兴利增容工程完成后，水库的任务调整为防洪、城市供水、灌溉为主，兼顾发电。正常蓄水位为189.0 m，死水位为182.5 m，兴利库容38,409万m³。图1为饮马河流域及石头口门水库示意图。

Figure 1. Sketchmap of the Yinma River basin and Shitoukoumen reservoir

图1. 饮马河流域及石头口门水库示意图

3. 数学模型的建立

3.1. 水流基本方程

1) 连续方程

$\frac{\partial Z}{\partial t}+\frac{\partial Hu}{\partial x}\frac{\partial Hv}{\partial y}=q$ (1)

2) 动量方程

$\frac{\partial Hu}{\partial t}+\frac{\partial Huu}{\partial x}+\frac{\partial Huv}{\partial y}=-gH\frac{\partial Z}{\partial x}-\frac{\partial H\overline{u^{\prime }{u}^{\prime }}}{\partial x}-\frac{\partial H\overline{u^{\prime }{v}^{\prime }}}{\partial y}+fHv+\frac{{\tau }_{sx}-{\tau }_{bx}}{\rho }+q{u}_{*}$ (2)

$\frac{\partial Hv}{\partial t}+\frac{\partial Huv}{\partial x}+\frac{\partial Hvv}{\partial y}=-gH\frac{\partial Z}{\partial y}-\frac{\partial H\overline{v^{\prime }{u}^{\prime }}}{\partial x}-\frac{\partial H\overline{v^{\prime }{v}^{\prime }}}{\partial y}-fHu+\frac{{\tau }_{sy}-{\tau }_{by}}{\rho }+q{v}_{*}$ (3)

式中： $u$ 、 $v$ 分别为 $x$ 、 $y$ 方向流速分量； $Z$ 为水位； $H$ 为水深； $f=2\omega \sin \phi$ 为科氏力系数(ω为地球自转角速度)； $q$ 为单位面积上的源汇强度(m³/s∙m²)， $u_{*}$ 和 $v_{*}$ 为源汇节点周边 $x$ 、 $y$ 方向流速分量。 $\left({\tau }_{sx},{\tau }_{sy}\right)$ 为表面风应力项， $\left({\tau }_{bx},{\tau }_{by}\right)$ 为底部床面阻力项。

3.2. 二维温水扩散运动方程

$\frac{\partial \Delta TH}{\partial t}+\frac{\partial \left(Hu\Delta T\right)}{\partial x}+\frac{\partial \left(Hv\Delta T\right)}{\partial y}=D{}_{x}H\frac{{\partial }^2\Delta T}{\partial x^2}+D_{y}H\frac{{\partial }^2\Delta T}{\partial y^2}-\frac{k\Delta T}{\rho C_P}+q\Delta T_i$ (4)

式中： $\Delta T$ 为水体的温升(℃)； $\Delta T_i$ 为源项水体超温值(℃)； $D_x$ 、 $D_y$ 为热扩散系数； $k$ 为水面综合散热系数； $C_P$ 为水的比热； $\rho$ 为水体密度(kg/m³)； $q$ 为源项单位面积流量(m³/s∙m²)。

3.3. 求解方法及定解条件

1) 求解方法

采用《海岸与河口潮流泥沙模拟技术规程》(JTS/T 231-2-2010)推荐的三角形单元法进行方程的离散和求解，采用Fortran计算机语言进行实际编程计算。

2) 初始条件

初始条件的影响将会在经过几次迭代后逐渐消失，因此本文采用冷启动来处理。即给定初始条件时刻计算域内所有求解变量为定值。

3) 边界条件

开边界水动力计算给定潮位过程。

温升计算边界出流时给定：

$\frac{\partial \left(D\Delta T\right)}{\partial t}+\frac{1}{C_{\xi }{C}_{\eta }}\left[\frac{\partial }{\partial \xi }\left(D\Delta Tu{C}_{\eta }\right)+\frac{\partial }{\partial \eta }\left(D\Delta Tv{C}_{\xi }\right)\right]=0$ (5)

温升计算边界入流时：

$\Delta T|{}_{{\Gamma }_0}=\Delta T_a\left(t,\xi ,\eta \right)$ (6)

式中： $\Delta T_a$ 为入流外海边界热回归温升过程，当选取范围足够大，即开边界在温排水扩散范围外时，可认为入流温升为零。

闭边界水动力计算时，流速满足不可入边界条件，即其法向流速为0。温升计算时闭边界采用绝热条件，即温排水扩散法向浓度梯度为0。

4) 动边界

工程水域有大片浅滩，高潮位时淹没，低潮位时出露，计算过程中采用冻结法处理动边界。

3.4. 计算条件

根据调水方案和饮马河基本概况，数学模型计算了1月份、5月份和7月份调水情况下的水库温度变化。其中，1月份调水流量为6.31 m³/s，调水温度为1.7℃，水库温度为0.3℃。5月份调水流量为7.91 m³/s，调水水温为7.5℃，水库水温为12.95℃。7月份调水流量为3.78 m³/s，调水温度为11℃，水库温度为26.5℃。

3.5. 计算参数

根据工程水域实测水温和风况统计，确定计算所需的平均水温和风力条件。在数学模型计算中，影响温度扩散的主要因素是热扩散系数和水面综合散热系数。热扩散系数的取值和温排水的扩散和输移与水流运动有关，一般取热扩散系数为常值，也有学者按沿水流方向和垂直水流方向分别取值。根据已有研究成果，本次计算采用下式计算：取D_x = 0.5 m²/s和D_y = 0.5 m²/s。水面蒸发系数和水面综合散热系数采用《工业循环水冷却设计规范(GBT 50102-2014)》中公式计算确定。图2为水库计算范围和计算网格。

4. 调水影响分析

为了分析调水对水库水温的影响，分别在水库库尾、水库中央和水库坝前(1#、2#和3#点)布置监测点，进行数据提取和分析，监测点位置见图3。

4.1. 监测点水温变化

表1为不同月份监测点水温随时间的变化特征值，图4为1月份监测点水温变化过程。可知，三个月份不同的调水量、调水温度和水库水温情况下，调水只对水库入口局部区域内水温产生影响，水库中部和坝前水温基本不受影响，水温影响在1个月内即达到平衡。这主要是因为水库调水量相对于水库水量非常小，不足以影响整个水库水温。

4.2. 调水水温影响范围

图5为1月份调水后水库在30天内水温的变化分布情况，可以看出由于调水口在库尾，调水量相对于整个

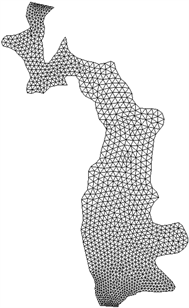
Figure 2. Computational grid of reservoir

图2. 水库计算网格图

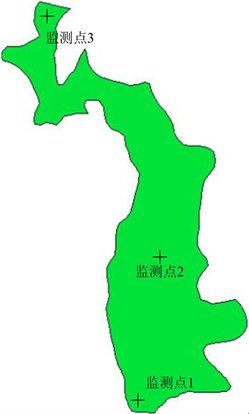
Figure 3. The layout of observation point

图3. 水库观测点布置图

Figure 4. Change of water temperature at observation point in January

图4. 1月份监测点水温变化

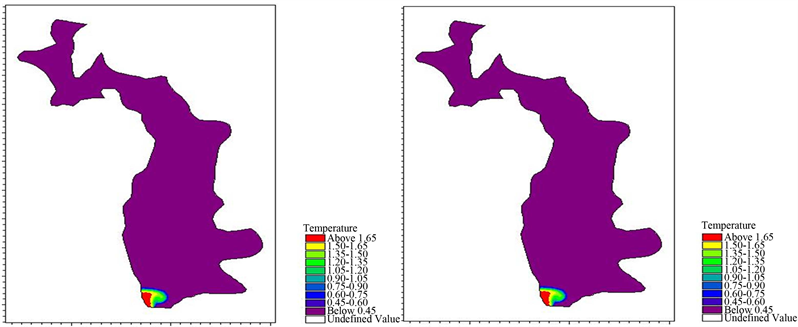5 d 15 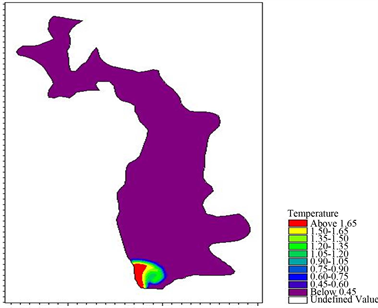d30 d

Figure 5. Variation distribution of water temperature in 30 days in January

图5. 1月份调水后水库30天内水温变化分布

Table 1. Water temperature change at observation point

表1. 水库计算监测点水温变化表

Table 2. Influence distance of water temperature change

表2. 石头口门水库水温影响距离

调节水库的水流非常小，调水对水库水温的影响范围仅限于库尾局部区域。

4.3. 调水水温影响距离

表2为调水对石头口门水库水温的纵向距离，其中1月份调入水的影响距离最远为1945 m，5月份调入水的影响距离最远为1431 m，7月份调入水的影响距离最远为1452 m。不同调水方式下，调水对水库水温的影响主要集中在库尾局部范围内。

5. 结论

本文针对吉林省引松供水二期工程，建立了石头口门水库平面二维水流水温数学模型，预测了水库调水后库区水温的变化情况、影响范围和影响时间等。主要结论如下：

1) 调水对水库水温影响的范围、时间主要和调水量、调水温差、水库水深、入水口位置等有密切关系。

2) 由于调水量和水库水量相比并不大，调水对水库水温分布的影响有限，受影响的范围基本局限于库末局部范围内，水温影响在1个月内即达到平衡。

3) 调水工程入水口位置尽量设置在水库库尾，远离坝址可以防止调水对水库坝前以及下游河流产生影响。

4) 平面二维水流水温数学模型可以对水库调水影响进行合理的模拟预报。但水库水深相对较大时，水温和水库水体的掺混具有典型的三维特征，更精细的预报需要借助于三维数学模型来模拟。

基金项目

国家自然科学基金(51409163, 51479122)；国家重点研发计划(2017YFC0405400)资助。

参考文献