分数阶Oldroyd-B流体在垂直圆柱外的流动和传热

Heat and Mass Transfer of the Generalized Fractional Oldroyd-B Fluid past a Moving Vertical Cylinder

摘要: 本文研究了垂直圆柱外的分数阶Oldroyd-B不可压缩粘弹性流体自然对流传质传热的过程。在描述Oldroyd-B流体的本构关系时引入了分数阶微积分。用L1格式和隐式Crank-Nicolson格式对含有对流项的偏微分方程进行数值离散。最后详细说明和讨论了不同的物理参数对速度和温度的影响。结果表明，部分物理参数对速度分布具有显著的影响，但对温度分布和浓度分布影响不大。

Abstract: This paper studies the heat and mass transfer of an incompressible viscous radiative generalized Oldroyd-B fluid past a moving vertical cylinder. The Caputo fractional derivative operator is in-troduced to describe the constitutive relationship of Oldroyd-B fluid. This partial differential system including convection terms is solved by implicit finite difference scheme of Crank-Nicoson type combined with L1-algorithm.The effects of different physical parameters on the velocity and temperature are illustrated and discussed in detail. The results indicate that these new physical parameters have dramatic influence on the velocity distribution, but little on the temperature and concentration distribution.

1. 引言

众所周知，圆柱体外的热对流在核反应堆冷却系统和地下能源系统等工程和物理领域有着广泛的应用。而且这一概念已经扩展到很多相关的领域 [1] - [15] 。Deka和Paul [1] 研究了运动的无限垂直圆柱外的一维非稳态的自然对流，并得到了精确解。Mukhopadhyay [2] 用打靶法得到了多孔介质中拉伸圆柱上的粘性不可压缩混合对流耗散传热过程的数值解。Takhar和Chamkha [3] 结合热扩散和质量扩散的双重影响，研究了连续移动垂直细长圆柱上的混合对流。此外，对该问题的研究有解析和数值两种方式。例如文献 [4] [5] [6] 和文献 [7] - [15] 分别应用摄动方法和数值方法对该问题进行了研究。

近年来，非牛顿粘弹性流体特别是分数阶粘弹性流体受到越来越多的关注。在对这类问题研究的过程中，分数阶微分算子已被证明是一个很好的研究粘弹性流体的工具，并且提出了很多的分数阶数学模型来描述粘弹性流体的传热传质问题 [16] - [22] 。例如Khan和Hyder [16] 研究了两无限长共轴圆柱体之间的非稳态粘弹性流体的流动，并且用汉克尔变换和拉普拉斯变换得到了精确解。Qi和Jin也做了相似的工作 [17] [18] 。Qi [18] 处理了两无限同轴圆柱之间的广义非定常的Oldroyd-B流体的旋转流，并且在流体的本构方程中引入了分数阶微分算子。Povstenko [19] 用时间分数阶扩散方程描述了径向扩散的圆柱流。Mahmood [20] 研究了两个无限长同轴圆柱间的广义Maxwell流体的震荡流。Mahmood [21] 研究了无限圆柱内的广义二阶流体的旋转流，并用拉普拉斯变换和汉克尔变换得到了速度场和相关的切向应力。Fetecau [22] 研究了无限圆柱体中的分数阶Oldroyd-B流体旋转流。

在粘弹性流体研究过程中，对流项都没有被考虑进去。近年来，Zhao和Zheng等人 [23] [24] [25] [26] [27] 提出了一系列研究在平板上或者在多孔介质中的分数阶粘弹性流体的数学模型和数值方法。他们提出的最重要的方法是如何处理对流项。受他们工作的启发，在本文研究的问题中同样也考虑了对流项，并最终获得带时间分数阶的非线性耦合的方程。隐式Crank-Nicolson差分格式和L1-算法来求解非线性耦合的偏微分方程组。文章的其余内容组织如下：第二部分建立了广义垂直圆柱外的流动传热的数学模型，并且对方程进行了无量纲化；第三部分给出了数值方法的说明，Crank-Nicolson方法结合L1-算法被用来解决这个耦合的非线性方程组；第四部分根据数值结果，讨论了不同物理参数对速度和温度的影响。

2. 物理模型

引入剪切力的分数阶Oldroyd-B模型 [28] :

$\left(1+{\lambda }_1^{\alpha }\frac{D^{\alpha }}{D{t}^{\alpha }}\right)S=\mu \left(1+{\lambda }_2^{\beta }\frac{D^{\beta }}{D{t}^{\beta }}\right)A_1,\left(0<\beta \le \alpha <1\right),$ (1)

其中m表示流体的黏性系数，S是外力张量， ${\lambda }_1,{\lambda }_2$ 分别为松弛时间常数和迟滞时间常数， $A_1$ 是应变张量。

在柱状坐标系中，对应的本构方程可以写为

$\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)S_{xr}=\mu \left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\frac{\partial u}{\partial r},$ (2)

其中r是圆柱的半径，x垂直于r。 $D_t^{\alpha }$ 和 $D_t^{\beta }$ 是Caputo分数阶算子，分别是对时间的a和b阶导数，a阶Caputo分数阶导数定义为 [29]

$D_t^{\alpha }f\left(t\right)=\frac{1}{\Gamma \left(1-\alpha \right)}{\displaystyle {\int }_0^t{\left(t-\eta \right)}^{-\alpha }{f}^{\prime }\left(\eta \right)\text{d}\eta },0<\alpha <1,$ (3)

其中 $\text{Γ}(\cdot )$ 表示Gamma函数。

考虑在半径为 $r_0$ 的垂直圆柱外的不可压缩的广义Oldroyd-B流体的流动。初始时刻，假设圆柱体表面和流体的温度都为 $T_{\infty }$ ,流体的浓度为 $C_{\infty }$ ，当 $t>0$ 时，圆柱表面在垂直方向以速度 $u_0$ 拉伸运动，圆柱体表面的温度和浓度分别为 $T_w$ 和 $C_w$ ，u和v分别为x轴和r轴方向的速度，T和C分别为温度和浓度。则分数阶Oldroyd-B圆柱外的传热传质控制方程为

$\frac{\partial \left(ru\right)}{\partial x}+\frac{\partial \left(rv\right)}{\partial r}=0,$ (4)

$\begin{array}{l}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial r}+{\lambda }_1^{\alpha }\frac{{\partial }^{\alpha +1}u}{\partial t^{\alpha +1}}+{\lambda }_1^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left(v\frac{\partial u}{\partial r}\right)+{\lambda }_1^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left(u\frac{\partial u}{\partial x}\right)-g\beta \left(T-T_{\infty }\right)\\ -g{\beta }^{*}\left(C-C_{\infty }\right)-g\beta {\lambda }_1^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left(T-T_{\infty }\right)-g{\beta }^{*}{\lambda }_1^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left(C-C_{\infty }\right)\\ =\frac{\nu }{r}\frac{\partial }{\partial r}\left(r\frac{\partial u}{\partial r}\right)+\frac{\nu }{r}{\lambda }_2^{\beta }\frac{{\partial }^{\beta }}{\partial t^{\beta }}\left(\frac{\partial }{\partial r}\left(r\frac{\partial u}{\partial r}\right)\right),\end{array}$ (5)

$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial r}=\frac{k}{\rho C_p}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)+\frac{16\delta T_{\infty }^3}{3\rho C_p{K}^{*}}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right),$ (6)

$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial r}=\frac{D}{r}\frac{\partial }{\partial r}\left(r\frac{\partial C}{\partial r}\right).$ (7)

其中 $k,\rho ,C_p,\delta ,K^{*},D$ 分别为导热系数、密度、定压比热容、Stefan–Boltzmann常数、平均吸收系数和质量扩散系数， $g,\beta ,{\beta }^{*},v$ 分别是重力加速度、热膨胀系数、溶质膨胀系数和运动粘度。

初始条件和边界条件为：

$t\le 0:u\left(x,r,t\right)=0,v\left(x,r,t\right)=0,T\left(x,r,t\right)=T_{\infty },C\left(x,r,t\right)=C_{\infty };$

$t\ge 0:u\left(x,r_0,t\right)=u_0,v\left(x,r_0,t\right)=0,T\left(x,r_0,t\right)=T_W,C\left(x,r_0,t\right)=C_W,$

$u\left(0,r,t\right)=0,v\left(0,r,t\right)=0,T\left(0,r,t\right)=T_{\infty },C\left(0,r,t\right)=C_{\infty },r\ge r_0,$

$u\left(x,r,t\right)\to 0,T\left(x,r,t\right)\to T_{\infty },C\left(x,r,t\right)\to C_{\infty },r\to \infty .$

引入无量纲变换：

$u^{*}=\frac{u}{u_0},r^{*}=\frac{r}{r_0},x^{*}=\frac{x\upsilon }{u_0{r}_0^2},v^{*}=\frac{\upsilon r_0}{v},t^{*}=\frac{t\upsilon }{r_0^2},\theta =\frac{T-T_{\infty }}{T_W-T_{\infty }},C^{*}=\frac{C-C_{\infty }}{C_W-C_{\infty }}.$

可以得到无量纲的边界层控制方程(为了表示方便，“*”在文章中均省去)：

$\frac{\partial \left(ru\right)}{\partial x}+\frac{\partial \left(rv\right)}{\partial r}=0,$ (8)

$\begin{array}{l}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial r}+{\lambda }_1^{\alpha }\frac{{\partial }^{\alpha +1}u}{\partial t^{\alpha +1}}+{\lambda }_1^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left(v\frac{\partial u}{\partial r}\right)+{\lambda }_1^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left(u\frac{\partial u}{\partial x}\right)-g\beta \left(T-T_{\infty }\right)\\ -g{\beta }^{*}\left(C-C_{\infty }\right)-g\beta {\lambda }_1^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left(T-T_{\infty }\right)-g{\beta }^{*}{\lambda }_1^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left(C-C_{\infty }\right)\\ =\frac{\nu }{r}\frac{\partial }{\partial r}\left(r\frac{\partial u}{\partial r}\right)+\frac{\nu }{r}{\lambda }_2^{\beta }\frac{{\partial }^{\beta }}{\partial t^{\beta }}\left(\frac{\partial }{\partial r}\left(r\frac{\partial u}{\partial r}\right)\right),\end{array}$ (9)

$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial r}=\frac{k}{\rho C_p}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)+\frac{16\delta T_{\infty }^3}{3\rho C_p{K}^{*}}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right),$ (10)

$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial r}=\frac{D}{r}\frac{\partial }{\partial r}\left(r\frac{\partial C}{\partial r}\right),$ (11)

其中 $Gr=\frac{g\beta r_0^2\left(T_W-T_{\infty }\right)}{v{u}_0},Gc=\frac{g{\beta }^{*}{r}_0^2\left(C_W-C_{\infty }\right)}{v{u}_0},Pr=\frac{\mu C_p}{K},N=\frac{K^{*}K}{4\sigma T_{\infty }^3},S_c=\frac{\upsilon }{D}$ 分别为温度Grashof数、

浓度Grashof数、普朗特数、辐射参数和Schmidt数。

无量纲的初始条件和边界条件为：

$t\le 0:u\left(x,r,t\right)=0,v\left(x,r,t\right)=0,T\left(x,r,t\right)=0,C\left(x,r,t\right)=0;$

$t\ge 0:u\left(x,1,t\right)=1,v\left(x,1,t\right)=0,T\left(x,1,t\right)=1,C\left(x,1,t\right)=1,$

$u\left(0,r,t\right)=0,v\left(0,r,t\right)=0,T\left(0,r,t\right)=0,C\left(0,r,t\right)=0,r\ge 1,$

$u\left(x,r,t\right)\to 0,T\left(x,r,t\right)\to 0,C\left(x,r,t\right)\to 0,r\to \infty .$

3. 数值计算方法

隐式的Crank-Nicolson差分格式和L1-算法被用来求解上述非线性的耦合偏微分方程组。

3.1. 离散化方法

首先对求解区域进行网格划分， $x,y,t$ 是相互独立的变量，相应的网格间距为 $\Delta x,\Delta r,\Delta t$ ，下标 $i,j$ ，上标k分别表示空间点坐标和空间点坐标， $x_i=i\Delta x,r_j=j\Delta r,t_k=k\Delta t$ 。假设方程(8)~(11)在点 $\left(i,j,k\right)$ 处的精确解为 $u\left(x_i,r_j,t_k\right)$ ， $u_{i,j}^k$ 是方程(8)~(11)在点 $\left(i,j,k\right)$ 处的数值解。我们引入L1-算法来离散时间Caputo分数阶导数 $\left(0<\alpha <1\right)$ [30] ：

$\frac{{\partial }^{\alpha }u\left(x_i,t_{k+1}\right)}{\partial t^{\alpha }}=\frac{\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\left(u_{i,j}^{k+1}+{\displaystyle \underset{s=1}{\overset{k}{\sum }}\left(b_s-b_{s-1}\right)u_{i,j}^{k-s+1}}\right)+O\left(t\right),$

其中，

$b_s={\left(1+s\right)}^{1-\alpha }-s^{1-\alpha }.$

控制方程中整数阶的各项离散形式为 [9] ：

${\frac{\partial u}{\partial t}|}_{t=t_{k+\frac{1}{2}}}=\frac{u_{i.j}^{k+1}+u_{i,j}^k}{\Delta t}+O\left(\Delta t\right),$

${v\frac{\partial u}{\partial r}|}_{t=t_{k+\frac{1}{2}}}=v_{i,j}^k\frac{u_{i,j+1}^{k+1}-u_{i,j-1}^{k+1}+u_{i,j+1}^k-u_{i,j-1}^k}{4\Delta r}+O\left(\Delta r\right),$

${u\frac{\partial u}{\partial x}|}_{t=t_{k+\frac{1}{2}}}=u_{i,j}^k\frac{u_{i,j}^{k+1}-u_{i-1,j}^{k+1}+u_{i,j}^k-u_{i-1,j}^k}{2\Delta x}+O\left(\Delta x\right).$

分数阶导数的离散格式为：

$\frac{{\partial }^{\alpha +1}u}{\partial t^{\alpha +1}}\approx \frac{\Delta t^{-\alpha -1}}{\Gamma \left(2-\alpha \right)}\left(u_{i,j}^{k+1}+u_{i,j}^k+{\displaystyle \underset{s=1}{\overset{k}{\sum }}\left(b_s-b_{s-1}\right)\left(u_{i,j}^{k-s+1}+u_{i,j}^{k-s}\right)}\right),$

$\begin{array}{c}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left(v\frac{\partial u}{\partial x}\right)\approx \frac{\Delta t^{-\alpha }}{4\Delta r\Gamma \left(2-\alpha \right)}(v_{i,j}^k\left(u_{i,j+1}^{k+1}-u_{i,j-1}^{k+1}+u_{i,j+1}^k-u_{i,j-1}^k\right)\begin{array}{c}\\ \end{array}\\ +{\displaystyle \underset{s=1}{\overset{k}{\sum }}\left(b_s-b_{s-1}\right)v_{i,j}^{k-s}\left(u_{i,j+1}^{k-s+1}-u_{i,j-1}^{k-s+1}+u_{i,j+1}^{k-s}-u_{i,j-1}^{k-s}\right)}),\end{array}$

$\begin{array}{c}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left(u\frac{\partial u}{\partial x}\right)\approx \frac{\Delta t^{-\alpha }}{2\Delta x\Gamma \left(2-\alpha \right)}(u_{i,j}^k\left(u_{i,j}^{k+1}-u_{i-1,j}^{k+1}+u_{i,j}^k-u_{i-1,j}^k\right)\begin{array}{c}\\ \end{array}\\ +{\displaystyle \underset{s=1}{\overset{k}{\sum }}\left(b_s-b_{s-1}\right)u_{i,j}^{k-s}}\left(u_{i,j}^{k-s+1}-u_{i-1,j}^{k-s+1}+u_{i,j}^{k-s}-u_{i-1,j}^{k-s}\right)).\end{array}$

最后得到差分方程：

$\begin{array}{l}\left(-\frac{-v_{i,j}^k}{4\Delta r}-\frac{1+\frac{4}{3N}}{2Pr\cdot \Delta r^2}+\frac{1+\frac{4}{3N}}{4Pr\cdot \left(1+\left(j-1\right)\Delta r\right)\Delta r}\right){\theta }_{i,j-1}^{k+1}+\left(\frac{1}{\Delta t}+\frac{u_{i,j}^k}{2\Delta x}+\frac{1+\frac{4}{3N}}{Pr\cdot \Delta r^2}\right){\theta }_{i,j}^{k+1}\\ +\left(\frac{v_{i,j}^k}{4\Delta r}-\frac{1+\frac{4}{3N}}{2Pr\cdot \Delta r^2}-\frac{1+\frac{4}{3N}}{4Pr\cdot \left(1+\left(j-1\right)\Delta r\right)\Delta r}\right){\theta }_{i,j+1}^{k+1}\\ =\frac{\left(1+\frac{4}{3N}\right)\left({\theta }_{i,j-1}^{k+1}-2{\theta }_{i,j}^{k+1}+{\theta }_{i,j+1}^{k+1}\right)}{2Pr\cdot \Delta r^2}+\frac{\left(1+\frac{4}{3N}\right)\left({\theta }_{i,j+1}^k-{\theta }_{i,j-1}^k\right)}{4Pr\cdot \left(1+\left(j-1\right)\Delta r\right)\Delta r}+\frac{{\theta }_{i,j}^k}{\Delta t}\\ -\frac{u_{i,j}^k\left({\theta }_{i,j}^k-{\theta }_{i-1,j}^k\right)}{2\Delta x}-\frac{v_{i,j}^k\left({\theta }_{i,j+1}^k-{\theta }_{i-1,j}^k\right)}{}+\frac{u_{i,j}^k{\theta }_{i-1,j}^{k+1}}{},\end{array}$ (12)

$\begin{array}{l}\left(\frac{1}{\Delta t}+\frac{u_{i,j}^k}{2\Delta x}+\frac{1}{Sc\cdot \Delta r^2}\right)C_{i,j}^{k+1}+\left(\frac{v_{i,j}^k}{4\Delta r}-\frac{1}{2Sc\cdot \Delta r^2}-\frac{1}{4Sc\cdot \left(1+\left(j-1\right)\Delta r\right)\Delta r}\right)C_{i,j+1}^{k+1}\\ +\left(-\frac{-v_{i,j}^k}{4\Delta r}-\frac{1}{2Sc\cdot \Delta r^2}+\frac{1}{4Sc\cdot \left(1+\left(j-1\right)\Delta r\right)\Delta r}\right)C_{i,j-1}^{k+1}\\ =\frac{\left(1+\frac{4}{3N}\right)\left(C_{i,j-1}^k-2C_{i,j}^k+C_{i,j+1}^k\right)}{2Sc\cdot \Delta r^2}+\frac{C_{i,j+1}^k-C_{i,j-1}^k}{4Sc\cdot \left(1+\left(j-1\right)\Delta r\right)\Delta r}\\ +\frac{C_{i,j}^k}{\Delta t}-\frac{u_{i,j}^k\left(C_{i,j}^k-C_{i-1,j}^k\right)}{2\Delta x}-\frac{v_{i,j}^k\left(C_{i,j+1}^k-C_{i-1,j}^k\right)}{4\Delta r}+\frac{u_{i,j}^k{C}_{i-1,j}^{k+1}}{2\Delta x},\end{array}$ (13)

$\begin{array}{l}\left(\frac{v_{i,j}^k}{4\Delta r}+\frac{r_1{v}_{i,j}^k}{4\Delta r}-\frac{1}{4\left(1+\left(j-1\right)\Delta r\right)\Delta r}-\frac{1}{2\Delta r^2}-\frac{r_2}{4\left(1+\left(j-1\right)\Delta r\right)\Delta r}-\frac{r_2}{2\Delta r^2}\right)u_{i,j+1}^{k+1}\\ +\left(\frac{1}{\Delta t}+\frac{u_{i,j}^k}{2\Delta x}+\frac{r_1}{\Delta t}+\frac{r_1{u}_{i,j}^k}{2\Delta x}+\frac{1}{\Delta r^2}+\frac{r_2}{\Delta r^2}\right)u_{i,j}^{k+1}\\ +\left(-\frac{v_{i,j}^k}{4\Delta r}-\frac{r_1{v}_{i,j}^k}{4\Delta r}+\frac{1}{4\left(1+\left(j-1\right)\Delta r\right)\Delta r}-\frac{1}{2\Delta r^2}+\frac{r_2}{4\left(1+\left(j-1\right)\Delta r\right)\Delta r}-\frac{r_2}{2\Delta r^2}\right)u_{i,j-1}^{k+1}\\ =\frac{u_{i,j+1}^k-u_{i,j-1}^k}{4\left(1+\left(j-1\right)\Delta r\right)\Delta r}+\frac{u_{i,j-1}^k-2u_{i,j}^k+u_{i,j+1}^k}{2\Delta r^2}+\frac{r_2{A}_6}{4\left(1+\left(j-1\right)\Delta r\right)\Delta r}+\frac{r_2{A}_7}{2\Delta r^2}+\frac{u_{i,j}^k}{\Delta t}-\frac{v_{i,j}^k\left(u_{i,j+1}^k-u_{i,j-1}^k\right)}{4\Delta r}\\ +\frac{u_{i,j}^k\left(u_{i-1,j}^{k+1}-u_{i,j}^k+u_{i-1,j}^k\right)}{2\Delta x}-\frac{r_1{A}_1}{\Delta t}-\frac{r_1{A}_2}{4\Delta r}-\frac{r_1{A}_3}{2\Delta x}+Gr\frac{{\theta }_{i,j}^{k+1}+{\theta }_{i,j}^k}{2}+Gc\frac{C_{i,j}^{k+1}+C_{i,j}^k}{2}+Gr\frac{r_1{A}_4}{2}+Gc\frac{r_1{A}_5}{2},\end{array}$ (14)

$\begin{array}{l}{v}_{i,j}^{k+1}=\frac{v_{i,j-1}^{k+1}-v_{i,j}^k+v_{i,j-1}^k}{2\Delta r}\frac{1}{\left(\frac{1}{2\Delta r}+\frac{1}{1+\left(j-1\right)\Delta r}\right)}\\ -\frac{u_{i,j-1}^{k+1}-u_{i-1,j-1}^{k+1}+u_{i,j}^{k+1}-u_{i-1,j}^{k+1}+u_{i,j-1}^k-u_{i-1,j-1}^k+u_{i,j}^k-u_{i-1,j}^k}{4\Delta x}\frac{1}{\left(\frac{1}{2\Delta r}+\frac{1}{1+\left(j-1\right)\Delta r}\right)},\end{array}$ (15)

其中，

$r_1=\frac{{\lambda }_1^{\alpha }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)},$

$r_2=\frac{{\lambda }_2^{\beta }\Delta t^{-\beta }}{\Gamma \left(2-\beta \right)},$

$A_1=-u_{i,j}^k+{\displaystyle \underset{s=1}{\overset{k}{\sum }}\left(b_s-b_{s-1}\right)\left(u_{i,j}^{k-s+1}-u_{i,j}^{k-s}\right)},$

$A_2=v_{i,j}^k\left(u_{i,j+1}^k-u_{i,j-1}^k\right)+{\displaystyle \underset{s=1}{\overset{k}{\sum }}\left(b_s-b_{s-1}\right)v_{i,j}^{k-s}}\left(u_{i,j+1}^{k-s+1}-u_{i,j-1}^{k-s+1}+u_{i,j}^{k-s}-u_{i,j-1}^{k-s}\right),$

$A_3=u_{i,j}^k\left(-u_{i-1,j}^{k+1}+u_{i,j}^k-u_{i-1,j}^k+u_{i,j}^{k+1}\right)+{\displaystyle \underset{s=1}{\overset{k}{\sum }}\left(b_s-b_{s-1}\right)u_{i,j}^{k-s}}\left(u_{i,j+1}^{k-s+1}-u_{i,j-1}^{k-s+1}+u_{i,j}^{k-s}-u_{i,j-1}^{k-s}\right),$

$A_4={\theta }_{i,j}^{k+1}+{\theta }_{i,j}^k+{\displaystyle \underset{s=1}{\overset{k}{\sum }}\left(b_s-b_{s-1}\right)}\left({\theta }_{i,j}^{k-s+1}-{\theta }_{i,j}^{k-s}\right),$

$A_5=C_{i,j}^{k+1}+C_{i,j}^k+{\displaystyle \underset{s=1}{\overset{k}{\sum }}\left(b_s-b_{s-1}\right)}\left(C_{i,j}^{k-s+1}-C_{i,j}^{k-s}\right),$

$A_6=u_{i,j+1}^k-u_{i,j-1}^k+{\displaystyle \underset{s=1}{\overset{k}{\sum }}\left({\beta }_s-{\beta }_{s-1}\right)}\left(u_{i,j+1}^{k-s+1}-u_{i,j-1}^{k-s+1}+u_{i,j+1}^{k-s}-u_{i,j-1}^{k-s}\right),$

$A_7=u_{i,j+1}^k-2u_{i,j}^k+u_{i,j-1}^k+{\displaystyle \underset{s=1}{\overset{k}{\sum }}\left({\beta }_s-{\beta }_{s-1}\right)}\left(u_{i,j+1}^{k-s+1}-2u_{i,j}^{k-s+1}+u_{i,j-1}^{k-s+1}+u_{i,j+1}^{k-s}-2u_{i,j}^{k-s}+u_{i,j-1}^{k-s}\right).$

3.2. 求解过程

由初始条件，我们可以得到在 $t=0$ 时的指定区域的 $U,V,\theta ,C$ 的值。在任意时间步长，差分公式(12)~(15)中出现的 $U_{i,j}^k,V_{i,j}^k,{\theta }_{i,j}^k,C_{i,j}^k$ 都被当作是常数。特定的i层的每一个内部节点上都构成了可以用Thomas算法求解的三对角线性方程组 [31] 。赵等人也做了相似的工作 [27] 。重复这一过程，在时间步长和空间步长足够小时， $U,V,\theta ,C$ 的最终收敛值近似为方程(12)~(15)的稳态解。

随着时间的增长，若 $U,V,\theta ,C$ 在两个相邻的时间步的值的差的绝对值小于 ${10}^{-4}$ ，就认为解是收敛的，达到稳定状态的解，迭代过程结束。求解空间必须是有限的，因此设置 $X_{\max }=1$ ， $R_{\max }=21$ ，其中 $R_{\max }=21$ 相应于 $r\to \infty$ 。在经过多次试验后，空间网格的空间步长和时间步长分别固定为 $\Delta X=0.02$ ， $\Delta R=0.05$ $\Delta t=0.01$ 。图1给出了不同时间下速度的变化趋势，并且随着时间的增长速度最终会趋于稳定。如图2

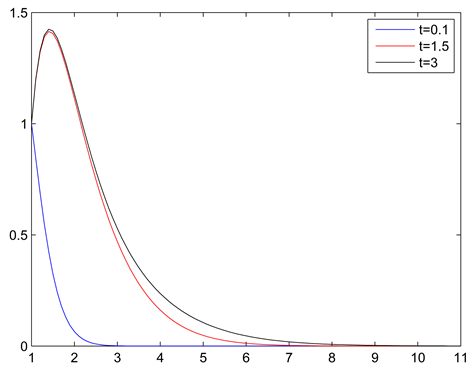
Figure 1. Velocity distribution with increasing time

图1. 随时间增加的速度分布

Figure 2. Velocity distribution for different mesh sizes

图2. 不同网格点下的速度分布

所示，我们使r-方向上的空间步长发生变化，并比较得到的结果，发现数值解的一致性保持良好，因此计算结果与分析是有效的。

4. 分析讨论

4.1. 分数阶导数参数a的影响

图3~图5分别给出了在 $x=0$ 时，不同分数阶导数参数a对速度、温度和浓度的影响。由图像可知，

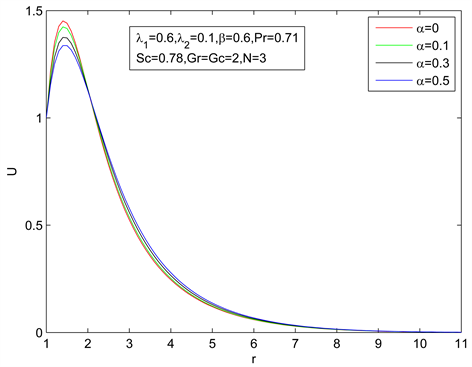
Figure 3. Velocity distribution for different α

图3. 不同α下的速度分布

Figure 4. Concentration distribution for different α

图4. 不同α下的浓度分布

速度曲线不是a的单调函数。对于每一个参数a，速度曲线都有一个与a有关的峰值，并且a越小，峰值越大。对于不同的a值，速度曲线相互交叉。然而，分数阶导数参数a对温度和浓度的影响非常的小，其原因可能是该参数只对剪切力有影响，对传热没有影响。

4.2. 分数阶导数参数b的影响

由图6~图8可以看出参数b对速度、温度和浓度的影响与参数a相似。图6表明，速度首先上升到最大值，然后沿着r的方向不断的减小，最后在远离圆柱的地方趋向于0。此外，速度的最大值随着b的增

Figure 5. Temperature distribution for different α

图5. 不同α下的温度分布

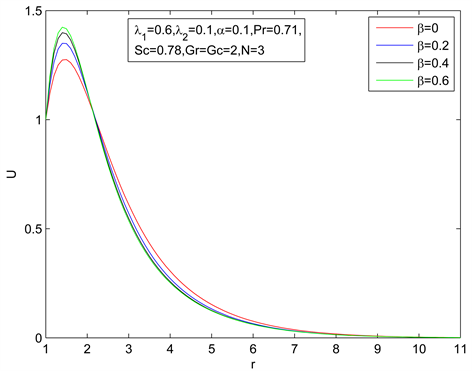
Figure 6. Velocity distribution for different β

图6. 不同β下的速度分布

大而减小。很明显，速度曲线也是相互交叉的。随着参数b的增大，动量边界层的厚度也不断增大。图7、图8表明，分数阶导数参数b对温度和浓度几乎没有影响。

4.3. 松弛时间参数l₁和迟滞时间参数l₂的影响

图9~图14揭示了松弛时间参数l₁和迟滞时间参数l₂对速度、温度、浓度的影响。结果表明，随着松弛时间的变化，速度有明显的变化，特别是在最大值附近。并且最大值是l₁的增函数。速度的最大值是迟滞时间常数l₂的减函数。l₁和l₂对温度和浓度几乎没有影响。

Figure 7. Concentration distribution for different β

图7. 不同β下的浓度分布

Figure 8. Temperature distribution for different β

图8. 不同β下的温度分布

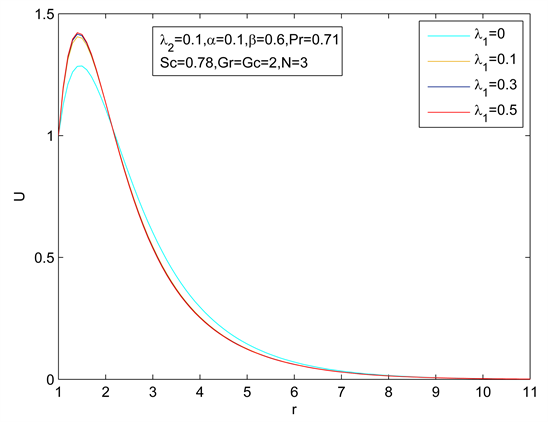
Figure 9. Velocity distribution for different λ₁

图9. 不同λ₁下的速度分布

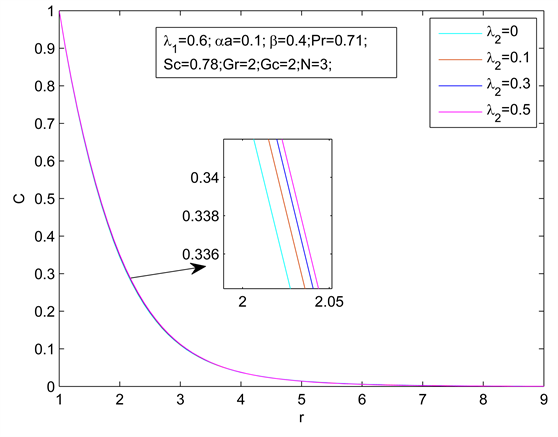
Figure 10. Concentration distribution for different λ₁

图10. 不同λ₁下的浓度分布

5. 结论

本文构建了分数阶Oldroyd-B流体在垂直圆柱外的传质与传热模型，并且用有限差分方法对该问题

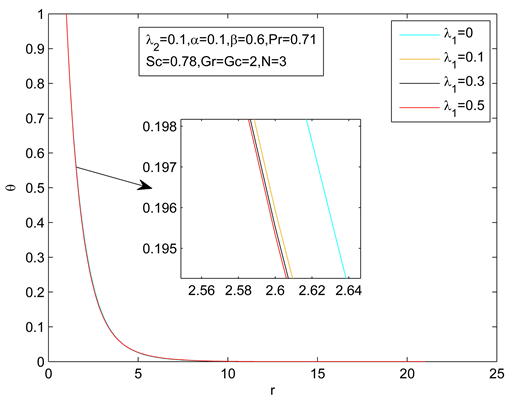
Figure 11. Temperature distribution for different λ₁

图11. 不同λ₁下的温度分布

Figure 12. Temperature distribution for different λ₂

图12. 不同λ₂下的温度分布

离散化并进行求解。离散化的过程中，应用隐式的Crank-Nicolson格式和L1-算法得到控制方程的差分格式，把非线性的耦合的偏微分方程转化为了一个线性的方程组。结果表明，部分参数对速度有很大的影响，但是对温度和浓度的影响并不大。a的值越小，速度曲线的波峰越高。 $\alpha ,{\lambda }_1,{\lambda }_2$ 对温度、浓度几乎没有影响。b对速度的影响与a对速度的影响非常的相似。b对温度和浓度的影响的规律不是很明显。

Figure 13. Concentration distribution for different λ₂

图13. 不同λ₂下的浓度分布

Figure 14. Temperature distribution for different λ₂

图14. 不同λ₂下的温度分布

基金项目

The Fundamental Research Funds for the Central Universities (No.FRF-BR-17-004B)。