1. 引言
随着CAD/CAM及数字几何获取技术的发展,大量的复杂形体通过激光采样获取,采样获取的点云数据一般转换为三角网格表示。三角网格模型 [1] 是三维空间中由一系列相互连接的平面三角片组成的一种曲面离散逼近表达形式;三角网格模型后续中的一个重要应用是重构或识别这种由离散的、低级几何表示的三角网格模型为高层次的设计、制造特征,或者分割为有意义的部件;特征识别或者部件分割的一个最基本工作是网格特征边界线的识别和提取。
为此国内外对三角网格模型的特征线识别开展了大量的研究 [2] [3] [4] ,但大多数都是通过计算某些几何特征值,例如曲率,二面角,形状直径等,通过设置阈值和判定规则来判定网格边是否是特征边界。在规则和边界突出的模型中,这些方法有一定的适应性。然而对于扫描获取的点云网格,由于采样模型的粗糙度和洁净程度、采样噪音、数据计算误差等因素,使得点云网格崎岖不平,并且网格十分密集,很难判定某个网格边就是特征边;此外在一些曲面过渡边界也很难用单个或少量几何特征值去判定,判定阈值也难以确定。目前一些学者把机器学习的方法应用到三角模型的分割、特征识别领域 [5] [6] [7] ,基于数据驱动的识别方法可以不依赖于硬的代码规则或显式的编程指令,将人对形状的边界认知融合到分类器中,从而实现更接近实际的特征边界识别结果。
本文深入分析特征边界几何特征,在文献基础 [8] 上开展基于数据驱动和学习的特征边界识别方法的研究,实现采用AdaBoost算法的基于学习的特征边界边识别方法。该算法在三角网格数据模型的基础上省略了对特征点的判断,而是直接判断三角网格模型的三角边是否为特征边,提高了效率,识别结果更接近实际边界。
2. 特征边的几何特征分析
2.1. 特征边界线
特征通常是指三维模型上有特定工程意义的形状。根据模型处理的工程意义,有可能需要识别设计特征、制造特征或者是分析特征。图1给出一个简单的通过激光扫描获取的齿轮零件的三角网格模型,图1(a)是该模型渲染效果图,图1(b)是该模型线框图。从图1可以看出,特征边界线一般发生在表面几何变化处,有些几何表面发生突变,形成锐边,自然很容易识别为边界边,有些区域可能缓慢过渡,但需要分割出不同特征面,例如图1所示的齿轮零件模型,感兴趣的特征包括齿形面、齿根面等,不同的
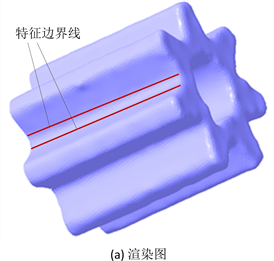
Figure 1. Triangular mesh model and feature boundary line of gear parts
图1. 齿轮零件三角网格模型和特征边界线
特征面之间交线构成特征边界线。因此特征边界线的确定也是与不同的应用相关的。
2.2. 特征边界线的几何特征
2.2.1. 主要几何特征
特征边界线一般是几何表面变化的交线,经过多年的计算机图形学研究和发展,研究和总结了大量关于几何表面的描述特征,主要特征如下:
1) 二面角(Dihedral angle):两个三角形面之间的夹角。在三角网格模型中,通常特征边界边处的二面角都小于平坦处的二面角,即二面角小于某一给定阈值的边可能是边界边,反之,则不是。
2) 曲率(Curvature):曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,它表明了曲线偏离直线的程度,曲率是几何体不平坦程度的一种衡量。在三维欧氏空间中的曲线和曲面的曲率有平均曲率、主曲率和高斯曲率三个基本要素。
平均曲率:是空间上曲面上某一点任意两个相互垂直的正交曲率的平均值。如果一组相互垂直的正交曲率可表示为K1,K2,那么平均曲率则为:K = (K1 +K2 )/2。
主曲率:过曲面上某个点上具有无穷个正交曲率,其中存在一条曲线使得该曲线的曲率为极大,这个曲率为极大值Kmax,垂直于极大曲率面的曲率为极小值Kmin。这两个曲率属性为主曲率。它们代表着法曲率的极值。
高斯曲率:两个主曲率的乘积Kmax×Kmin,即为高斯曲率,又称总曲率,反映某点上总的完全程度。
由曲面论可知,在三角网格模型中,特征边界边处边界边顶点的曲率较大,因此需要计算边界边顶点或者附近顶点的曲率。
曲率计算离不开曲面拟合,本文中采用二阶邻域曲面拟合法。曲率估计算法在文献 [9] [10] 的基础上,经过比较采用Taubin曲率估计算法,得到最大曲率K1和最小曲率k2。计算得到反应曲面弯曲程度的高斯曲率KG、描述一个曲面嵌入周围空间的平均曲率Km、描述一个体素周围体积的局部解剖学形状的形状指数(Shape Index)SI和反映曲面凹凸程度的曲度(Curvedness) CV。
3) 形状直径:SDF [11] 定义在三维模型表面每个点上的一个实值函数,它反映了网格表面上每个面到网格对面的距离。在三角网格模型中,特征边界边处边界边顶点的形状直径较大。
三维模型可以看作是由多个二维网格表面围成具有一定体积的特定空间,SDF就是定义在这些网格表面的标量函数,它将三维模型的体积信息映射到其包围的二维网格表面上,以实现对三维模型形状特征的数值描述。本文给定射线精度 ,张角
,张角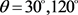 计算得到形状直径函数(SDF) [12] 。
计算得到形状直径函数(SDF) [12] 。
2.2.2. 特征边界线识别问题
前面已经介绍,特征边界线与应用或者是语义相关,有领域知识的人可以感受模型的几何特征的变化,结合识别的需求,确定特征边界线。
在三角网格模型中,复杂的几何表面被离散为小的三角面片,通常三角面片的边是局部几何变化集中处,因此本文选择三角形一条边作为分析和处理单元,特征边界的边都是由一组三角形边组成。这样,特征边界线识别问题可以转化为三角面边的二元分类问题,即如果是边界,则分类值为1,否则为−1。
3. 基于学习的特征边界识别
3.1. 识别方法的总体方案
根据上述特征边界线分析,采用传统的单一几何特征和阈值方法很难准确识别实际所需要的特征边界。本文提出基于学习的特征边界识别方法,识别的总体方案如图2所示。
从图2可以看出,基于学习的特征边界识别方法由如下两部分组成:
1) 特征边界识别学习模型
基于学习的识别方法的中心点是将特征边界识别形式化为一个边界的分类问题。首先收集一批相同工程意义的零件网格模型,并且通过人工识别标记需要识别的边界,分类模型通过对已标记的网格模型进行学习训练,学习就是通过输入一组训练数据集产生一个分类函数。训练数据集由一组正确标记网格边计算得到的几何特征向量,分类器选择AdaBoost,AdaBoost是一种迭代算法,其核心思想是针对同一个训练集训练不同的分类器(弱分类器),然后把这些弱分类器集合起来,构成一个更强的最终分类器(强分类器)。
2) 特征边界识别模型
训练好的边界识别模型就可以作为识别模型,去识别实际中需要识别网格模型。当然,开始识别的结果还比较粗糙,需要对边界不断细化。本文不作详细介绍,重点论述学习模型。
3.2. 几何特征向量
由前面特征边的几何分析,可以选择一组几何特征值来刻画特征边界,这组组几何特征值形成特征边的几何特征向量。几何特征值数量直接影响后续学习和识别的效率,选择哪些几何特征值,选择多少来构造几何特征向量是基于学习的特征边界识别的关键之一。根据前面分析,本文提出如下17项几何特征构成学习和识别的几何特征向量:
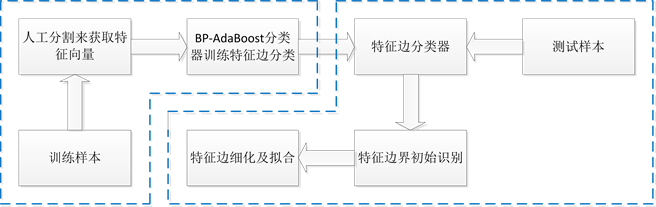
Figure 2. Learning-Based feature boundary recognition scheme
图2. 基于学习的特征边界识别方案
1) 二面角
两面角是最能反映一条三角边的凹凸特性,尖锐边界基本上由二面角一个几何特征就可以确定。很多文献把20度定为边界特征的阈值,二面角如果大于20度,则该边就是一条特征边。因此将二面角选为几何特征向量的第一个几何特征,设为x1。
2) 曲率
前面已经介绍,曲率是几何体不平坦程度的一种衡量,通常指一个几何区域。影响边的凹凸变化,显然在边的左右邻域区域曲率的变化有很重要的影响,如图3所示。因此三角边左右两侧顶点或相邻顶点的曲率可以作为几何特征向量。本文将计算边e1左侧顶点v1的曲率,包括两个主曲率Kmax,Kmin,一个平均曲率K,一个高斯曲率,形状因子和曲率度,分别构成e1的特征向量的x2,x3,x4,x5,x6,x7;同时计算边e1右侧顶点v2的曲率,包括相同的6个值,分别构成e1特征向量的x8,x9,x10,x11,x12,x13。
3) 形状直径和全局曲率
分别计算边两侧顶点形状直径和全局曲率,构成特征向量的x14,x15,x16,x17。
3.3. 学习训练数据
训练数据就是一组标记的边的几何特征向量值和分类结果。训练数据可以表达为如下形式:
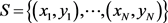
式中每一个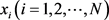 代表一条边的17维特征向量,yi代表该条边的标记的分类结果,
代表一条边的17维特征向量,yi代表该条边的标记的分类结果, ,如果是特征边,即为1,否则为−1。
,如果是特征边,即为1,否则为−1。
显然,要获得一个复杂三角网格体的特征边的训练数据是困难的,为此本文采用Visual C++2010和OpenGL开发了一个训练数据手工标记工具,如图4所示。该手工标记工具完成如下工作:
1) 读入STL或其他格式的网格模型文件;
2) 系统内构建一个基于面的网格拓扑模型,将STL网格文件读入后,系统重构网格顶点、边和三角面之间的拓扑关系,从而可以高效地查询各个网格元素。
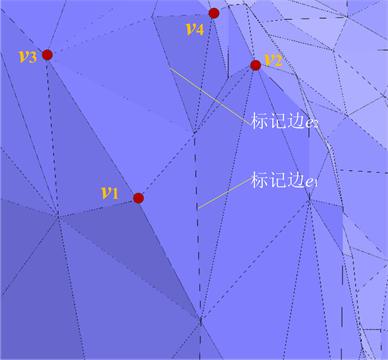
Figure 3. Feature edge geometric feature vector selection
图3. 特征边几何特征向量选择
Figure 4. Manual marking window for training data
图4. 训练数据手工标记窗口
3) 采用OpenGL技术实现了一个对网格模型标记的交互工具,例如边鼠标选择和自动捕捉、模型缩放和旋转、模型渲染和边界绘制等。
4) 对标记选择边自动计算出上述17个特征值的特征向量,能将训练数据保存输出在一个关系表中。
3.4. 基于BP-AdaBoost分类器的特征边识别
对一组特征向量进行学习训练后获得分类能力是机器学习最普遍的功能。目前国内外提出各种类型的分类器,例如支持向量机分类器SVM等。本文所需要的特征边界识别分类器的主要思想是要求对输入的一组特征向量,其分类输出结果与标记的结果误差最小,在不断地迭代中获得各个特征对分类影响的权重。
经过比较和测试,BP-AdaBoost分类器有更好的性能,其主要特点是将多个弱分类器组合成一个强分类器,能在迭代中自动选择和增强合适的特征使得分类误差最小,取得更好的分类效果。本文选择BP-AdaBoost分类器 [13] [14] 作为特征边界识别分类器,BP-AdaBoost分类器配置如图5所示。
3.4.1. BP-AdaBoost分类器学习
BP-AdaBoost分类器学习包括如下四个步骤:
1) 数据选择和网络初始化
从上述标记网格的边几何特征向量数据集选择训练数据,设选择m组数据,初始化测试数据的分布权值Di(i) = 1/m。BP神经网络作为弱分类器,它的结构由样本的输入特征值的维数以及输出维数确定。隐藏层的数量以及每层神经元的数量可以通过试验和误差决定,如果隐藏层包含太多的神经元会导致数据的过适应,这样会降低神经网络的通用性。反之如果隐藏层包含的神经元数量太少,则会导致神经网络较低的学习效率。
2) 弱分类器(BP网络节点)训练
在训练数据训练第t个BP网络时,预测训练数据输出,得到预测序列g(t)的预测误差和et,计算公式如下:
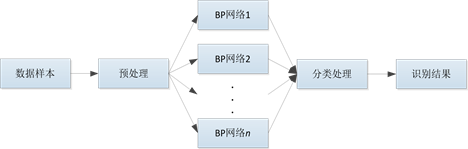
Figure 5. BP-AdaBoost classifier model
图5. BP-AdaBoost分类器模型
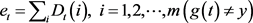 (1)
(1)
上式中g(t)为预测结果,y为标记结果。
3) 计算预测弱分类器序列权重,并根据测试数据进行权重调整
根据预测序列g(t)的预测误差et计算序列权重wt,权重计算公式为:
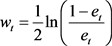 (2)
(2)
4) 组合得到强分类函数
训练T轮后就得到T组BP分类函数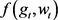 ,将各组弱分类BP函数组合得到强分类函数h(x),分类函数如下:
,将各组弱分类BP函数组合得到强分类函数h(x),分类函数如下:
 (3)
(3)
3.4.2. 基于训练的BP-AdaBoost分类器特征边界识别
在上述分类器学习基础上,就可以用于特征边的识别。其识别过程如图6所示。主要有如下步骤:
1) 网格预处理。首先将要识别的网格模型输入进行预处理,将所有两面角小于10度(10度为特征边最低阈值,可以修改)的三角边过滤,没有必要参与识别,大大减少了识别的数据量。
2) 几何特征向量计算。对参与识别三角边,按照上述方法计算该边的17维特征向量,获得一组由边标识的特征向量组。
3) 将边标识的特征向量组输入训练后的分类器,获得是否是特征边分类结果。
4) 连接相邻分类为特征边的三角边形成特征边段,最后对分类特征边段细化、连接和样条拟合,输出识别的特征边界。
4. 识别实验
本文采用的网格模型、网格特征标记工具及几何特征向量计算等通过Visual C++ 2008和OpenGL开发平台编程实现,BP-AdaBoost分类器采用Matlab实现数据训练和特征边识别。
就上述方法,本文开展了初步的识别实验。从图1所示齿轮零件中选择标记端面轮廓边线、齿面特征边等5组边进行标注,每组边包含120至380条三角形边,还随机选择100条非特征边(两面角大于10度),计算出2000多个训练数据集。输入到了BP-AdaBoost分类器进行训练。训练后的模型再对该齿轮零件进行特征边识别,识别结果基本符合预期。
从识别结果看,基于学习的方法识别判定不仅只依赖于单一阈值,更重要的是识别结果与人的知识认知接近,因此更符合实际需要的识别结果。
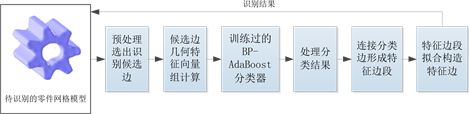
Figure 6. The identification process of feature boundary based on classifier
图6. 基于分类器的特征边界识别过程
5. 结束语
本文在对数字采样网格模型特征边界的几何特征分析基础上,开展了基于学习的三角网格模型的特征边识别方法的研究,将特征边识别形式化为三角边的二元分类问题,提出和总结标识特征边几何特性的17维特征向量;通过手工对三角边的标记,获取特征边分类学习训练的数据集;通过对BP-AdaBoost分类器大量数据进行训练,使得BP-AdaBoost分类器具备特征边界识别的能力。开展了初步的识别实验,获得基本符合预期的结果,特别适合于通过采样获取的,含有大量噪声的模型的识别。
该项工作还只是一个对方法初步的尝试,实验模型和数据还偏少,下一步将对更多模型数据进行识别实验。此外,通过分类器识别还只是特征边界识别的初步结果,后续还有大量工作,例如边界细化和拟合等工作。
基金项目
国家自然科学基金项目(51775081, 51375069)。