基于BP神经网络的物镜畸变改正模型精度探讨

The Discussion on the Precision of Lens Distortion Model Based on BP Neural Networks

摘要: 非量测数码相机的检校是近景摄影测量研究的热点问题。本文基于标准图像和畸变图像，采用BP神经网络建立物镜畸变改正模型，针对普通数码相机图像的像点坐标进行改正，并与传统Brown多项式畸变模型的结果进行对比分析。实验结果表明，BP神经网络改正模型的精度要优于传统多项式物理模型的精度，能够较好地满足高精度的近景摄影测量需要。

Abstract: Non-metric digital camera calibration has become a research hotspot in the field of close-range photogrammetry. Based on the standard image and distorted image, this paper has corrected the point coordinates of the non-metric digital camera image by using BP neural network to establish the model of objective lens distortion correction, and the point coordinates were compared with the points corrected based on traditional polynomial distortion models proposed by Mr Brown. The result showed that the accuracy of BP neural network model would be higher and could meet the requirement of the close-range photogrammetry of high precision.

1. 引言

近景摄影测量作为摄影测量学的一个重要分支，目前已经广泛应用于各类测绘生产实践。随着非量测数码相机的不断发展，使得近景摄影测量日趋数字化、自动化。然而，普通数码相机并不是专门为量测而设计生产的，尽管其具有价格低廉、携带方便、可随意调焦等优势，但非量测数码相机存在着较大的物镜畸变 [1] ，必须经过可靠性检校才能达到近景摄影测量的相应精度需求 [2] 。

传统的物镜畸变校正模型主要是把畸变类型分为径向畸变和偏心畸变 [3] 等，基于共线方程及其改化式建立相应的物理模型，以求取相关的畸变参数 [4] 。但是这类物理模型通常计算复杂，且一般只能满足中低精度的要求，在实际的高精度近景摄影测量生产实践中，必须要考虑完整的光学畸变模型 [5] ，甚至包括电学畸变和机械畸变等 [6] 。

采用BP神经网络算法来训练拟合物镜畸变函数，是将整个物镜畸变看成是一个整体，利用畸变图像与非畸变图像之间的某种映射关系来完成相机的高精度检校 [7] 。该方法不仅简单易于实现，且能较全面的拟合畸变函数 [8] 。本文基于BP神经网络的物镜畸变改正模型对像点坐标进行校正，通过不断的学习训练来优化模型的权值和阈值，以得到最优解。相较于传统Brown模型的物镜畸变模型而言，无需建立复杂的物理表达式。最后基于两种物镜畸变模型对畸变图像进行了像点坐标的校正实验，并通过实验结果论证了BP神经网络模型精度的可靠性。

2. 非量测相机物镜畸变改正原理

2.1. BP神经网络物镜畸变改正模型

非量测数码相机检校的目的是恢复每张影像光束的正确形状，以保证摄影中心、像点、物点位于一条直线上。针对非量测数码相机，需要检校的内容主要有内方位元素(包括像主点坐标x₀、y₀及像主距f)和畸变差(△x，△y)。其中，物镜畸变是影响非量测数码相机精度的关键因素。畸变差通常指光学畸变差，是由物镜系统设计、制作和装配所引起的像点偏离其理想位置的点位误差，光学畸变差是影响像点坐标质量的一项重要误差源 [1] 。

采用BP神经网络算法对像点进行校正，是将物镜畸变差看成是一个整体。BP神经网络是由非线性变换单元组成的多层前馈神经网络，也可被称为误差反向传播网络 [9] 。一般分为输入层、隐藏层、输出层。本文所采用的BP神经网络拓扑结构如图1所示：

基于BP神经网络的畸变映射函数关系表达式为：

$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=f\left({\displaystyle \underset{i=1}{\overset{m}{\sum }}{w}_i\left[\begin{array}{l}{x}_i\\ y_i\end{array}\right]-\theta }\right)$ (1)

其中： $x_i$ 、 $y_i$ 为畸变图像的标志点坐标，作为网络训练输入值； $x^{\prime }$ 、 $y^{\prime }$ 为标准图像中的对应标志点坐标，作为网络目标输出值； $w_i$ 是权系数，q为阈值。

BP神经网络可以实现从输入到输出之间的任意非线性映射关系的训练拟合，在调整权阈值的过程中常采用的训练方法有LM算法、动量BP算法、可变学习速率BP算法、弹性BP算法、拟牛顿法、最速梯度下降法等 [10] 。在训练过程中，通过不断地调整网络权值和阈值，使得经过网络多次迭代后的输出值与目标值的最小均方误差逐渐达到最小，并将最终的权值和阈值分配在BP神经网络模型之中，得出最优畸变改正函数模型。

2.2. Brown物镜畸变改正模型

根据摄影测量原理 [11] ，考虑物镜畸变差，非量测数码相机的像点坐标可表示为：

$\begin{array}{l}{x}^{″}=\Delta x+x\\ y^{″}=\Delta y+y\end{array}$ (2)

其中， $\left(\Delta x,\Delta y\right)$ 为像点畸变差； $\left(x,y\right)$ 为像点坐标的量测值； $\left(x^{″},y^{″}\right)$ 为像点物镜畸变改正值。

Brown物镜畸变改正模型是根据几何光学的原理，将物镜畸变差分为径向畸变和偏心畸变以及CCD面阵内变形等 [12] 。基于Brown模型的畸变差表达式如式(3)：

$\begin{array}{l}\Delta x=x_{\Delta }\left(r^2{K}_1+r^4{K}_2+r^6{K}_3\right)+\left(r^2+2x_{\Delta }^2\right)P_1+2x_{\Delta }{y}_{\Delta }{P}_2+x_{\Delta }{B}_1+y_{\Delta }{B}_2\\ \Delta y=y_{\Delta }\left(r^2{K}_1+r^4{K}_2+r^6{K}_3\right)+\left(r^2+2y_{\Delta }^2\right)P_2+2x_{\Delta }{y}_{\Delta }{P}_1\end{array}$ (3)

3. 实验及结果分析

选取一组对应的标准图像和畸变图像，分别对两图像进行灰度化和二值化处理，图像分辨率均为2368 × 4208，如图2(a)、2(b)所示：

在图2中的畸变图像和标准图像中分别选取对应的56个标志点坐标作为训练集，8个未参与训练的标志点坐标作为畸变改正模型检测集。BP神经网络隐层神经元为10个，隐藏层传递函数为正切曲线函数tansig，输出层传递函数为线性函数pureline。量测相关标志点的坐标形成数据文件，由于隐层sigmoid

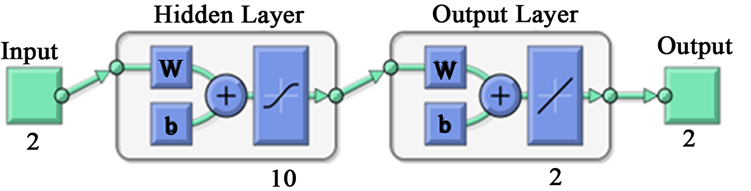
Figure 1. BP neural network topology of the image

图1. BP神经网络拓扑结构图

(a) (b)

Figure 2. (a) Distorted image; (b) standard image

图2. (a) 畸变图像；(b) 标准图像

函数的敏感性，需对数据进行归一化处理 [13] 。本实验中，采用收敛速度快且精度较高的LM算法进行网络训练。

BP神经网络的训练集坐标取自图2畸变图像和标准图像中一一对应的56个标志点坐标，其中，训练样本占70%，测试样本15%，检验样本15%，均为随机产生；有效性检查次数设为6，网络的初始权值在［-0.5，0.5］之间随机给出，误差性能函数取最小均方误差MSE。当训练结束时，物镜畸变函数形式便已确立，相应的权值和阈值也就贮存在了BP神经网络之中。

通过对比多次训练拟合的结果，从中选出BP神经网络的一种最优模型，对应的训练曲线如图3所示。

图3中，Train代表训练样本学习曲线，Test代表测试样本学习曲线，Best代表当前模型最小均方误差，Validation表示模型第303次迭代时，有效性检查次数达到了预设值6，停止训练。运用该模型对未参与训练的8组检测点像点坐标进行仿真处理，并与相应的实际像点坐标真值对比。结果如表1所示。

为验证BP神经网络函数模型的精度，以Brown畸变改正模型为对比，采用56个像点坐标建立关于7个畸变参数的超定方程组，解算出7个畸变参数，再代入未参与训练的8组检测点对应的像点坐标值，求出对应像点的畸变改正值，并与实际像点坐标值对比分析误差，测试结果如表2所示。

综合表1、表2结果，分别计算模型中误差可知，BP神经网络畸变改正模型精度为0.00139；传统Brown模型精度为0.03143。BP神经网络畸变改正模型精度相对较优，能更好的满足高精度近景摄影测量的需求。

4. 结束语

本文的BP算法对待定点校正误差在0.004~0.0001之间，相比传统Brown多项式模型误差0.06~0.001之间要低出很多。实验结果表明，采用BP神经网络可以更全面的拟合出畸变函数，能较好的满足近景摄影测量高精度的相关需求。但BP神经网络模型也存在不足，其解可能为局部最优而不是全局最优，如何快速准确地在多个局部最优解中选择出全局最优解需进行多次试算确定。此外，本文针对桶形畸变图像进行的训练，得出的畸变函数模型不能适用于枕形畸变等其他畸变类型，对于不同的畸变图像均需重新对其进行学习训练。

Figure 3. BP neural network training curve

图3. BP神经网络学习曲线

Table 1. Results of BP neural network simulation experiment

表1. BP网络仿真实验结果

Table 2. Results of the brown model experiment

表2. Brown模型实验结果

基金项目

公路地质灾变预警空间信息技术湖南省工程实验室科研项目(kfj150602)。