1. 引言
社会网络分析(Social Network Analysis, SNA)是从嵌入社会情境中个体的“关系”角度出发，揭示群体结构及其与心理与行为的相互作用(马绍奇，焦璨，张敏强，2011)。社会网络数据由一组行动者和行动者之间的社会关系组成，这种数据的独特性引起了越来越多的学者开始将SNA应用于心理学的研究。近年来，国内有关SNA方法在心理学方面的研究文章逐渐增多。例如，通过社会网络分析的方法探讨了同伴团体对青少年问题行为的影响(侯珂，邹泓，刘艳，金灿灿，蒋索，2014)，个性特征与社会网络的关系及其本土化发展的趋势(李永强，黄姚，2014)。通过社会网络的视角探讨了个体情绪智力与任务绩效的关系(张辉华，2014)，以及中学生的班级友谊关系网络(唐文清，钟阳，张敏强，叶素静，刘晶，黄兆峰，2014)。
但是在SNA中，缺失数据是一个重要且无法回避的难题之一。SNA的数据是反映个体之间联系的关系数据，所以和社会科学的其他领域相比，SNA中的缺失数据问题更为复杂。已有研究表明，SNA的缺失数据原因主要包括边界规范问题，固定选择的研究设计和网络调查中的无应答(Kossinets, 2006)。边界规范问题是网络研究中指定行动者或者关系之间包含的规则(Laumann, Marsden, & Prensky, 1983)。固定选择的研究设计指网络中行动者和关系的缺失依赖于研究设计中提名选择的限定(Holland & Leinhardt, 1973)。网络调查中的无应答包括应答者完全缺失和特定项目的数据缺失(Stork & Richards, 1992; Rumsey, 1993)。其中，网络调查中的无应答是社会网络调查中最经常出现的缺失情况。对于无应答情况，通常采用插补法进行处理。
在实际应用中，研究者经常会选择简单的插补方法对缺失数据进行处理，如均值插补，热卡插补等单一插补法。在SNA中，均值插补包括条件均值插补和非条件均值插补。条件均值插补是通过部分观察网络的网络特征如度数，或者通过条件分布中的预测值来取代缺失数据。非条件均值插补是用网络的密度，行动者的平均入度关系(行动者接收的关系)均值和行动者的平均出度关系(行动者发出的关系)均值来代替缺失数据(Gabbay & Zuckerman, 1998)。均值插补能够得到无偏的均值估计，但是容易低估方差和协方差。热卡插补是指通过同一个数据集中的应答行动者数据的估计分布中，抽取插补值替代无应答行动者的缺失数据(Sande, 1982)。这种方法能避免由于插补造成扭曲的变量分布，但是容易高估方差。总体而言，单一插补法会离散数据的分布以及网络中行动者之间的关系，即使在完全随机的缺失机制下，也容易产生有偏差的估计值(Huisman, 2014)。因此，在单一插补法的基础上，多重插补法和重建法逐渐发展起来。
不同的缺失数据原因和缺失数据处理方法，还涉及一个重要的问题，数据是否系统缺失。如果数据是系统缺失，那么缺失概率是否和观察变量(性质或属性)有关(黄菲菲，张敏强，2016)。Rubin (1976)根据缺失引起的偏差程度定义了三种类型的缺失数据：完全随机缺失(Missing Complete At Random, MCAR)，随机缺失(Missing At Random, MAR)和非随机缺失(Missing Not At Random, MNAR)。因此，在使用不同的缺失数据处理方法时，还应考虑数据的缺失机制。
相比于国外研究，国内尚无对SNA中缺失数据的插补处理方法进行对比研究。本研究希望通过程序的编写，将重建法与多重插补法相比较，进一步探讨在不同缺失机制情况下，两种方法对SNA中缺失数据处理的准确性和可靠性。
2. 缺失数据处理方法
2.1. 多重插补法
Rubin (1987)提出多重插补法。多重插补法指的是通过插补值的预测分布中通过一组m > 1的合理插补值替代每一个缺失值的过程。m个插补集间的差异性反映了缺失数据可从观察数据进行推断的不确定性(庞新生，2012)。用多重插补法对数据处理后，就会有m个完整的数据集，每一个数据集都可以用分析完整数据的方法进行分析。在对每一个数据集分析后，就可以将结果(估计值和标准误)合并，用Rubin或者其他学者提出的简单方法得到能够反映缺失数据不确定性的整体估计值和标准误(如图1所示)。
在社会网络分析中，多重插补法同样分三步对缺失数据进行处理：第一步是数据插补。通过插补模型为每个缺失行动者或者缺失关系产生m (m > 1)个合理插补值，得到m组完整数据集。插补过程根据变量类型及数据缺失模式的不同而有所不同。针对类别数据，Schafer (2010)年提出多项式模型和对数线性模型，该类模型可以考虑类别变量间的任意关系。但变量数较多时需要大样本量才能拟合模型(Royston, 2004; Finch, 2010; Schafer & Olsen, 1998)。此外，logistic回归模型和鉴别函数(discriminant function)目前被广泛使用，SAS的PROC MI、R软件的MICE软件包等将其设置为类别数据的插补模型。关于m的取值，Rubin (1987)认为3~5个插值即可。
第二步是运用标准统计分析方法分析每一个完整数据集。每个参数得到m个估计值和对应的标准误。
第三步是将m组结果进行整合并得到最终参数估计值，然后进行统计推断。整合过程一般使用Rubin (1987)法则。假设m个完整数据集获得的参数估计值为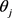
，对应的标准误为
，则最终的参数估计值为：
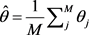
最终标准误的估计值为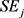
均值及m个估计值的组间差异之和的开方：
和单一插补法相比，多重插补法得到的有效统计推断值考虑了由缺失数据引起的不确定性，但唯一的缺点是处理过程较为复杂。
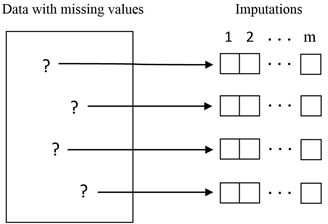
Figure 1. Multivariable matrix with missing data and multiple interpolation method
图1. 有缺失数据的多变量矩阵及多重插补法
2.2. 重建法
Stork和Richards (1992)通过网络中行动者之间的互惠关系对缺失数据进行推断首先提出了重建法。他们认为，重建法从本质上而言是用一个行动者已接受到的关系去进行测量，因此在分析过程中并没有增加新的关系。使用重建法时，值得注意的一点是，应答行动者和无应答行动者之间的应答模式不仅要具有相似性且二者之间的关系必须是有效的，即使用重建法处理SNA中的缺失数据时必须满足相似性和可靠性两个原则。已有研究发现，重建法能够有效的重建网络中行动中缺失的大部分关系，并且在构建完整网络时不会出现不收敛的问题，所以不少学者将重建法作为处理社会网络缺失数据的常用方法(Gabbay & Zuckerman, 1998; Huisman & Steglich, 2008)。
重建法根据社会网络的类型主要分为两种程序：1) 针对无向网络而言，重建法通过观察到的行动者之间或者部分应答者和无应答者之间的关系重构网络(Stork & Richards, 1992)。2) 针对有向网络而言，所有行动者的缺失关系Xij可以通过二元关系中对应行动者的观察数据进行替代：Xmisij = Xji，即通过应答行动者来插补对应关系的观察值(Huisman, 2014)。
和多重插补法相比，重建法的处理过程较为简单，并且能够最大化地利用有效信息去构建社会网络(黄菲菲，张敏强，2016)。但是，重建法无法构建两个无应答行动者之间的缺失数据。
3. 研究方法
3.1. 数据生成
本研究选择关于班级SNA及其对学业拖延影响机制研究中的一个学业咨询网络子样本，是由40名初一学生及他们之间的有向关系组成的班级网络数据。这个网络数据采用提名生成法，要求行动者写出在学习上遇到困难或疑问时会请教班上的哪些同学。行动者属性包括自我监控行为，采用Snyder编制的《自我监控量表》。该问卷共25个项目，采用2级(是/否)记分，反向记分项目有11题。问卷总分越高，表示自我监控水平越高。
和边界规范问题及固定选项的研究设计这两种缺失数据原因相比，无应答是社会网络调查中最经常出现的缺失情况，所以本次模拟研究的缺失数据原因定义为行动者无应答。
3.2. 模拟程序
根据设定的模型和条件，运用Monte Carlo模拟方法模拟含有缺失数据的SNA分析数据并使用两种方法对缺失数据进行处理，数据模拟次数为500。数据模拟的过程分为以下四个步骤：第一步，产生完整的网络数据。第二步，设置缺失数据，缺失率为0.05。在R软件的simFrame软件包生成不同缺失机制的缺失数据(MCAR：分别在关系数据上根据缺失率随机设置缺失；MAR：随机缺失概率和行动者的自我监控分数相关；MNAR：非随机缺失概率和网络特征，行动者入度值相关)。第三步，缺失数据处理及SNA，其中，重建法在R中自编，多重插补法在R中的MICE软件包进行数据插补。第四步，计算第一步的完整网络数据和第三步用两种方法处理缺失数据的网络数据的统计指标。本研究采用中心势(网络的整体中心度)计指标，具体公式如下所示：
(1)
3.3. 比较标准
参考相关模拟研究，本研究选择偏差(Bias)和误差均方根(RMSE)作为统计指标的评价指标。Bias用来衡量估计量出现偏差的方向性，RMSE用来衡量估计量精确性和稳定性。Bias和RMSE的评价标准是值越小，说明参数估计值越接近真值，估计越准确，反之则差(Lee & Dodd, 2012; 罗幼喜，田茂再，2010)。具体公式如下所示：
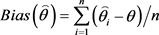(2)
(3)
4. 结果
上文已述，两种方法进行比较的第一步是生成完整的网络数据。从图2中，我们可以看到整个班级的学业咨询网络密度很高。另外，从连线整体形状来看，属于闭合图形，说明班级中不存在可能被孤立的个体，因此这是一个完整网络。
对于相同的500批模拟数据，分别计算不同缺失机制情况下完整网络的中心势和两种方法处理后的网络中心势估计值的偏差Bias值和误差均方根RMSE值，结果如表1所示。
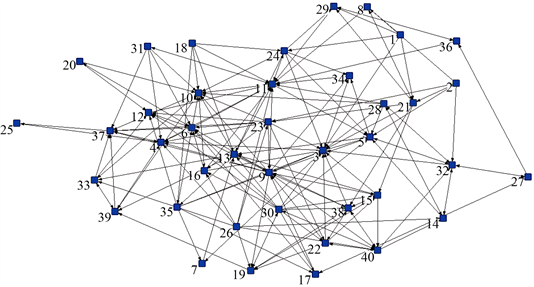
Figure 2. Class academic consulting network graph
图2. 班级学业咨询网络社群图
Table 1. Bias and RMSE estimation of reconstruction method and multiple imputation method
表1. 重建法和多重插补法估计的Bias和RMSE
5. 结论与讨论
从表1可知，在MCAR和MNAR情况下，重建法对中心势的估计出现了正值偏差，而多重插补法对中心势的估计为负值偏差。两种方法对中心势估计值的均值偏差都较小，这说明两种方法对社会网络中缺失数据的处理具有较高的准确性。另外，在误差均方根的比较上，多重插补法均比重建法低，总体看来多重插补法对社会网络中缺失数据的处理具有较高的可靠性。在MAR情况下，重建法对中心势的估计出现了正值偏差，多重插补法则出现了无偏估计，说明与重建法相比，多重插补法对社会网络中缺失数据的处理具有更高的准确性。在误差均方根的比较上，两种方法对中心势估计的差异值为3.14，这说明多重插补法对社会网络中缺失数据的处理具有较高的可靠性。
总体来说，在三种不同的缺失机制下，重建法和多重插补法对缺失数据处理的准确性大致相当，而多重插补法对缺失数据的处理具有更高的可靠性，造成这一现象的原因可能和重建法无法构建两个无应答行动者之间的缺失数据有关，这使得重建法无法正确地定义网络的结构。
然而重建法和多重插补法在其它缺失情况下的比较研究值得我们去探索，例如，本研究仅在小样本量和小缺失率的情况下比较了两种方法的表现，并没有对样本量和缺失率水平的变化进行设定。因此，重建法和多重插补法在不同缺失条件下的比较研究也将会成为以后研究的一个重要方向。另外，本研究的统计指标限定在中心势，但已有研究发现，SNA中不同统计指标的稳健性在遇到缺失数据的情况下是有差异的(Smith & Moody, 2013)，所以研究者可以继续从事这个方向的研究，探讨重建法和多重插补法在不同社会网络统计指标计算下的比较研究。
基金项目
本论文得到嘉应学院人文社会科学研究项目资助(编号：2017SZY01)。