1. 引言
在图像产生的过程中,因为受到某些因素的干扰,使得图像质量退化,上述图像即为模糊图像 [1] [2] [3] [4] 。模糊图像被广泛应用于各种领域中,一个典型的例子就是电子监控系统。随着城市建设的不断发展,很多公共场所及企业均安装了电子监控 [5] - [10] 。然而,当出现状况后,监控数据的回放通常存在数据不完整,画面不清晰的情况,导致关键信息由于模糊而无法辨认 [11] [12] [13] 。因此,对于模糊图像特征识别的研究具有非常重要的意义,已经成为相关学者研究的重点课题,受到了广泛的关注。在对模糊图像特征进行识别的过程中,出现图像模糊成因及相关参数未知的现象,导致传统的基于不变矩的模糊图像特征识别过程,由于忽略了模糊相关参数的选择,处理模糊图像时很难采集到有效的匹配点 [14] [15] [16] 。
本文首先分析了传统模糊图像特征识别方法的原理和弊端,提出一种改进的模糊图像特征识别方法,同时通过实验验证了该方法的有效性。
2. 基于不变矩的模糊图像特征识别原理及弊端分析
不变矩特征即图像中具有平移、旋转及比例不变性的数学特征。不变矩方法主要通过采集模糊图像中具有平移、旋转及比例不变性的数学特征实现模糊图像特征的识别。
由于模糊图像特征针对平移、旋转及比例变换均具有不变性,因此,需通过普通矩与中心矩的线性组合获取。
通过归一化的二阶和三阶中心矩组合获取七个对平移、旋转及尺度变换不变的矩。该矩针对平移、旋转和大小比例变化均为不变的。
基于不变矩的模糊图像特征识别方法,忽略了模糊相关参数的选择,处理模糊图像时很难采集到有效的匹配点,不能适应模糊图像的实时变化及不确定性,无法有效实现模糊图像特征识别。
3. 基于SIFT匹配的模糊图像特征识别方法
3.1. 模糊图像预处理
通常情况下,受外界环境的干扰,模糊图像会存在明显的噪声干扰,需对其进行平滑处理。在对模糊图像进行预处理的过程中,本文设定一个方差阈值,如果待识别图像的方差超过该阈值,则对其进行平滑预处理,否则,无需对其进行预处理。
用 描述原始模糊灰度图像,引入时间变量t,对下述偏微分方差进行计算,获取一组逐渐平滑模糊图像
描述原始模糊灰度图像,引入时间变量t,对下述偏微分方差进行计算,获取一组逐渐平滑模糊图像 :
:
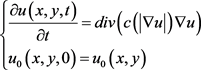 (1)
(1)
式中,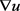 用于描述模糊图像梯度模;扩散系数
用于描述模糊图像梯度模;扩散系数 为关于
为关于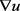 的非负函数,同时有
的非负函数,同时有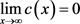 ,其又被称作边界处停止函数,主要负责调控扩散速度,保持边界。理想情况下,扩散系数需使各向异性扩散在灰度变化平缓的范围内快速完成,在灰度波动较大的位置,也就是模糊图像特征处,低速扩散甚至不扩散。本文给出两个扩散系数:
,其又被称作边界处停止函数,主要负责调控扩散速度,保持边界。理想情况下,扩散系数需使各向异性扩散在灰度变化平缓的范围内快速完成,在灰度波动较大的位置,也就是模糊图像特征处,低速扩散甚至不扩散。本文给出两个扩散系数:
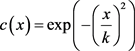 (2)
(2)
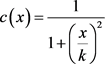 (3)
(3)
为了对式(1)进行求解,首先需对其进行离散化处理,则有:
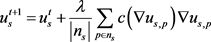 (4)
(4)
式中, ;t用于描述迭代次数;λ用于描述分布系数权值,
;t用于描述迭代次数;λ用于描述分布系数权值,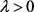 ;
;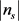 用于描述相邻点的数量;依据
用于描述相邻点的数量;依据 性质分析式(4)可以看出:如果像素s在灰度变换范围内,
性质分析式(4)可以看出:如果像素s在灰度变换范围内,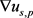 一定趋近于0,则
一定趋近于0,则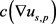 趋近于最大值1,扩散较快,从而使
趋近于最大值1,扩散较快,从而使 向其邻域像素
向其邻域像素 的灰度值靠近,也就是对s进行了一次平滑处理;如果s与p之间有模糊图像边缘,则梯度
的灰度值靠近,也就是对s进行了一次平滑处理;如果s与p之间有模糊图像边缘,则梯度 值将很大,当前
值将很大,当前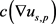 趋近于0,扩散效率低,则
趋近于0,扩散效率低,则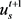 基本不受
基本不受 的影响,保持了s与p之间的边缘。
的影响,保持了s与p之间的边缘。
3.2. 模糊空间的构建
若直接采用清晰图像与模糊图像进行匹配,则最终得到的匹配效果通常达不到令人满意的效果。尽管采用上述方法对模糊图像进行预处理,匹配效果仍旧不佳。因此,本文引入模糊空间思想。模糊空间主要包括高斯模糊子空间、光照模糊子空间与运动模糊子空间。上述三个模糊子空间是通过同一张清晰图像依据各种模糊运算产生的,本文以高斯模糊子空间的产生为例,分析模糊子空间的产生过程。
高斯模糊子空间是清晰图像经高斯平滑处理后产生的。针对高斯平滑函数参数的选择无特殊要求,能够达到图像从清晰到逐渐模糊的效果即可。本文采用模板尺寸是7,尺度(方差)渐渐增加的二维高斯函数对该类模糊图像进行处理:
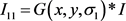 (5)
(5)
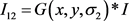 (6)
(6)

 (7)
(7)
其中,I用于描述清晰图像, 用于描述经一定尺度平滑后的模糊图像,
用于描述经一定尺度平滑后的模糊图像,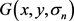 用于描述一定尺度的高斯平滑函数。通过改变高斯函数的尺度参数σ形成一系列的模糊图像
用于描述一定尺度的高斯平滑函数。通过改变高斯函数的尺度参数σ形成一系列的模糊图像 ,其组成了清晰图像I的模糊空间中的高斯模糊子空间。
,其组成了清晰图像I的模糊空间中的高斯模糊子空间。
光照模糊子空间与运动模糊子空间的产生过程和高斯模糊子空间相似,只是对原清晰图像进行的模糊运算不一样。
3.3. SIFT特征提取和匹配
进行完上述两步之后,本文采用SIFT算法将经预处理后的模糊图像依次与建立的模糊空间中的图像进行匹配,从而实现模糊图像特征识别。SIFT特征提取和匹配的实现主要包括三部分:SIFT特征点检测、SIFT特征描述符的生成及SIFT特征匹配。
3.3.1. SIFT特征点检测
SIFT特征点检测首先需塑造模糊图像的多尺度空间和高斯金字塔图像;然后令相邻尺度的2个高斯图像作差,获取高斯差分多尺度空间(Difference-of-Gaussian, DoG);于DoG尺度空间中获取局部极值点,再利用曲面拟合法对上述极值点进行进一步定位,同时通过高斯差分图像的海森矩阵对初始特征点中边缘点和对比度较低的点进行删除,从而获取模糊图像特征点。SIFT特征采集的详细过程如下:
1) 检测尺度空间极值。将模糊图像的尺度空间描述成一个函数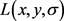 ,该函数可通过可变尺度高斯函数
,该函数可通过可变尺度高斯函数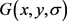 和输入模糊图像
和输入模糊图像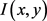 卷积获取:
卷积获取:
 (8)
(8)
式中,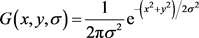 。
。
高斯差分尺度空间 可描述成存在常数乘性尺度因子k的相邻尺度高斯函数的差分和原始图像的卷积,得到上述高斯差分模糊图像中的局部极值,即可获取尺度空间域中的图像特征点,
可描述成存在常数乘性尺度因子k的相邻尺度高斯函数的差分和原始图像的卷积,得到上述高斯差分模糊图像中的局部极值,即可获取尺度空间域中的图像特征点, 可描述成:
可描述成:
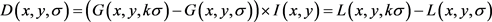 (9)
(9)
2) 准确定位特征点。首先确定候选特征点处的拟合函数:
 (10)
(10)
求导获取 和相应的极值
和相应的极值 ;逐渐对X进行调整,求解最优点,删除
;逐渐对X进行调整,求解最优点,删除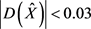 的弱特征点,并且得到候选特征点的准确位置、尺度。
的弱特征点,并且得到候选特征点的准确位置、尺度。
删除边缘点时得到特征点的Hessian矩阵,用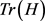 、
、 描述其特征值的和及乘积,用γ描述
描述其特征值的和及乘积,用γ描述
矩阵特征值的比,为了检测主曲率是否低于阈值γ,需判断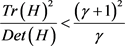 是否成立,γ通常取6~10。
是否成立,γ通常取6~10。
3.3.2. SIFT特征描述符的生成
生成SIFT特征描述符主要是为了确定特征点的主方向,为特征点匹配提供依据。获取主方向后,在进行匹配的过程中,可将模糊图像旋转至主方向,从而使模糊图像保持旋转不变性。(x, y)处的梯度值及方向可分别描述成:
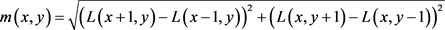 (11)
(11)
 (12)
(12)
在以特征点为中心的邻域窗口中进行采用,同时依据梯度方向直方图对邻域像素的梯度方向进行统计,与直方图最高峰值点相应的方向就是主方向。
以特征点为中心选择8 × 8的窗口,再在4 × 4图像中求出8个方向的梯度方向直方图,构建各梯度方向的累加值,产生一个种子点。一个特征点可通过4 × 4,也就是l6个种子点进行描述,一个种子点存在8个方向向量信息,因此,一个特征点可形成4 × 4 × 8共128个数据,也就是形成128维SIFT特征向量或特征描述符。
3.3.3. SIFT特征匹配
获取特征向量后,通过欧氏距离对两个向量的相似度进行度量,公式描述如下:
 (13)
(13)
为了降低计算过程中的复杂度,将特征点较少的模糊图像作为参考图像,针对参考图像A中的某特征点a和待匹配模糊图像B中全部特征点,求出其欧氏距离,按照距离升序完成对模糊图像B中特征点的排序,将距离较小的前1%点和点a进行进一步的SIFT特征匹配。
SIFT特征匹配依据最近邻比值法,通过 BBF(Best Bin First)获取最近邻与次近邻,若最近邻距离和次近邻距离之比未超过某阈值th,则最近邻点和该特征是最佳匹配对;反之,认为其为冗余点,公式描述如下:
 (14)
(14)
4. 仿真实验分析
为了验证本文提出的基于SIFT匹配的模糊图像特征识别方法的有效性,需要进行相关的实验分析。实验采用的模糊图像内容相对复杂,同时模糊图像受视角、光照强度、尺度不同等因素的干扰,通过匹配率与误匹配率对本文方法和传统基于不变矩的模糊图像特征识别方法的性能进行评价。实验平台如下:CPU Intel P4 2.4 GHz,内存 512 MB,Windows XP SP3,Visual C++ 6.0。
进行多次反复实验,求出其匹配率、误匹配率和匹配时间的对比结果,如表1所示。
分析表1可以看出,在图像分别存在尺度变化、光照变化及旋转的条件下,本文方法能够有效的保持高匹配精确度,也就是高识别精度,同时所需时间大大降低,完全能够满足实时性较高的系统,验证了本文方法的有效性。
图1描述的是采用本文方法得到的模糊图像特征匹配识别结果。

Figure 1. Method matching results in this paper
图1. 本文方法匹配结果

Table 1. Comparison of two methods of recognition performance
表1. 两种方法识别性能比较
分析图1可以看出,本文方法能够有效的对模糊图像特征进行匹配,从而完成模糊图像特征的识别。这是因为本文方法首先对模糊图像进行预处理,使模糊图像更加平滑,SIFT方法将大部分局部结构相似的特征排除,能够通过全局特征补偿因视角变换造成的局部信息的缺失,使匹配数量增多。
5. 结论
本文提出一种基于SIFT匹配的模糊图像特征识别方法,分析了传统方法的弊端,对模糊图像进行预处理,引入模糊空间思想,模拟各种图像模糊成因对数据库图像集进行扩建。采用SIFT算法将经预处理后的模糊图像依次与建立的模糊空间中的图像进行匹配,获取模糊图像特征点,生成SIFT特征描述符,确定特征点的主方向,将模糊图像旋转至主方向,使模糊图像保持旋转不变性。利用欧氏距离对两个向量的相似度进行度量,通过判断最近邻距离和次近邻距离之比是否超过某阈值,确定最近邻点和该特征是否为最佳匹配对,从而实现模糊图像特征识别。仿真实验结果表明,所提方法具有较高的识别精度。
基金项目
1) 河南省科技厅科技发展计划科技攻关项目(立项编号:172102210428)
2) 河南省科技厅科技发展计划科技攻关项目(立项编号:182102310040)
3) 平顶山学院青年科研基金项目(立项编号:PXY-QNJJ-2018005)