1. 引言
为研究素数密度和素数分布,作者曾在中文杂志《前沿科学》2016年第2期发表论文《素数分布研究的一种新思路》 [1] ,核心方法是用埃氏(Eratosthenes)筛法对素数生成过程进行建模与递推。依埃氏筛法,为生成不超过正整数n的全部素数,以素数序列
,在不含1的正整数列
初始背景中,由2,3依次到
实施筛法。文献 [1] 规范了埃氏筛法的三步骤操作规则:1) 后续p筛在前面p0筛除剩余中进行无公倍数的纯净筛除,除第一个被筛除数p2外,对p0筛
余周期内全部筛余数的筛除率和对其中任一筛余数的筛除概率均为
,避免了因素数之间公倍数引
起的重复筛除,简称“纯净筛除”。2)
筛剩余(简称p筛剩余)形成以
为起点,以
为周期的移位周期重构,简称“周期重构”。3) p筛以概率1固定筛除p2点,从而截取p0筛剩余周期
之首
,确认区间
的生成素数,简称“筛余截首”。
基于步骤1),步骤2),论文证明了
筛除剩余在其周期
内平均密度
(1.1)
式中,c为欧拉常数,e为自然对数的底。
逻辑的结论是:n邻域素数平均密度D必定在
基础上,由“筛余截首”决定。“筛余截首”以概率1固定筛除p2而不是以概率
筛除p2,p2点的筛除概率比其它点增加了
,由此必然减小筛余周期前端密度,使区间
内素数平均密度低于
筛除剩余周期内剩余数的平均密度。
为讨论“筛余截首”对素数密度的影响,正整数m的密度分布成为必须直面的问题,首先对此进行概念研究。
2. 正整数在自然数列中的密度分布
定义2.1 (正整数在自然数列中的密度分布):正整数m在自然数列
中,m存在或被删除对m邻域和
全域密度影响程度在
全部元素上的分配函数
(n为自变量,m为参变量),称m在
上的密度分布函数。正整数m在自然数列
中的密度分布函数是以n为自变量,以m为参变量的伽玛(Gama)函数
(2.1)
对应的累积密度函数是
(2.2)
称对
在其主要作用域上对应的均匀分布函数为正整数m在自然数列中的等效均匀密度分布。
定义说明:
满足以下基本要求
1) m的密度函数
在
全域上的总和
(2.3)
与概率密度函数同形异义。
2) m为
均值与密度最大值,对应于概率密度函数的数学期望和众值,邻域在概率密度函数中应起主要作用。
应为一个以m为均值和最大值的双向平滑的曲线,向0方向应以较快速率下降并交于0点,向+¥方向应以较快速率下降并一直拖尾到+¥,因此,
应符合伽玛分布。
伽玛分布的一般表达式为 [2]
(2.4)
对应的积累密度函数为
(2.5)
使n满足众数的充要条件是
,即
解得
,设
时满足众数条件,即
(2.6)
同时应为
的均值,即
(2.7)
将(2.6) (2.7)联立,解得
将此结果代入(2.4)即得(2.1),代入(2.5)即得(2.2)。
3) 随着m的加大,
应逐步逼近以m为中心、左右对称的正态分布,但向+¥方向的无限拖尾永远不会消失,
永不等同正态分布。因此,
在区间
的累级分布
应逐步趋于0.5−,在区间
的累级分布
应逐步趋于0.5+。
是自然数全域上的函数,与正整数及其累积即阶乘密切相关,这个定义反映了邻域与全域的关系。
猜想2.2:全体正整数的密度分布对同一自然数的总和为1,记作
(2.8)
由此使数轴上全体正整数布满时,数轴上任何位置的密度为1,删去某一正整数对数轴上任何位置密度均有影响,但影响的分布服从被删去正整数的密度分布,全体正整数被删去后,数轴上任何位置密度均为0。由此建立数轴上正整数密度分布的加性运算规则,表为
(2.9)
式中,n为任意选择的一个自然数,m为全体正整数。
设想此猜想可通过对式(2.1)的函数分析证明。
推论2.3 (正整数在自然数列中的等效均匀密度分布命题):
正整数m在自然数列
中的等效均匀密度分布函数表为以n为自变量,以m为参变量的函数
(2.10)
式中
为m密度分布的等效作用域,k为位于区间
(2.11)
的确定常数,数的性质和具体值待进一步研究仿真确定,本文称k为素数常数。
证明:先分析等效均匀分布的前提条件。
时,伽玛分布无限趋近但永不等同左右完全对称的正态分布,
时具有与 不同的拖尾效应。m点是相应伽玛分布的众数点和均值点,因此,
不同的拖尾效应。m点是相应伽玛分布的众数点和均值点,因此,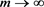
时,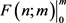 将无限趋近但不会等于
将无限趋近但不会等于 ,差别主要在拖尾部分。所以
,差别主要在拖尾部分。所以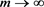 时,必然存在常数k满足
时,必然存在常数k满足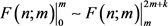 ,且拖尾积累密度
,且拖尾积累密度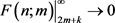 。正整数的等效均匀分布以此为前提。
。正整数的等效均匀分布以此为前提。
1) 由于 时伽玛分布趋向左右对称的正态分布,k应是个小常数;2) 对密度敏感的是小素数,但大素数与小素数对渐近趋势的影响是一致的;3) k的选择要兼顾参变量m左右积累密度差距小和截尾影响小这一相互矛盾的因素(
时伽玛分布趋向左右对称的正态分布,k应是个小常数;2) 对密度敏感的是小素数,但大素数与小素数对渐近趋势的影响是一致的;3) k的选择要兼顾参变量m左右积累密度差距小和截尾影响小这一相互矛盾的因素(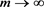 时趋同)。
时趋同)。
为更有针对性,对m为小素数平方数的几种情况(任意情况趋势相同),令 ,
, ,计算结果如表1。
,计算结果如表1。
计算仿真表明:k由小变大时,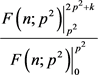 由小变大,而
由小变大,而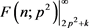 则由大变小,取
则由大变小,取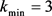 或
或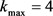 能较好兼顾要求:满足在区间
能较好兼顾要求:满足在区间 的积累密度与区间
的积累密度与区间 积累密度无限接近,即
积累密度无限接近,即 ,亦即
,亦即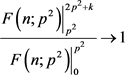 ,且拖尾积累密度
,且拖尾积累密度 。
。

Table 1. Part of the gamma cumulative distribution calculation results
表1. 伽玛累积分布部分计算结果
已可看出 的基本趋势,即一定存在常数k
的基本趋势,即一定存在常数k

满足要求。 时,满足其在区间
时,满足其在区间 的积累密度与区间
的积累密度与区间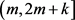 积累密度无限接近,即
积累密度无限接近,即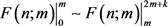 ,且拖尾积累密度
,且拖尾积累密度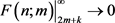 。
。
忽略拖尾积累密度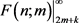 ,将m的伽玛密度分布看作在区间
,将m的伽玛密度分布看作在区间 的均匀分布,并称
的均匀分布,并称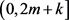 为均匀分布的等效作用域,m在自然数列
为均匀分布的等效作用域,m在自然数列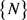 中的等效均匀密度分布函数可表为
中的等效均匀密度分布函数可表为
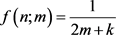
推论2.3证毕。
在一定条件下,正整数的伽玛密度分布函数可用等效均匀分布来等效。
3. 素数平均密度
猜想3.1 (素数平均密度):n邻域素数平均密度
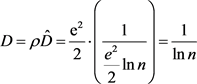 (3.1)
(3.1)
式中, 称素数特征数,是一个由自然常数和欧拉常数表示的数。
称素数特征数,是一个由自然常数和欧拉常数表示的数。
式(3.1) n小时D不准确;n较大时D比较准确;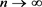 时D趋于精确。
时D趋于精确。
证明:文献 [1] 已证明, 筛除剩余在其周期
筛除剩余在其周期 内平均密度
内平均密度
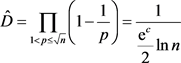 (3.2)
(3.2)
当n很大时( )可等效表为
)可等效表为
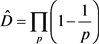 (3.3)
(3.3)
式中p表示全部素数。
分析“筛余截首”作用。“筛余截首”是在p0筛除剩余周期前端以概率1固定筛除相邻素数p2,由此确认 区间的素数。这必将降低p0筛余周期前端的密度。由正整数密度的加性运算规则,不失一般性,可用降密因子
区间的素数。这必将降低p0筛余周期前端的密度。由正整数密度的加性运算规则,不失一般性,可用降密因子 表示。
表示。
对以概率1固定筛除p2,其中概率 已在表示p筛降密作用的式(3.3)
已在表示p筛降密作用的式(3.3) 中考虑,因此,λ应修正为
中考虑,因此,λ应修正为 。
。
由式(2.1),p2的密度分布函数是以n为自变量,以p2为参变量的伽玛函数
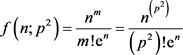 (3.4)
(3.4)
考虑到:1) p相邻素数间平均间隔为 ,故p2邻域素数间平均间隔为
,故p2邻域素数间平均间隔为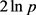 ,
,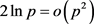 ,即在间隔很大的被删除相邻p2之间,存在很多素数,被筛除的p2点相对于保留下的素数点是“稀疏”的。2) 相邻被筛素数平方数可分别表为p2和
,即在间隔很大的被删除相邻p2之间,存在很多素数,被筛除的p2点相对于保留下的素数点是“稀疏”的。2) 相邻被筛素数平方数可分别表为p2和 ,p2的密度分布函数的根均方差为
,p2的密度分布函数的根均方差为 ,且
,且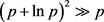 ,即
,即 远在
远在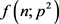 的方差之外,即被筛素数平方数远在相邻密度曲线的方差之外。3) 相邻伽玛密度函数的中心逐步移位和相似性。4) 被筛素数平方数p2在筛除剩余数中随机分布。
的方差之外,即被筛素数平方数远在相邻密度曲线的方差之外。3) 相邻伽玛密度函数的中心逐步移位和相似性。4) 被筛素数平方数p2在筛除剩余数中随机分布。
由此使相邻被删除p2的伽玛密度分布函数适用于等效均匀分布,引式(2.10),可用 对应的均匀分布来等效。即
对应的均匀分布来等效。即
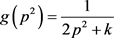 (3.5)
(3.5)
再将这一降密作用嵌入到表示p筛降密作用的式(3.3)中,随之一起递推,形成加性降密因子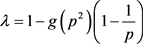 之间的乘性递推。由此实现小素数降密因子向大素数的逐步传递,并形成素数平均密度
之间的乘性递推。由此实现小素数降密因子向大素数的逐步传递,并形成素数平均密度

等效表为
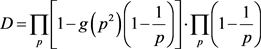 (3.6)
(3.6)
令素数特征数
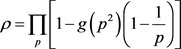 (3.7)
(3.7)
即
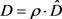
由此得
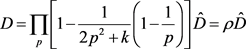 (3.8)
(3.8)
相应地
 (3.9)
(3.9)
引式(2.11)

式(3.8)对应表为
 (3.10)
(3.10)
对ρ判敛,取

随p增大,序列 单调递减且有下界1,
单调递减且有下界1,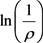 收敛于一个大于0的常数,因此,ρ必收敛于一个小于1的常数。
收敛于一个大于0的常数,因此,ρ必收敛于一个小于1的常数。
实际上,相邻p2的等效作用域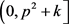 相互自嵌套并不断扩大,由此在累乘中形成降密因子的后向传递,并通过累乘形成极限。
相互自嵌套并不断扩大,由此在累乘中形成降密因子的后向传递,并通过累乘形成极限。
当n很大时,对 ,式(3.10)等效表为
,式(3.10)等效表为
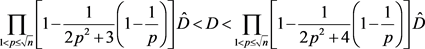 (3.11)
(3.11)
即

仿真到 表明,
表明,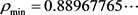 ,
,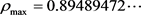 ,
,
即
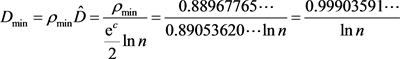 (3.12)
(3.12)
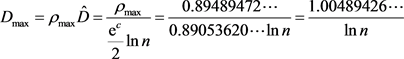 (3.13)
(3.13)
由此确定当 和
和 时,D的以
时,D的以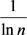 为中心的非常接近的下限和上限
为中心的非常接近的下限和上限
 (3.14)
(3.14)
对 ,通过
,通过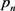 “筛余截首”,确认区间
“筛余截首”,确认区间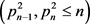 的素数,猜想存在合适的满足式(2.10)
的素数,猜想存在合适的满足式(2.10) 的
的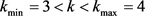 ,同时满足
,同时满足 ,由此使n邻域素数密度
,由此使n邻域素数密度 成立。
成立。
猜想3.1证毕。
需要说明:对由小到大的素数,等效作用域由小变大,相同的常数k对伽玛分布的截尾效应由大变小,在等效作用域定义下以均匀分布表示伽玛分布的理想程度由小变大,都反应了素数由小变大时粒度由大变小的事实。
 与高斯(Gauss)建议式相同 [3] [4] 。
与高斯(Gauss)建议式相同 [3] [4] 。
D的不准确性源于:在素数特征数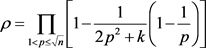 的渐近积累过程中,与
的渐近积累过程中,与 一样,小素数粒度大、积累速率高。ρ与
一样,小素数粒度大、积累速率高。ρ与 相乘后加权因子抵消,但对小素数的不准确性以素数的固有特征保留下来。
相乘后加权因子抵消,但对小素数的不准确性以素数的固有特征保留下来。
正整数在自然数列的密度分布概念及“筛余截首”中正整数p2对筛除剩余周期前端密度的影响,是素数密度成立的关键。正整数的伽玛密度分布和等效均匀分布,以及筛除p2的降密作用,看来都是合理的。核心
的问题,一是正整数在自然数列的伽玛密度分布 概念;二是存在满足
概念;二是存在满足 的常数k,将正整数p2的伽玛密度分布
的常数k,将正整数p2的伽玛密度分布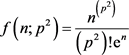 等效表为均匀分布
等效表为均匀分布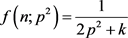 ,常数k能满足在区间
,常数k能满足在区间 与区间
与区间 的积累密度无限接近,即
的积累密度无限接近,即 ,且拖尾积累密度
,且拖尾积累密度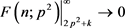 ;三是将这一等效均匀分布通过累乘表示连续筛除p2的降密作用必然满足降密因子
;三是将这一等效均匀分布通过累乘表示连续筛除p2的降密作用必然满足降密因子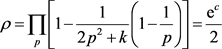 ,式中,
,式中, 为对全部素数的连乘,由此导致n邻域素数密度
为对全部素数的连乘,由此导致n邻域素数密度 。
。
限于作者水平和高精度计算条件,不能对此深入研究。真诚地希望数学界和各界批评指正,开展专题理论研究和高精度仿真计算,完成正整数密度分布的概念研究和猜想的证明。期待数学界的权威论证,向所有提出批评和做出研究的朋友、老师和专家表示衷心感谢。
推论3.2 (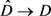 映射关系):由式(3.2)
映射关系):由式(3.2) 及式(3.1)
及式(3.1)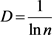 ,可直接建立由
,可直接建立由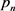 筛除剩余周期
筛除剩余周期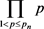 内剩余平均密度
内剩余平均密度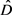 到n邻域素数平均密度D的1-1映射关系 [5]
到n邻域素数平均密度D的1-1映射关系 [5]
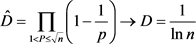 (3.15)
(3.15)
映射式(3.15)就是由线性筛除剩余通往非线性素数的桥梁,它直接源于埃氏筛法的“纯净筛除”、“周期重构”和“筛余截首”三步骤,素数密度直接源于埃氏筛法的素数生成机制。
推论3.3 (筛除剩余周期内前端密度):设有以p0为基础的连续p0筛、p筛和 筛,p筛剩余在周期
筛,p筛剩余在周期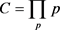 内保持筛除概率
内保持筛除概率 和筛余密度
和筛余密度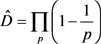 的同时,由于“筛余截首”即p筛以概率1固定筛除p2的积累作用,使p0筛余周期前端
的同时,由于“筛余截首”即p筛以概率1固定筛除p2的积累作用,使p0筛余周期前端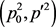 的密度低于周期
的密度低于周期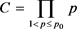 内平均密度,这部分剩余数除p2外全部为素数。筛除p2的有效作用域是
内平均密度,这部分剩余数除p2外全部为素数。筛除p2的有效作用域是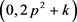 ,而前端
,而前端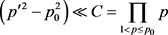 ,
, 固定筛除点在
固定筛除点在 内非常靠近p2的位置。这样,筛除p2在确认
内非常靠近p2的位置。这样,筛除p2在确认 内素数的同时,也为筛除
内素数的同时,也为筛除 确认区间
确认区间 内素数做好了实际准备。
内素数做好了实际准备。
推论3.4 (素数分布的分形结构与混沌性态):埃氏筛法的“纯净筛除”、“周期重构”和“筛余截首”,由简单机制生成了复杂性态。1) 在形成 的过程中,形成周期内平均密度
的过程中,形成周期内平均密度 是线性行为,但
是线性行为,但
由于互质素数的“纯净筛除”和“周期重构”,已经产生了筛除剩余数的轨道不可预测性。2) 随着素数由小到大,“筛余截首”中连续p2筛除的自相似的有效作用域形成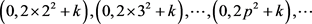 无限自嵌套,并通过等效均匀分布的降密累乘,使素数密度和筛除剩余密度之比快速收敛到
无限自嵌套,并通过等效均匀分布的降密累乘,使素数密度和筛除剩余密度之比快速收敛到
 ,其间线性筛除剩余的周期由小依阶乘率变大,这代表了素数快速走向混沌的过程。
,其间线性筛除剩余的周期由小依阶乘率变大,这代表了素数快速走向混沌的过程。
不过,由于 空间无限,这种混沌永远不会形成由混沌常数表征的倍周期分岔。3) 这就决定了,能用代数式给出表达的,除个别情况外,只能是素数的统计特性,包括密度、数量,以及对素数序列和初始正整数生成背景加不同约束条件的素数组的数量。一般而言,不方便以代数式对素数的轨道特性和结果进行确切描述。
空间无限,这种混沌永远不会形成由混沌常数表征的倍周期分岔。3) 这就决定了,能用代数式给出表达的,除个别情况外,只能是素数的统计特性,包括密度、数量,以及对素数序列和初始正整数生成背景加不同约束条件的素数组的数量。一般而言,不方便以代数式对素数的轨道特性和结果进行确切描述。
4. 由素数密度到素数分布经典问题
文献 [1] 证明了p筛对p0筛除剩余的筛除率和p筛对p0筛除剩余中各剩余数的筛除概率均为 ,记为
,记为
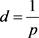 (4.1)
(4.1)
文献 [1] 为确定不超过正整数x的素数数量,将素数密度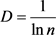 进行由代表最小素数的正整数2到最大正整数x的积分
进行由代表最小素数的正整数2到最大正整数x的积分 ,并将积分展开为渐近级数
,并将积分展开为渐近级数
 (4.2)
(4.2)
式中r为渐近级数的最佳截断
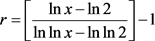 (4.3)
(4.3)
从而得出了与素数定理一致的更加精细的表示。
借助筛除概率式(4.1)、素数密度式(3.1)、 映射式(3.15)和渐近级数概念,对包括孪生素数猜想和哥德巴赫猜想在内的各类约束素数组,如孪生素数猜想、多孪生素数猜想、偶数哥德巴赫猜想、素数差哥德巴赫猜想、
映射式(3.15)和渐近级数概念,对包括孪生素数猜想和哥德巴赫猜想在内的各类约束素数组,如孪生素数猜想、多孪生素数猜想、偶数哥德巴赫猜想、素数差哥德巴赫猜想、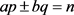 哥德巴赫猜想等,可将相应约束条件嵌入埃氏筛法的递推步骤,通过素数组生成背景分析和筛除作用分析,在埃氏筛法对筛除剩余数的筛除率的基础上,确定对筛除剩余数组的筛除率,进而借助简单的数学变换和
哥德巴赫猜想等,可将相应约束条件嵌入埃氏筛法的递推步骤,通过素数组生成背景分析和筛除作用分析,在埃氏筛法对筛除剩余数的筛除率的基础上,确定对筛除剩余数组的筛除率,进而借助简单的数学变换和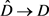 映射关系确定约束素数组密度和数量,并以相应不同形式对数积分的渐近级数表示。
映射关系确定约束素数组密度和数量,并以相应不同形式对数积分的渐近级数表示。
作者在中文杂志《前沿科学》2016年第4期发表的论文《素数分布研究新思路的若干应用》 [5] 中,研究了这些问题并得出了结论,多数结论与历史上已形成的猜想一致。这说明各类素数分布问题均可纳入基于素数生成与筛除剩余分布演化机制的统一理论框架,也印证了作者通过建模与递推,解析埃氏筛法,研究素数分布的信念 [1] :1) 机制决定性质,素数分布的性质与特点必然植根于埃氏筛法这个“素数生成系统”中。2) 不能静态的就素数论素数,而要从源头上解析埃氏筛法,在动态中考察素数的生成与演化。3) 必须“庖公解牛”,“于关节处切割自然” [6] ,对素数生成过程和步骤进行客观的准确的切割。4) 各类素数分布问题的基础机制相同,必然存在内在的同一性,因此要整体地综合地相关地而不是孤立地研究这些问题。
致谢
青年高级工程师王炜华博士、汤宏伟、王远和李军博士完成了初稿英译和仿真计算,崔雁巍完成了文档整理和校对,在此表示衷心感谢。衷心感谢爱妻邢纪荣和家人的理解、支持和关爱。