1. 引言
对于非线性奇摄动二阶方程的Dirichlet边值问题 [1] :
其中 为小参数,f是充分光滑函数。近几年来,俄罗斯学派Vasil’eva、Butuzov等用边界层函数法 [2] [3] [4] [5] 研究了该退化方程
具有重根时解的存在性和有效性,国内学者倪明康等研究了一类具有代数衰减边界层的解的性态 [5] ,Songlin Chen等更进一步研究了退化方程具有三重根时的情形 [6] 。本文受其启发,研究如下带有Neumann边值条件的二阶奇摄动方程:
为小参数,f是充分光滑函数。近几年来,俄罗斯学派Vasil’eva、Butuzov等用边界层函数法 [2] [3] [4] [5] 研究了该退化方程
具有重根时解的存在性和有效性,国内学者倪明康等研究了一类具有代数衰减边界层的解的性态 [5] ,Songlin Chen等更进一步研究了退化方程具有三重根时的情形 [6] 。本文受其启发,研究如下带有Neumann边值条件的二阶奇摄动方程:
(1)
(2)
首先给出如下假设:
[H1] 假设函数
,且
关于其变量充分光滑.
[H2] 假设函数
有如下形式:
(3)
且
(4)
表达式(3)可知退化方程有二重根
,为了简化计算,不妨设
。
[H3] 假设
(5)
2. 外部解的渐近展开
设原问题具有下述的形式外部解
(6)
其中
满足
(7)
将(6)代入(3),(7),
(8)
比较上式两边
的同次幂系数
其中
为逐次已知的函数,由上式可得到解
:
因此得出形式外部解(6)。将它代入方程(1)中,将其右端在以点
为展开中心进行泰勒级数展开,合并
的同次幂项之后即得
则可得出估计
(9)
其中
3. 边界层校正项
[H4] 假设
(10)
引入多重尺度变量,首先在x=0处附近构造边界层校正项,设为
(11)
则边值问题(1)~(3)的合成渐近解为
(12)
令
满足
(13)
将(11)代入(3),(13)
(14)
由(2),(6),(11),(12)得
(15)
比较
的同次幂,得如下形式的
(16)
考虑到
为边界层函数,所以要求
(17)
比较(14)式两边
的同次幂系数:
(18)
解得
(19)
对于任意的
当
时,首次形式近似
具有幂率衰减的性态
为了得到边界层函数的正确刻画,我们将对上述满足
的方程进行修正。在(18)式的右端添加一个含未知元
的小量修正项,得
(20)
将问题(20)化为一阶方程
(21)
由分离变量法,可以求得
(22)
其中
(22’)
当
时,
,
。此时
(23)
为了后面的估计,定义
由于
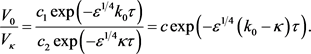
零次近似
满足估计
继续要求
满足:
(24)
解得:
(25)
类似地,我们得出
的方程:
(26)
其中
问题(26)是一个非齐次二阶微分方程,求出其显示解为
这里
(27)
且
满足估计
(28)
类似地,我们还可以得出其余边界层项的估计
(29)
将(11)代入方程(1)中得出估计
(30)
其中

接下来在x = A处附近构造边界层校正项,设为
(31)
则
满足
(32)
对于
,关于
的方程及定解条件为:
(33)
(34)
(35)
其中
是关于
的递归表达式。
特别地
(36)
解得:
(37)
则
有如下指数估计
同问题(30),我们可逐次求出
这里
不难看出,所有的
都有指数估计
将(31)代入方程(1)中,得出估计
(38)
其中
4. 形式解的一致有效性
定理:假设H1~H4成立,那么对于充分小的
,边值问题(1),(2)存在解
,且对于任意的自然数
,有下列关系式成立:
(39)
这里
证明:构造
(40)
我们有
由条件H4,当M充分大时,可得
类似地,构造函数
(41)
可得
则
,
为边值问题(1)的上、下解。
由Nagumo’s定理 [7] 知,边值问题(1)存在解
满足
致谢
感谢审稿老师及编辑老师提出宝贵意见。
基金项目
安徽工业大学研究生创新基金(2017114)。