1. 引言
硼氮纳米管(BNNTs)与碳纳米管(CNTs)由于在结构上类似,因而都具有良好的力学性能。但它们不同之处在于BNNT具有比CNT及更优越的压电特性和机械性能 [1] ,更高的导热性 [2] ,以及更好的抗氧化性 [3] 。另外,与CNT不同,BNNT也具有稳定的半导体性质。BNNT的这种功能使其可以大批量成为纳米级电子和光子器件中的替代材料。因此,BNNT更适合作为一些复合结构的增强材料。随着科学技术的发展,以压电材料做基体和BNNTs做增强材料的新型智能复合材料越来越受到相关研究者和工程界的关注。值得注意的是,这种新型智能复合材料的研究数量有限,其中大部分涉及的是线性问题。因此,对这种结构的非线性行为进行更广泛的研究非常有必要。
自从1991年S. Iijima [4] 制造出了碳纳米管(Carbon nanotubes简称CNTs),由于其新颖的碳原子排列结构和所呈现的各种独特性质,吸引了世界上越来越多的科学工作者开始从事这方面的研究。到1995年,美国Nasreen G. Chopra [5] 等人用等离子体电弧放电法,首次合成了BNNTs。随着科学技术的发展与进步,一些新技术手段被利用在研究中。Zhang [6] 等人通过微积分求积(DQ)逐层建模技术,对多层压电复合板的自由振动进行研究。Yi-ming Fu [7] 等人提出一种非线性模型研究压电弹性层合板的层内和层间界面的破坏效应。Benjeddou [8] 等人用二位封闭式解法,对简支压电夹层板的自由振动问题进行分析。Sladek [9] 等人基于Petrov Galerkin方法,提出了一种无网格的方法,用于功能梯度压电材料性能板弯曲分析。Fu [10] 等人研究了压电功能梯度梁在厚度方向一维稳态导热作用下的热压屈曲、非线性自由振动和动力稳定性。但上述没有研究BNNTs增强压电结构的力学性能。
近来,研究者们对BNNTs增强压电结构的关注越来越高,出现了一些相关研究论文。A. Fereidoon [11] 等人通过分子动学模拟研究了粒径、层数、层间距和温度对氮化硼纳米管的力学性能。Mosallaie Barzoki [12] 等人探究了BNNTs增强内置压电壳的线性屈曲问题。Chen Liu [13] 等人基于非局部理论和基尔霍夫理论,研究了电–热–机械荷载共同作用下压电片的振动问题。Yang [14] 等人探究了电–热–力载作用下BNNTs增强压电圆柱壳的动力响应问题。Kadir Mercan [15] 等人基于Euler-Bernoulli梁理论,提出了一个由弹性基体包围的氮化硼纳米管(BNNT)屈曲行为的简单力学模型。Ghorbanpour Arani [16] 等人研究了硼氮纳米管(BNNTs)嵌入弹性介质中的聚偏氟乙烯(PVDF)复合微电子管,在电热负载下的振动和稳定。基于Eringen的非局部Kirchhoff板理论,A.A. Jandaghian [17] 对在四边简支条件下,功能梯度压电材料(FGPMs)纳米尺度板的自由振动问题研究。
到目前为止,有关BNNTs增强压电板的非线性弯曲研究还未见报道。因此,本文研究电–热–力载下BNNTs增强压电板的非线性静力弯曲问题。空间上采用差分法离散,并给出了不同的力载,电压,温度,体积比等因素对BNNTs增强压电板非线性弯曲的数值计算结果,并进行分析。
2. 基本方程
硼氮纳米管(BNNTs)增强压电板的结构如图1所示,其宽度为b,长度为a,厚度为h,密度为
。坐标系o-xyz位于板的中面(
)处,对压电板施加电压V,升高温度
,及横向荷载
。
2.1. 应变位移关系
假设在x、y、z方向上板任意点的位移用
、
、
表示,用u、v、w表示其中面的相应位移分量,则压电板的位移分量可写为:
(1)
下标(,)表示变量坐标的偏导数。
板非线性应变–位移关系可表示为:
(2)
其中
表示中位面应变分量,
表示中位面曲率和扭率,并且:
(3)
2.2. 本构方程
压电板在机械荷载、热荷载和电荷载共同作用下的本构关系可表示为 [12] [15] :
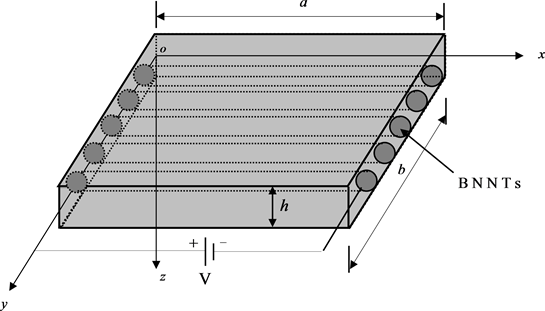
Figure 1. Geometry of piezoelectric plate reinforced with BNNTs
图1. BNNT增强的压电板的几何示意图
(4)
(5)
其中
、
和
分别表示电场、热膨胀系数和温升,而
、
、
分别表示为材料的压电常数、介电常数、弹性常数。这些常数值与材料的结构有关。
一般硼氮纳米管(BNNTs)有扶手椅形状和Z字形两种对称结构,而本文采用Z字形。智能压电板由基体材料为PVDF和增强材料为BNNTs两种材料组成,结构整体的材料常数可以用“XY (或YX) [18] 矩形模型”来计算得到。其表示如下:
(6)
其中:
(7)
上标
和
分别表示复合材料的增强和基体组分。
是基体中增强BNNTs所占的体积比。
2.3. 控制方程
对于用BNNTs增强的压电板,总势能
可以写成:
(8)
其中
和
分别表示应变能和横向载荷所做的功。
应变能表示为:
(9)
考虑方程(4)和(5)以及这里采用的BNNTs的Z字形结构,使得
。因此,等式(9)变成:
(10)
(9)式和(10)式中的
表示体积。
设施加在两端的电压为
则
(11)
横向荷载
所做的功为
(12)
应用变分原理(
),可推导出硼氮纳米管(BNNT)增强压电板的非线性控制方程为:
(13)
其中:
(14)
式中:
(15)
在上面的等式中,
和
是拉伸和弯曲刚度,它们可以定义为:
(16)
引入以下无量纲参数:
(17)
则在电–热–机械载荷下,BNNTs增强板的非线性控制方程为:
(18)
假设板四边简支,则无量纲边界条件分别为:
(19)
3. 求解方法
为了求解满足边界条件(19)的微分方程(18),将无量纲位移函数
、
和
在空间域中离散,以获得其近似解。在空间上采用差分法离散,对于线性项目的处理,以
为例:
(20)
参考差分格式,可以很容易地求得控制方程中其余各线性项各阶偏导数的差分表达式。而非线性项则采用迭代法,在迭代步任一
步中,定解条件和控制方程中的非线性项被线性化,形式如下:
(21)
式中,前两次迭代的平均值为
,而初始迭代步,可以用二次外推求解,如:
(22)
对于不同的迭代步,系数
,
和
取值分别如下:
(23)
对于三次非线性项的处理方法与二次非线性项的处理方法相同。
经过差分法和迭代法线性处理,非线性微分控制方程由最初的偏微分方程组转化成差分格式的线性方程组,然后联立求解。在迭代计算过程中精度为相邻两次计算结果的误差小于10−12。
4. 数值结果和讨论
在下面算例中,探讨了电–热–力载下BNNTs增强压电板的非线性弯曲分析。其几何尺寸为
,
,边界条件为四边简支,压电板增强材料为BNNT,基体材料为PVDF,材料常数如表1所示。横向载荷取为:
(24)
式中,
为外激励幅值。

Table 1. Material constants of PVDF and BNNT
表1. PVDF和BNNT的材料常数
图2(a)和图2(b)表示在体积分数
、电压
、温升 时,几何非线性对BNNT增强压电板弯曲的影响。
时,几何非线性对BNNT增强压电板弯曲的影响。

 (a) (b)
(a) (b)
Figure 2. Effect of geometric nonlinearity on the bending of piezoelectric plate reinforced with BNNTs. (a) Deflection of each point along x; (b) Bending moment of each point along x
图2. 几何线性与非线性对BNNTs增强压电板弯曲的影响。(a) 板沿x方向挠度;(b) 板沿x方向弯矩
从图2可以看出,线性情况下板的无量纲挠度和弯矩大于非线性情况下板的无量纲挠度和弯矩。当横向载荷Q增大时,这种现象更为明显。由于线性情况是基于有限的弹性变形,且在考虑非线性情况下忽略几何关系中的高阶项,因此从某种意义上可以得出线性情况低估了结构的刚度。为了更准确地反映BNNTs增强压电板的性能,非线性效应是必须考虑的。
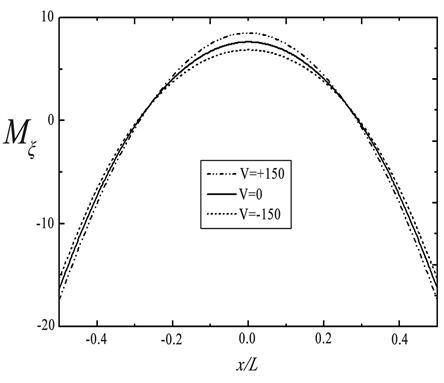
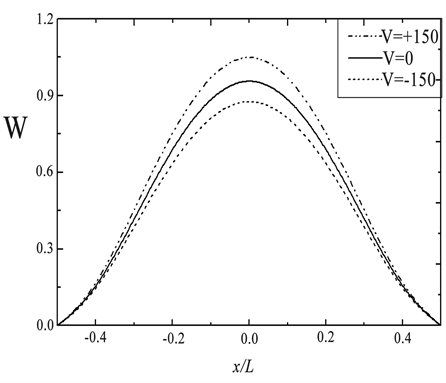
图3显示了在体积分数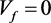 、温升
、温升 、机械载荷为
、机械载荷为 时,正负电压对BNNTs增强压电板非线性弯曲的影响。从图中可以看出,向BNNTs增强压电板施加负电压会减小挠度和弯矩。这是由于施加负电压使BNNT中沿纵向产生极化并导致其收缩。这使得该板的结构更加紧凑和坚固,相应地增强了结构的刚度。因此,结构的挠度和弯矩会减小。图3还描绘了施加正电压时的挠度和弯矩的结果。正如所期望的那样,挠度和弯矩比正常情况增加,结果可以用上述类似的概念来解释。
时,正负电压对BNNTs增强压电板非线性弯曲的影响。从图中可以看出,向BNNTs增强压电板施加负电压会减小挠度和弯矩。这是由于施加负电压使BNNT中沿纵向产生极化并导致其收缩。这使得该板的结构更加紧凑和坚固,相应地增强了结构的刚度。因此,结构的挠度和弯矩会减小。图3还描绘了施加正电压时的挠度和弯矩的结果。正如所期望的那样,挠度和弯矩比正常情况增加,结果可以用上述类似的概念来解释。
 (a) (b)
(a) (b)
Figure 3. Effect of voltage on the bending of piezoelectric plate reinforced with BNNTs. (a) Deflection of each point along x; (b) Bending moment of each point along x
图3. 电压对BNNTs增强压电板弯曲的影响。(a) 板沿x方向挠度;(b) 板沿x方向弯矩
当其电压 、机械荷载
、机械荷载 、体积分数
、体积分数 时,温度对该板的非线性弯曲的影响如图4所示。从图中可以看出,随着温度升高,该板的挠度和弯矩都随之增加。
时,温度对该板的非线性弯曲的影响如图4所示。从图中可以看出,随着温度升高,该板的挠度和弯矩都随之增加。

 (a) (b)
(a) (b)
Figure 4. Effect of temperature on the bending of piezoelectric plate reinforced with BNNTs. (a) Deflection of each point along x; (b) Bending moment of each point along x
图4. 温度对BNNTs增强压电板弯曲的影响。(a) 板沿x方向挠度;(b) 板沿x方向弯矩
图5讨论了在机械负载 、温升
、温升 、电压
、电压 时,硼氮纳米管所占的体积分数对BNNTs增强压电板非线性弯曲的影响。从图中可以看到,当BNNT在基体中的体积分数(
时,硼氮纳米管所占的体积分数对BNNTs增强压电板非线性弯曲的影响。从图中可以看到,当BNNT在基体中的体积分数( )增加时,其挠度和弯矩减小。这是由于体积分数的增加使结构的刚度增强,因此挠度随之减小。
)增加时,其挠度和弯矩减小。这是由于体积分数的增加使结构的刚度增强,因此挠度随之减小。

 (a) (b)
(a) (b)
Figure 5. Effect of volume ratio on the bending of piezoelectric plate reinforced with BNNTs. (a) Deflection of each point along x; (b) Bending moment of each point along x
图5. 体积比对BNNTs增强压电板弯曲的影响。(a) 板沿x方向挠度;(b) 板沿x方向弯矩
5. 结论
本文研究了在电热–热–力耦合作用下,BNNTs增强的压电板的非线性弯曲。结果表明几何非线性,电压,温度,体积分数等参数对压电板的挠度和弯矩有显着的影响。从本文的工作可以得出如下结论:
1) 在其它条件相同的情况下,板在线性情况下的挠度和弯矩大于非线性,当横向荷载Q增大时,非线性效应增强。
2) 在其它条件相同的情况下,对BNNT施加正负电压会导致挠度和弯矩的增加和减少。
3) 在其它条件相同的情况下,挠度和弯矩随着温度的升高而增大,而随着基体中BNNT体积分数的增加而减小。