k次十二面体–师连通圈网络

K Dodecahedron-Shi Connected Cycles Networks

摘要: 互连网络是超级计算机的重要组成部分，片上互连网络是当前研究的热点课题之一。k次十二面体–师连通圈网络是一类重要的互连网络，是在2010年师海忠提出互联网络的正则图连通圈网络模型的基础上设计的新网络模型。它是将十二面体连通圈网络的每个顶点用三角形代替k次得到的，记为DSCC(k)，它是3正则3连通的平面图，且有许多好的性质。文中提出了关于该网络的一系列猜想，如猜想1：k次十二面体–师连通圈网络是Hamilton图，对猜想1、2、3作了严格的证明。作者还利用图的笛卡尔乘积方法构建了新的笛卡尔乘积互连网络DSCC(k)xK₂和DSCC(k)xC_m，并对其性质进行了研究。

Abstract: An interconnection network is an important part of a supercomputer. On chip interconnection network is one of the hot topics in current research. A class of important interconnection network of the K dodecahedron-Shi connected cycle network is a new network model based on the regular graph connected cycle network model of the internet in 2010. It is obtained by replacing each vertex of a dodecahedron connected cycle network with triangle K times, and it is recorded as DSCC(k). It is a 3-regular and 3-connected plane graph, and has many good properties. In this paper, a series of conjectures about the network are proposed, such as the conjecture 1: K dodecahedron-Shi connected cycle network is a Hamilton graph, and the conjectures 1, 2, and 3 are proved strictly. The author also uses the Descartes product method of graphs to construct a new Descartes product interconnected DSCC(k)xK₂ and DSCC(k)xC_m, and study their properties.

1. 引言

互连网络是超级计算机的重要组成部分，它的性能在某种程度上决定着超级计算机的性能。片上互连网络是当前研究的热点课题之一，互连网络通常被模型化为一个图，图的结点对应处理机，图的边对应处理机间的通信信道。各种已有的互连网络参见 [1] [2] [3] [5] - [10] 。2010年，在中国运筹学大会上，师海忠提出了互连网络的正则图连通圈网络模型，设计出了多种互连网络，并提出了一系列猜想 [1] 。在此基础上，师海忠又进一步提出了k次十二面体–师连通圈网络 $DSCC\left(k\right)$ 和笛卡尔乘积网络 $DSCC\left(k\right)\times K_2$ 、 $DSCC\left(k\right)\times C_m$ ，并提出如下猜想：

猜想1：k次十二面体–师连通圈网络是Hamilton图。

猜想2：任何一个3正则3连通的Hamilton图，每个顶点用一个三角形代替后得到的图一定是Hamilton图。

猜想3：一个3正则3连通平面图的每个顶点用一个三角形来代替得到的图是Hamilton图，则原图是Hamilton图。

猜想4： $DSCC\left(k\right)\times K_2$ 是边不交的2个Hamilton圈的并。

猜想5： $DSCC\left(k\right)\times C_m$ 是边不交的2个Hamilton圈和一个完美对集的并。

2. 基本概念

定义1 [4] ：图G是一点边连续交替出现的序列， $w=v_0{e}_1{v}_1{e}_2{v}_2\cdots e_n{v}_n$ 称为图G的一个途径，其中 $$ 分别称为途径的起点和终点，w上其余顶点称为中途点，图G中边不重复出现的途径称为迹。图G中起点和终点相同的途径称为闭途径，边不重复出现的闭途径称为闭迹(也称为回路)。中途点不重复的闭途径称为圈。

定义2 [4] ：包含图G的每个顶点的圈称为图G的Hamilton圈，具有Hamilton圈的图称为Hamilton图。

定义3 [4] ：图G中与一个顶点 $v_i$ 相关联的边的数目叫做顶点 $v_i$ 的度，记作 $d\left(v_i\right)$ 或 $\mathrm{deg}\left(v_i\right)$ ，图G中所有顶点中最小的度记作 $\delta \left(G\right)=\min \left\{d\left(v\right)|v\in V\left(G\right)\right\}$ ，最大的度记作 $\Delta \left(G\right)=\max \left\{d\left(v\right)|v\in V\left(G\right)\right\}$ 。如果 $\delta \left(G\right)=\Delta \left(G\right)=k$ ，则图G中所有顶点的度相等，这时称图G是k正则的。

定义4：将十二面体连通圈网络中的每个顶点用一个三角形代替，所得到的新网络叫做1次十二面体-师连通圈网络，记为 $DSCC\left(1\right)$ ；然后再将1次十二面体–师连通圈网络中的每个顶点用一个三角形代替，得到的新网络叫做2次十二面体-师连通圈网络，记为 $DSCC\left(2\right)$ ；依次代替k次，得到的新网络叫做k次十二面体–师连通圈网络，记为 $DSCC\left(k\right)$ 。

定义5 [2] ：设 $G_1=\left(V_1,E_1\right)$ 和 $G_2=\left(V_2,E_2\right)$ 是两个无向图， $G_1$ 和 $G_2$ 的笛卡尔乘积是无向图，记为 $G_1\times G_2$ 。其中 $V\left(G_1\times G_2\right)=V_1\times V_2=\left\{\left(v_1,v_2\right)|v_1\in V_1且v_2\in V_2\right\}$ ，存在一条顶点 $x_1{x}_2$ 与顶点 $y_1{y}_2$ 之间的边(其中 $x_1,y_1\in V\left(G_1\right),x_2,y_2\in V\left(G_2\right)$ )当且仅当或者 $x_1=y_1$ 且 $x_2{y}_2\in E\left(G_2\right)$ ，或者 $x_2=y_2$ 且 $x_1{y}_1\in E\left(G_1\right)$ 。类似，可以定义笛卡尔乘积 $G_1\times G_2\times \cdots \times G_n$ 。

定义6：将k次十二面体–师连通圈网络 $DSCC\left(k\right)$ 与 $K_2$ 作笛卡尔乘积生成的新网络记为 $DSCC\left(k\right)\times K_2$ 。k次十二面体–师连通圈网络 $DSCC\left(k\right)$ 与一个长度为m的圈 $C_m$ 作笛卡尔乘积生成的新网络，我们记为 $DSCC\left(k\right)\times C_m$ $\left(k=0,1,2,\cdots ,m=3,4,\cdots \right)$ 。

3. 主要结果

3.1. k次十二面体–师连通圈网络

引理1 [4] ：十二面体DH是Hamilton图。

如图1、图2所示。

Figure 1. Dodecahedron DH

图1. 十二面体DH

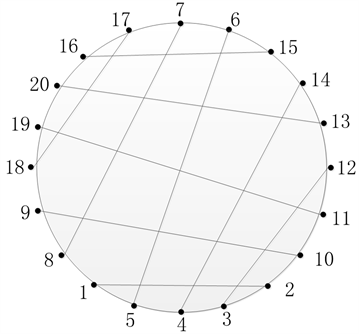
Figure 2. The ring representation of dodecahedron DH

图2. 十二面体DH的圈表示

Hamilton圈为：1-8-9-18-19-20-16-17-7-6-15-14-13-12-11-10-2-3-4-5-1。

为了统一起见，我们用 $DSCC\left(0\right)$ 表示十二面体DH。

定理1 1次十二面体–师连通圈网络 $DSCC\left(1\right)$ 是Hamilton图。

证明：如图3、图4所示。

Figure 3. DSCC(1)

图3. DSCC(1)

Figure 4. The ring representation of DSCC(1)

图4. DSCC(1)的圈表示

由图3、图4可知，Hamilton圈为：

(1,1)-(1,3)-(1,2)-(8,1)-(8,2)-(8,3)-(9,1)-(9,3)-(9,2)-(18,1)-(18,2)-(18,3)-(19,1)-(19,3)-(19,2)-(20,1)-(20,3)-(20,2)-(16,1)-(16,3)-(16,2)-(17,1)-(17,2)-(17,3)-(7,1)-(7,2)-(7,3)-(6,1)-(6,2)-(6,3)-(15,1)-(15,3)-(15,2)-(14,1)-(14,2)-(14,3)-(13,1)-(13,3)-(13,2)-(12,1)-(12,2)-(12,3)-(11,1)-(11,3)-(11,2)-(10,1)-(10,3)-(10,2)-(2,1)-(2,3)-(2,2)-(3,1)-(3,2)-(3,3)-(4,1)-(4,2)-(4,3)-(5,1)-(5,2)-(5,3)-(1,1)。

由此可知，1次十二面体–师连通圈网络 $DSCC\left(1\right)$ 是Hamilton图。

定理2：2次十二面体–师连通圈网络 $DSCC\left(2\right)$ 是Hamilton图。

证明：如图5、图6所示。

由图5、图6可知，Hamilton圈为：

(1,1,1)-(1,1,2)-(1,1,3)-(1,3,1)-(1,3,3)-(1,3,2)-(1,2,1)-(1,2,2)-(1,2,3)-(8,1,1)-(8,1,3)-(8,1,2)-(8,2,1)-(8,2,2)-(8,2,3)-(8,3,1)-(8,3,3)-(8,3,2)-(9,1,1)-(9,1,2)-(9,1,3)-(9,3,1)-(9,3,3)-(9,3,2)-(9,2,1)-(9,2,2)-(9,2,3)-(18,1,1)-(18,1,3)-(18,1,2)-(18,2,1)-(18,2,2)-(18,2,3)-(18,3,1)-(18,3,3)-(18,3,2)-(19,1,1)-(19,1,2)-(19,1,3)-(19,3,1)-(19,3,3)-(19,3,2)-(19,2,1)-(19,2,2)-(19,2,3)-(20,1,1)-(20,1,2)-(20,1,3)-(20,3,1)-(20,3,3)-(20,3,2)-(20,2,1)-(20,2,2)-(20,2,3)-(16,1,1)-(16,1,2)-(16,1,3)-(16,3,1)-(16,3,3)-(16,3,2)-(16,2,1)-(16,2,2)-(16,2,3)-(17,1,1)-(17,1,3)-(17,1,2)-(17,2,1)-(17,2,2)-(17,2,3)-(17,3,1)-(17,3,3)-(17,3,2)-(7,1,1)-(7,1,3)-(7,1,2)-(7,2,1)-(7,2,2)-(7,2,3)-(7,3,1)-(7,3,3)-(7,3,2)-(6,1,1)-(6,1,3)-(6,1,2)-(6,2,1)-(6,2,2)-(6,2,3)-(6,3,1)-(6,3,3)-(6,3,2)-(15,1,1)-(15,1,2)-(15,1,3)-(15,3,1)-(15,3,3)-(15,3,2)-(15,2,1)-(15,2,2)-(15,2,3)-(14,1,1)-(14,1,3)-(14,1,2)-(14,2,1)-(14,2,2)-(14,2,3)-(14,3,1)-(14,3,3)-(14,3,2)-(13,1,1)-(13,1,2)-(13,1,3)-(13,3,1)-(13,3,3)-(13,3,2)-(13,2,1)-(13,2,2)-(13,2,3)-(12,1,1)-(12,1,3)-(12,1,2)-(12,2,1)-(12,2,2)-

Figure 5. DSCC(2)

图5. DSCC(2)

Figure 6. The ring representation of DSCC(2)

图6. DSCC(2)的圈表示

(12,2,3)-(12,3,1)-(12,3,3)-(12,3,2)-(11,1,1)-(11,1,2)-(11,1,3)-(11,3,1)-(11,3,3)-(11,3,2)-(11,2,1)-(11,2,2)-(11,2,3)-(10,1,1)-(10,1,2)-(10,1,3)-(10,3,1)-(10,3,3)-(10,3,2)-(10,2,1)-(10,2,2)-(10,2,3)-(2,1,1)-(2,1,2)-(2,1,3)-(2,3,1)-(2,3,3)-(2,3,2)-(2,2,1)-(2,2,2)-(2,2,3)-(3,1,1)-(3,1,3)-(3,1,2)-(3,2,1)-(3,2,2)-(3,2,3)-(3,3,1)-(3,3,3)-(3,3,2)-(4,1,1)-(4,1,3)-(4,1,2)-(4,2,1)-(4,2,2)-(4,2,3)-(4,3,1)-(4,3,)-(4,3,2)-(5,1,1)-(5,1,3)-(5,1,2)-(5,2,1)-(5,2,2)-(5,2,3)-(5,3,1)-(5,3,3)-(5,3,2)-(1,1,1)。

由此可知，2次十二面体–师连通圈网络 $DSCC\left(2\right)$ 是Hamilton图。

定理3：k次十二面体–师连通圈网络 $DSCC\left(k\right)$ 是Hamilton图。

证明：当k = 0、1、2时，由引理1、定理1、2知，是Hamilton图。

假设k − 1次十二面体–师连通圈网络 $DSCC\left(k-1\right)$ 是Hamilton图，即存在Hamilton圈 $H_{k-1}$ 。

设 $v_0$ 是k − 1次十二面体–师连通圈网络 $DSCC\left(k-1\right)$ 中的任意一个顶点， $v_1,v_2,v_3$ 是与 $v_0$ 相邻的三个顶点，则Hamilton圈 $H_{k-1}$ 中必含有边 $v_0{v}_1,v_0{v}_2,v_0{v}_3$ 中的两条边。假设Hamilton圈 $H_{k-1}$ 中含有边 $v_0{v}_1,v_0{v}_2$ (其它情况证明类似)，如图7所示。

当用一个小三角形分别代替k − 1次十二面体–师连通圈网络 $DSCC\left(k-1\right)$ 中的每个顶点时，我们假设用三角形 ${\Delta }_{v_{\left(i,1\right)}{v}_{\left(i,2\right)}{v}_{\left(i,3\right)}}$ 代替顶点 $v_i\left(i=0,1,2,3\right)$ ，则 $v_0,v_1,v_2,v_3$ 四点处变化后的图 $DSCC\left(k\right)$ 如图8所示。用路 $P_k=v_{\left(1,1\right)}{v}_{\left(0,1\right)}{v}_{\left(0,3\right)}{v}_{\left(0,2\right)}{v}_{\left(2,1\right)}$ 代替Hamilton圈 $H_{k-1}$ 中的路 $P_{k-1}=v_1{v}_0{v}_2$ 后，得到的圈 $H_k$ 即为k次十二面体–师连通圈网络 $DSCC\left(k\right)$ 中的Hamilton圈。

综上所述，由数学归纳法知k次十二面体–师连通圈网络 $DSCC\left(k\right)$ 是Hamilton图。

定理4：k次十二面体–师连通圈网络 $DSCC\left(k\right)$ 的性质：

1) k次十二面体–师连通圈网络有 $20\times 3^k$ 个顶点，有 $30\times 3^k$ 条边；

2) k次十二面体–师连通圈网络 $DSCC\left(k\right)$ 是3正则3连通的；

3) k次十二面体–师连通圈网络 $DSCC\left(k\right)$ 是平面图；

4) k次十二面体–师连通圈网络是Hamilton图。

定理5：任何一个3正则3连通的平面Hamilton图 $\left(3,3\right)-HG$ ，每个顶点用一个三角形代替后得到的图 $\left(3,3\right)-HGCC\left(1\right)$ 一定是3正则3连通的平面Hamilton图。

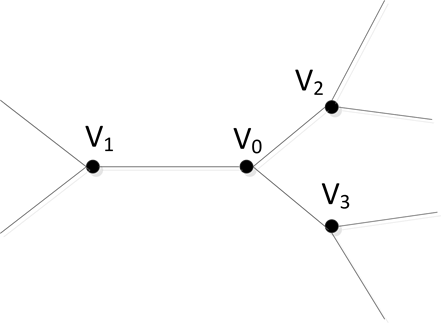
Figure 7. Local graphical representation of DSCC(k-1)

图7. DSCC(k-1)的局部图示

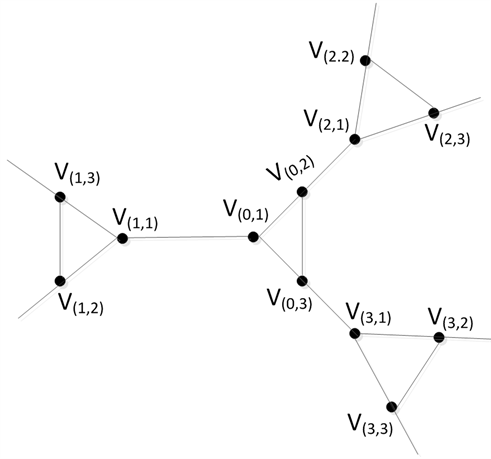
Figure 8. Local graphical representation of DSCC(k)

图8. DSCC(k)的局部图示

证明：设 $H_0$ 是任意3正则3连通平面Hamilton图 $\left(3,3\right)-HG$ 的一个Hamilton圈， $v_1$ 是 $\left(3,3\right)-HG$ 中的任意一个顶点， $v_2,v_3,v_4$ 是与 $v_1$ 相邻的三个顶点。则Hamilton圈 $H_0$ 中必含有边 $v_1{v}_2,v_1{v}_3,v_1{v}_4$ 中的两条边，假设Hamilton圈 $H_0$ 中含有边 $v_1{v}_2,v_1{v}_3$ (其它情况同理可证)，如图9所示。

当用小三角形分别代替3正则3连通平面Hamilton图 $\left(3,3\right)-HG$ 中的每个顶点时，我们假设用三角形 ${\Delta }_{v_{\left(i,1\right)}{v}_{\left(i,2\right)}{v}_{\left(i,3\right)}}$ 代替顶点 $v_i\left(i=1,2,3,\cdots \right)$ ，则 $v_1,v_2,v_3,v_4$ 四点处变化后的平面图 $\left(3,3\right)-HGCC\left(1\right)$ 如图10所示。在 $H_0$ 中，用路 $P_1=v_{\left(2,1\right)}{v}_{\left(1,1\right)}{v}_{\left(1,3\right)}{v}_{\left(1,2\right)}{v}_{\left(3,1\right)}$ 代替Hamilton圈 $H_0$ 中的路 $P_0=v_2{v}_1{v}_3$ 后，得到的圈 $H_1$ 是一个Hamilton圈。所以，任何一个3正则3连通的平面Hamilton图 $\left(3,3\right)-HG$ 的每个顶点用一个三角形代替后，得到的图 $\left(3,3\right)-HGCC\left(1\right)$ 是3正则3连通的平面Hamilton图。

定理6：一个3正则3连通平面图 $\left(3,3\right)-HGP$ 的每个顶点用一个三角形来代替得到的图 $\left(3,3\right)-HGPCC\left(1\right)$ 是Hamilton图，则：

1) 图 $\left(3,3\right)-HGPCC\left(1\right)$ 是3正则3连通的平面图；

2) 原图 $\left(3,3\right)-HGP$ 是Hamilton图。

证明：1)结论显然成立。

2) 设Hamilton图 $\left(3,3\right)-HGPCC\left(1\right)$ 中的一个Hamilton圈为 $H_1=v_{\left(1,1\right)}{v}_{\left(1,2\right)}{v}_{\left(1,3\right)}{v}_{\left(2,1\right)}{v}_{\left(2,2\right)}{v}_{\left(2,3\right)}\cdots v_{\left(n,1\right)}{v}_{\left(n,2\right)}{v}_{\left(n,3\right)}{v}_{\left(1,1\right)}$ ，其中 $v_{\left(i,1\right)},v_{\left(i,2\right)},v_{\left(i,3\right)}$ 是代替顶点 $v_i\left(i=1,2,\cdots ,n\right)$ 的三角形的三个顶点，如图11所示。

当用一个点去代替一个三角形时(可以看作是把这个三角形缩小为一个顶点)，我们假设用点 $v_i\left(i=1,2,\cdots ,n\right)$ 代替顶点为 $v_{\left(i,1\right)},v_{\left(i,2\right)},v_{\left(i,3\right)}$ 的三角形，则代替后得到的图正是原图 $\left(3,3\right)-HGP$ ，如图12所示。在 $H_1$ 中，用顶点 $v_i\left(i=1,2,\cdots ,n\right)$ 代替 $H_1$ 中的路 $P_1=v_{\left(i,1\right)}{v}_{\left(i,2\right)}{v}_{\left(i,3\right)}$ 后，得到图 $\left(3,3\right)-HGP$ 中的圈 $H_1=v_1{v}_2\cdots v_{n-1}{v}_n{v}_1$ 是一个Hamilton圈。所以，原图 $\left(3,3\right)-HGP$ 是Hamilton图。

Figure 9. Local graphical representation of (3,3)-HG

图9. (3,3)-HG的局部图示

Figure 10. Local graphical representation of (3,3)-HGCC(1)

图10. (3,3)-HGCC(1)的局部图示

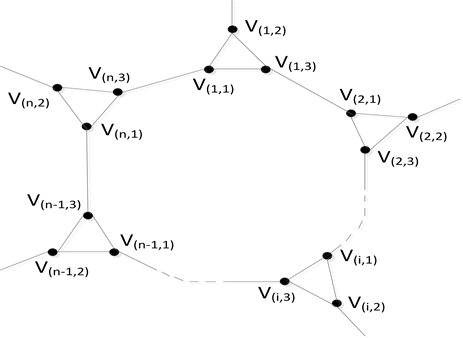
Figure 11. Local graphical representation of (3,3)-HGPCC(1)

图11. (3,3)-HGPCC(1)的局部图示

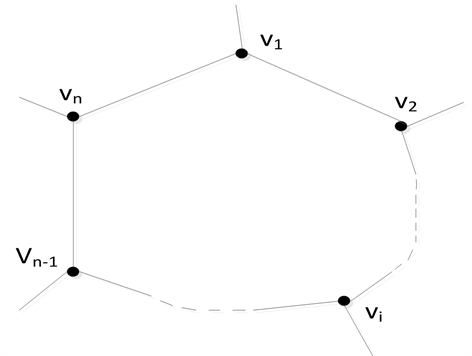
Figure 12. Local graphical representation of (3,3)-HGP

图12. (3,3)-HGP的局部图示

3.2. 十二面体连通圈网络的3维变体

在笛卡尔乘积图中，为了方便统一起见，我们用 $DSCC\left(0\right)$ 表示十二面体DH。

猜想4： $DSCC\left(k\right)\times K_2$ 是边不交的2个Hamilton圈的并。

在猜想4中，当k = 0时，笛卡尔乘积图为 $DSCC\left(k\right)\times K_2$ ，我们得到如下结论。

定理7： $DSCC\left(0\right)\times K_2$ 是边不交的1个Hamilton圈和2个完美对集的并。

证明： $DSCC\left(0\right)\times K_2$ 如图13、图14所示，我们能够找到

Hamilton圈 $H_1$ 为：

01-08-09-018-019-020-016-017-07-06-015-014-013-012-011-010-02-03-04-05-15-14-13-12-110-111-112-113-114-115-16-17-117-116-120-119-118-19-18-11-01。

完美对集 $M_1$ 为：01-02，03-012，04-014，05-06，07-08，09-010，011-019，013-020，015-016，017-018，11-12，13-112，14-114，15-16，17-18，19-110，111-119，113-120，115-116，117-118。

完美对集 $M_2$ 为：01-05，11-15，02-12，03-13，04-14，05-15，06-16，07-17，08-18，09-19，010-110，011-111，012-112，013-113，014-114，015-115，016-116，017-117，018-118，019-119，020-120。

Figure 13. DSCC(0)xK₂ after DSCC(0) ring representation

图13. DSCC(0)圈表示后的DSCC(0)xK₂

Figure 14. DSCC(0)xK₂

图14. DSCC(0)xK₂

定理得证。

引理2 [2] ：设 $G_i\left(i=1,2,\cdots ,n\right)$ 是连通图，则

$d\left(G_1\times G_2\times \cdots \times G_n\right)=d\left(G_1\right)+d\left(G_2\right)+\cdots +d\left(G_n\right)$ ，

这里 $d\left(G\right)$ 表示图G的直径。

引理3 [2] ：如果 $k\left(G_i\right)=\delta \left(G_i\right)>0,i=1,2,\cdots ,n$ ，那么

$k\left(G_1\times G_2\times \cdots \times G_n\right)=k\left(G_1\right)+k\left(G_2\right)+\cdots +k\left(G_n\right)$ ，

这里 $k\left(G\right)$ 表示图G的连通度， $\delta \left(G\right)$ 表示图G的最小度。

引理4 [2] ：如果对每个 $i=1,2,\cdots ,n$ ，均有 $k\left(G_i\right)>0$ ， $\lambda \left(G_i\right)>0$ ，那么

$k\left(G_1\times G_2\times \cdots \times G_n\right)\ge k\left(G_1\right)+k\left(G_2\right)+\cdots +k\left(G_n\right)$ ；

$\lambda \left(G_1\times G_2\times \cdots \times G_n\right)\ge \lambda \left(G_1\right)+\lambda \left(G_2\right)+\cdots +\lambda \left(G_n\right)$ ；

这里 $k\left(G\right)$ 表示图G的连通度， $\lambda \left(G\right)$ 表示图G的边连通度。

引理5 [2] ：设 $G_1$ 和 $G_2$ 是无向图， $G_1\times G_2$ 是Hamilton图当且仅当 $G_1$ 和 $G_2$ 之一是Hamilton图，而另一个含Hamilton路。

定理8：十二面体–师连通圈网络 $DSCC\left(k\right)$ 与 $K_2$ 的笛卡尔乘积网络 $DSCC\left(k\right)\times K_2$ 的基本性质：

1) $DSCC\left(k\right)\times K_2$ 有 $40\times 3^k$ 个顶点，有 $80\times 3^k$ 条边；

2) $DSCC\left(k\right)\times K_2$ 是4正则4连通的；

3) $DSCC\left(k\right)\times K_2$ 的连通度 $k\left(DSCC\left(k\right)\times K_2\right)=4$ ，边连通度 $\lambda \left(DSCC\left(k\right)\times K_2\right)=6$ ；

4) 当 $k=0$ 时， $DSCC\left(k\right)\times K_2$ 是Hamilton图。

对于猜想4：当 $k=0,1,2,\cdots$ 时， $DSCC\left(k\right)\times K_2$ 是边不交的2个Hamilton圈的并。这个结论在此处并没有得到证明，它的正确性有待我们进一步探索。

猜想5： $DSCC\left(k\right)\times C_m\left(m\ge 3\right)$ 是边不交的2个Hamilton圈和一个完美对集的并。

当 $k=0,m=3$ 时，笛卡尔乘积网络 $DSCC\left(0\right)\times C_3$ 如图15所示。

注：图中内部对应点之间的部分连线未画出。

定理9： $DSCC\left(0\right)\times C_3$ 是Hamilton图。

证明：由图15可知，Hamilton圈为：

01-08-09-018-019-020-016-017-07-06-015-014-013-012-011-010-02-03-04-05-15-16-17-18-19-110-111-112-113-120-119-118-117-116-115-114-14-13-23-24-25-21-28-27-26-215-214-213-212-211-219-220-216-217-218-29-210-22-12-11-01。

因此， $DSCC\left(0\right)\times C_3$ 是Hamilton图。

当 $k=0,m=4$ 时，笛卡尔乘积网络 $DSCC\left(0\right)\times C_4$ 如图16所示。

注：图中内部对应点之间的部分连线未画出。

定理10： $DSCC\left(0\right)\times C_4$ 是Hamilton图。

证明：由图16可知，Hamilton圈为：

01-08-09-018-019-020-016-017-07-06-015-014-013-012-011-010-02-03-04-05-15-14-13-12-110-111-112-113-114-115-16-17-117-116-120-119-118-19-18-12-11-21-28-29-218-219-220-216-217-27-26-215-214-213-212-211-210-22-23-24-25-35-34-33-32-310-311-312-313-314-315-36-37-317-316-320-319-318-39-38-31-01。

因此， $DSCC\left(0\right)\times C_4$ 是Hamilton图。

我们可以得到笛卡尔乘积网络 $DSCC\left(k\right)\times C_m\left(m\ge 3\right)$ 的一些性质如下：

Figure 15. DSCC(0)xC₃

图15. DSCC(0)xC₃

定理11：十二面体–师连通圈网络 $DSCC\left(k\right)$ 与环网络 $C_m$ 的笛卡尔乘积网络 $DSCC\left(k\right)\times C_m$ 的基本性质：

1) $DSCC\left(k\right)\times C_m$ 有 $20m\times 3^k$ 个顶点，有 $50m\times 3^k$ 条边；

2) $DSCC\left(k\right)\times C_m$ 是5正则5连通的；

3) $DSCC\left(k\right)\times C_m$ 的连通度 $k\left(DSCC\left(k\right)\times C_m\right)=5$ ，边连通度 $\lambda \left(DSCC\left(k\right)\times C_m\right)=8$ ；

4) 当 $k=0,m=3,4$ 时， $DSCC\left(k\right)\times C_m$ 是Hamilton图。

猜想5的结论是否正确，我们在以后的研究中有待进一步探索。

4. 结束语

本文给出了 $DSCC\left(k\right)$ 的定义以及一些重要的性质，证明了 $DSCC\left(k\right)$ 是Hamilton图，并对进一步提

Figure 16. DSCC(0)XC₄

图16. DSCC(0)XC₄

出的猜想2和猜想3做了证明。构建了笛卡尔乘积网络 $DSCC\left(k\right)\times K_2$ 和 $DSCC\left(k\right)\times C_m$ ，给出了它们的一些性质，但对猜想4和猜想5的结论有待进一步研究。

致谢

衷心感谢堵丁柱教授在1996年把我们带进超级计算机互连网络研究领域。