数据洞察：能源概况的历史演变和预测

Data Insights: Historical Evolution and Forecast of Energy Profile

摘要: 能量生产和使用是任何经济的主要部分。加利福尼亚州(CA)，亚利桑那州(AZ)，新墨西哥州(NM)和德克萨斯州(TX)希望形成一个现实的新的能源契约，其重点在于提高清洁和可再生能源的利用。本文认为确定能源概况就是对重要数据进行选择与汇总，同时实现数据的可视化，定性得出各州的能源概况。进而本文对其进行纵向分析，致力于发现其历史演变规律并对未来值进行预测。

Abstract: Energy production and use is a major part of any economy. California (CA), Arizona (AZ), New Mexico (NM), and Texas (TX) hope to form a realistic new energy compact that focuses on improving the use of clean and renewable energy. This article believes that determining the energy profile is to select and summarize important data, and at the same time realize the visualization of the data, and qualitatively draw the energy profiles of the states. In this paper, a longitudinal analysis of it is made to find out its historical evolution rules and predict future values.

1. 问题的引出

能量生产和使用是任何经济的主要部分。在美国，能源政策的许多层面被分散到国家层面。另外，各州不同的地质条件和产业也影响着能源的使用和生产。在1970年美国西部的12个州成立了西部州际能源契约组织(WIEC)，其任务重在促进各州之间的合作。州际契约是两个或两个以上州之间的合同安排，这些州之间就具体的政策问题达成一致，并采取一套标准或就某一地区或国家事务相互合作。沿美国和墨西哥的边境，有四个州：加利福尼亚州(CA)、亚利桑那州(AZ)、新墨西哥州(NM)和德克萨斯州(TX)，四州希望形成一个现实的新能源契约，其重点在于提高清洁、可再生能源的利用。本文将进行数据 [1] 分析和建模来发掘各州的能源概况，并进行相关的预测。

问题一：依据相关数据，为四个州分别创建相应的能源概况。

问题二：建立一个模型来尝试描述1960年至2009年四个州中每个州的能源状况是如何演变的并作预测。

问题三：确定2009年四个州中哪些州具有“最好”的清洁可再生能源使用情况。

本文数据详见：

http://www.comap.com/undergraduate/contests/mcm/contests/2018/problems/2018_MCM-ICM_Problems.zip。

2. 符号说明

表1是文章中的符号说明。

3. 原始数据检验

原始数据中的异常值可能会对模型产生不利影响，因此本文首先检查数据。考虑到后面涉及的数据格式：

,

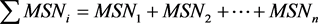所以，本文对公示左右两侧的误差进行检验

$\text{error}=\frac{{\displaystyle \sum MS{N}_i}-\left(MS{N}_1+MS{N}_2+\cdots +MS{N}_n\right)}{{\displaystyle \sum MSN}}$ ,

部分误差结果如表2所示。

Table 1. Symbol description table

表1. 符号说明表

Table 2. Raw data test results

表2. 原始数据检验结果

结合概率论与数理统计的知识，从表2的结果可以看出，误差明显低于1%，所以本文认为原始数据足够可信。

需要指出的是，本文承认原始数据与实际情况之间可能存在差异，但后文的模型是建立在公式的加和关系(即能源结构的组成关系)上，而非原始数据，所以本文进行了上述检验。

4. 模型的建立与求解

4.1. 各州能量概况

本文对已知数据进行纵向分析，使杂乱无章的数据易于理解，最后得出各州的能源概况。

4.1.1. 重要数据的选择与汇总

已知的数据文件提供了四个州605个变量的50年数据，他们是与能源的消耗、能源的生产、人口和经济相关的信息。显然能源概况是与这四个方面有关的，下面本文分别对他们进行分析。

Ø 能源的消耗量

根据美国能源信息署和数据集中变量之间的关系，本文直接找到了能源消耗总量TETCB的公式

$TETCBZZ=FFTCBZZ+NUETBZZ+RETCBZZ+ELNIBZZ+ELISBZZ$

即能源消耗总量是化石燃料消耗量、核电生产的电力、可再生能源总消费量、净进口到美国的电力和州际电力销售及相关损失五部分之和。这即是对于能源的消耗量的官方定义，但是本文也发现了TETCB所涉及数据的一些问题。

化石燃料消耗量是明显大于其余四者的，为使能源概况更加丰富，本文根据化石燃料的消耗量公式

$FFTCB=CLTCB+NNTCB+PMTCB$ ,

将化石燃料消耗量用煤炭总消费量CLTCB、天然气总消费量NNTCB和石油产品总消费量PMTCB来取代，使得TETCB中各组分占比的相对差距减小。

需要着重指出的是，对ELNIB和ELISB的处理：

1) ELNIB：对比于TETCB中的其他元素，ELNIB的数据值占比过小，均小于1%；

2) ELISB：出现负值，且数值较大；

3) 将ELNIB与ELISB从TETCB中剔除，产生新的TETCB，即

$\begin{array}{c}TETCB\left(new\right)=TETCB\left(original\right)-ELNIB-ELISB\\ =FFTCB+NUETB+RETCB\\ =CLTCB+NNTCB+PMTCB+NUETB+RETCB\end{array}$

(注：下文所指的TETCB皆指TETCB(new))。

所以，能源消耗量的重要数据即为TETCB,它包括：CLTCB、NNTCB、PMTCB、NUETB和RETCB。

另外地，如果仅考虑605个能源项目的量值无法清楚地表现能源的结构，且不利于各州州长对能源概况做出判断。所以，在后文，为更好地表现能源状况的组成结构的演变规律，本文将用到的数据从量值形式转换为百分比形式，即

$Dat{a}_1\left(percentage\right)=\frac{Dat{a}_1\left(value\right)}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}Dat{a}_i\left(value\right)}}$ ,

例如，

$\begin{array}{l}CLTCB\left(percentage\right)\\ =\frac{CLTCB\left(value\right)}{CLTCB\left(value\right)+NNTCB\left(value\right)+PMTCB\left(value\right)+NUETB\left(value\right)+RETCB\left(value\right)}\\ =\frac{CLTCB\left(value\right)}{TETCB\left(value\right)}\end{array}$

Ø 能源消耗量与经济和人口的关系

四州希望制定一个新的能源契约，重点在于提高清洁、可再生能源的利用。为达到这一目的，本文选取了TETGR和TETPB的数据(这里的数据为量值形式，而非百分比形式)。选取TETGR的原因如下：TETGR的公式为

$TETGR=\frac{TETCB}{GDPRX}$

对于美国，如果能保持GDP的持续增长，同时能源消耗总量在不断下降(此时TETGR在减小)，这就表明高耗能、低GDP贡献企业的数量在减少，低耗能、高GDP贡献的企业的数量在不断增加。也就是说明，各州的清洁、可再生能源的利用率在不断提高，能源结构在不断优化。所以，TETGR的减小可以说明四州朝着能源契约的目标在迈进。

本文选取人均能源消费总量TETPB的原因与上述选取TETGR的原因基本相同，都是使能源消耗总量在不断下降。

所以，能源消耗量与经济和人口的关系的重要数据包括：TETGR、TETPB。

Ø 能源生产量

由于涉及到能源生产量的数据很少，所以本文仅使用TEPRB(Total energy production)作为衡量能源生产的数据。

所以，能源生产量的重要数据包括：TEPRB

综上所述，本文选择与汇总的重要数据(5 + 2 + 1)包括：

5：

CLTCB, Coal total consumption;

NNTCB, Natural gas total consumption (excluding supplemental gaseous fuels);

PMTCB, All petroleum products total consumption excluding fuel ethanol;

NUETB, Electricity produced from nuclear power;

RETCB, Renewable energy total consumption.

2：

TETGR, Total energy consumed per dollar of real gross domestic product;

TETPB, Total energy consumption per capita.

1：

TEPRB, Total energy production.

4.1.2. 数据的可视化及各州能源概况简述

本文使用Python 2.7.13分别对四个州的能源消耗量TETCB的五组数据(CLTCB、NNTCB、PMTCB、NUETB、RETCB)进行了可视化处理。

Arizona (AZ)

由图1可以看出，1974年以前，石油与天然气的消耗量占能源消耗总量的主导地位。1974年以后，煤炭的消耗量不断增大，后趋于平稳，约占20%左右。1986年至今，随着核能在AZ的开发与利用，天然气与可再生能源的占比有所下降。

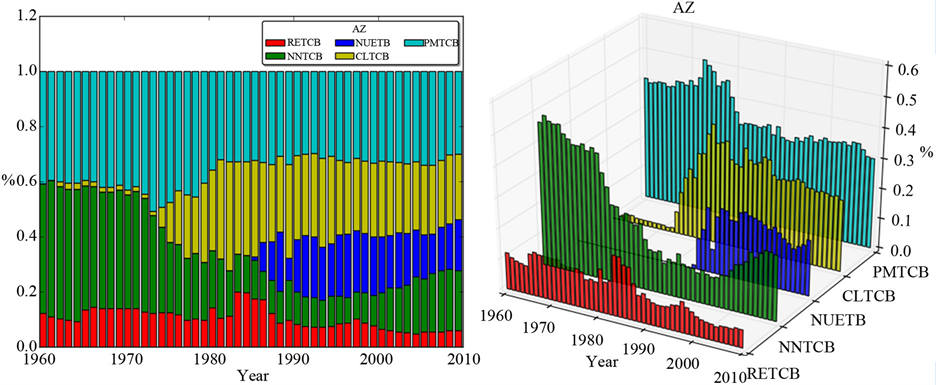
Figure 1. Energy profile of AZ (data: TETCB of AZ)

图1. 亚利桑那州的能源概况(选用数据：亚利桑那州的TETCB)

California (CA)

由图2可以看出，50年间，各部分所占比例稳定，石油一直占能源消耗总量的主导地位。特别地，CA的煤炭消耗量占比很小。核能、天然气等清洁与可再生能源占比达50%。

New Mexico (NM)

由图3可以看出，50年间，NM的化石能源消耗量占了极高的比例，高达99%，而核能和可再生能源的消耗量占比相当小，仅为1%左右。天然气的消耗量从一开始超过60%一直下降至不到40%，石油的消耗量占比稳定在30%左右。50年间，煤炭占比增至30%左右并趋于稳定。

Texas (TX)

由图4可以看出，TX的石油消耗量占比维持在40%-50%之间。与NM相似，天然气的消耗量从一开始超过60%一直下降至不到40%。煤炭为次要能源消耗，约占10%。核能和可再生能源占比很小，不到5%。

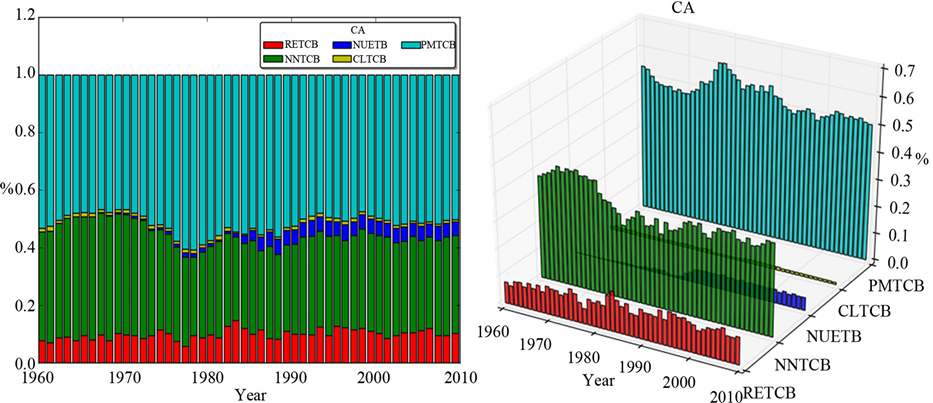
Figure 2. Energy profile of CA (data: TETCB of CA)

图2. 加利福尼亚州的能源概况(选用数据：加利福尼亚州的TETCE)

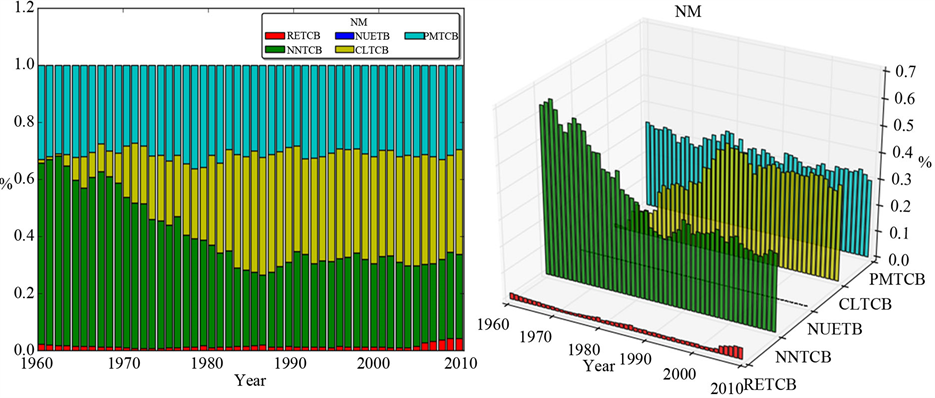
Figure 3. Energy profile of NM (data: TETCB of NM)

图3. 新墨西哥州的能源概况(选用数据：新墨西哥州的TETCB)

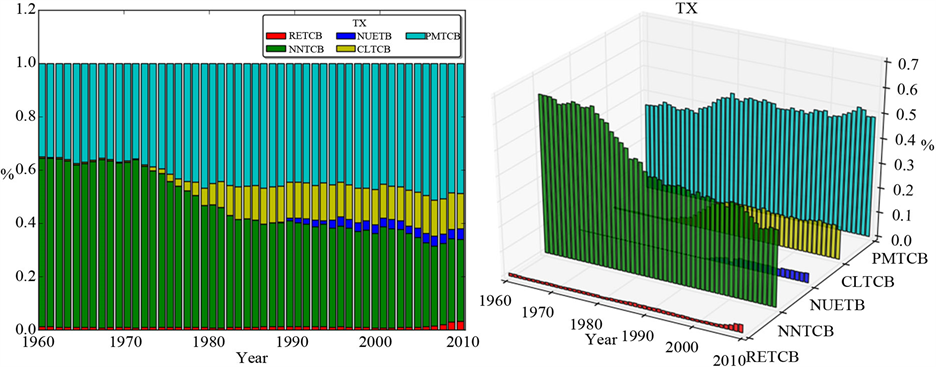
Figure 4. Energy profile of TX (data: TETCB of TX)

图4. 德克萨斯州的能源概况(选用数据：德克萨斯州的TETCB)

4.2. 能量概况的历史演变和预测

通过上述分析，本文发现各州能源概况，即重要数据“5 + 2”，属于时间序列。时间序列是时间间隔不变的数值序列，时间序列分析是通过时间序列模型研究自身的变化规律，了解长期发展趋势，通过观察历史数据来预测未来的值。

然而时间序列不同于常见的回归问题，是因为时间序列跟时间有关，而基于线性回归模型的假设为：观察结果是独立的。所以时间序列不符合线性回归模型的假设。而且马尔科夫模型并不适合解纯时间序列的问题。

针对本题本文建立ARIMA模型，对各个州的能源概况进行纵向分析。ARIMA模型的全称叫做Autoregressive Integrated Moving Average Model，也记作ARIMA(p,d,q)，是统计模型中最常见的一种用来进行时间序列预测的模型。AR是自回归, p为自回归项，MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数。该模型只需要内生变量而不需要借助其他外生变量。

4.2.1. ARIMA模型 [2]

图5是ARIMA模型的流程图。

Ø 时间序列可视化

在构建任何类型的时间序列模型之前，分析其趋势是至关重要的。由四个州的能源概况图可知，四个州的时间序列是非平稳的，很可能需要进行一阶差分，得到近似的平稳序列。

Ø 序列平稳(时间序列的预处理)

首先要对能源概况的平稳性和纯随机性进行检验，这两个重要的检验称为序列的预处理。根据检验的结果可以将序列分为不同的类型，对不同类型的序列本文会采用不同的分析方法。

· 平稳的含义

平稳就是围绕着一个常数上下波动且波动范围有限，即有常数均值和常数方差。如果有明显的趋势或周期性，那它通常是非平稳序列。检验序列是否平稳时，本文采用了自相关系数和偏相关系数。平稳的序列的自相关图和偏相关图“拖尾”或是“截尾”。“截尾”是指在某阶之后，系数都为0；“拖尾”是有一个缓慢衰减的趋势，但是不都为0。

· 将原序列转换为平稳序列

一阶差分指原序列值中相邻两个序列值之间的减法运算，k阶差分是指相距为k期的两个序列值之

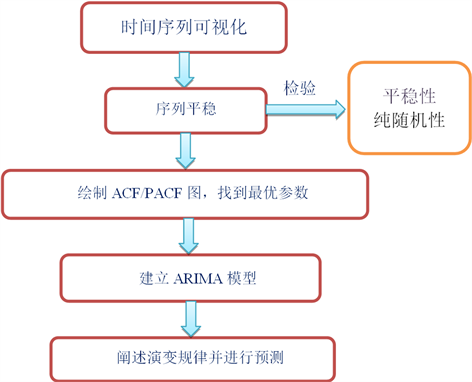
Figure 5. Flow chart of ARIMA model

图5. ARIMA模型的流程图

间相减。如果一个时间序列经过差分运算后具有平稳性，则该序列为差分平稳序列，可以使用ARIMA模型进行分析。

· 纯随机序列的处理

对于纯随机序列，又称白噪声序列，序列的各项数值之间没有任何相关关系，序列在进行完全无序的随机波动，可以终止对该序列的分析。白噪声序列是没有信息可提取的平稳序列。对于平稳非白噪声序列，它的均值和方差是常数。通常是建立一个线性模型来拟合该序列的发展，借此提取该序列的有用信息。ARIMA模型是最常用的平稳序列拟合模型。

· 绘制ACF/PACF图，找到最优参数

计算出该序列差分后数据的自相关系数(ACF)和偏相关系数(PACF)。ACF与PACF的计算结果如图6所示。

从图6中可以看出最优参数p = 0，q = 0，所以本文建立ARIMA(0,1,0)。

4.2.2. 各州能源概况的演变规律

图7中的红线(Observed)为原始数据(百分比形式)，而蓝线(Fit)为使用ARIMA模型后得到的各州可再生能源消耗量占比的演变规律(1960年到2009年)。

对AZ来说，可再生能源消耗量占总能耗的比例呈下降趋势，最高值约为18%，最低值约为5%；

对CA来说，可再生能源消耗量的占比稳中有升，从1960年的7.5%提升到2009年的10%左右，属于四州之中最大值。本文推测这可能与加利福尼亚州高科技产业汇集有关，其极高的科技力量可能对可再生能源技术的发展起推动作用；

对NM来说，尽管可再生能源消耗量的占比增长幅度较大，但仍处于较低水平，约为4%；

对TX来说，可再生能源消耗量占比也维持在较低水平，约为0.5%-3%。本文推测这可能与煤炭行业的发展有关。

Ø 四州之间的相似性

从图7中可以发现，NM和TX州的可再生能源消耗量占比的变化趋势大致相同，均为先稳定后加速上升。本文认为这可能与两周地理位置相邻这一因素有关，有助于两州在新能源方面展开合作。

Ø 四州之间的差异性

从图7及其他能源的演变规律可以发现，加利福尼亚州与新墨西哥州在各方面的差异性都很大。本

文认为这可能与该州沿海与否，人口的多与少有关。

另外地，可以发现NM和TX可再生能源演变规律的相关系数R²为0.931和0.928，很接近于1，这说明使用ARIMA模型获得的演变规律与实际的演变规律极为吻合。另外两州的相关系数也较为吻合。

4.2.3. 各州能源概况的预测

Ø 预测结果

从图8中可以看出，对于AZ来说，在未来的40年间，可再生能源消耗量占比的变化规律仍然呈现

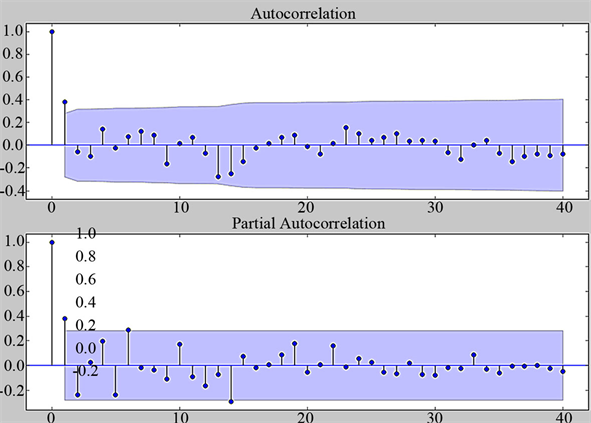
Figure 6. The result of TETPBTX’s ACF&PACF

图6. TETPBTX的自相关系数(ACF)和偏相关系数(PACF)的计算结果

*使用ARIMA模型得到的演变规律与原始数据相关系数R²分别为AZ：0.826，CA：0.454，NM：0.931，TX：0.928

Figure 7. The evolution of RETCP (percentage) in AZ, CA, NM & TX

图7. 四州RETCP (percentage)的演变图

Figure 8. The prediction of RETCP (percentage) in AZ, CA, NM & TX

图8. 四州RETCP (percentage)的预测值

下降趋势(与过去50年的趋势相同)，而这与州际契约的目标(提高清洁、可再生能源利用的占比)相违背，所以AZ亟需制定一个新能源政策，以提高在2025年和2050年时间节点的可再生能源的利用率。

对于CA州，可再生能源消耗量占比的变化规律保持了上升的趋势：RETCB在2025年将达到11%左右，在2050年将达到13%左右。这说明即使CA州不做出政策的调整，其可再生能源的占比也将可能满足能源契约的要求。所以，CA能有效降低化石能源的消耗和二氧化碳的排放，提高清洁、可再生能源的利用。

对于NM和TX这两个州，在未来的40年内，他们的可再生能源消耗量占比基本上在经历了小幅增长之后，分别在6%和4%附近保持不变。

4.3. 哪个州具有“最好”的清洁、可再生能源使用情况

本文考虑到关于“能源消耗量与经济和人口的关系”的两组数据：TETGR、TETPB。当其值减小时，能源结构在不断优化。同时，当煤炭和石油的消耗量这两组数据值越小(清洁、可再生能源的利用率越高)时，能源结构也在不断地优化。

所以，为解决哪个州有“最好”的清洁、可再生能源使用情况这个问题，本文对CLTCB、PMTCB、TETGR、TETPB的相关数据进行处理，得出相关结论。

为使不同单位的数据具有可比性，本文定义了 $C_2$ 、 $P_2$ 、 $T{R}_2$ 、 $T{B}_2$ 和 $S_b$ 五个量：

$\begin{array}{l}T{R}_1\left(x\right)=\frac{\text{TETGR}\left(x\right)}{{\displaystyle \sum \text{TETGR}\left(x\right)}},x=\text{AZ},\text{CA},\text{NM},\text{TX}\\ T{B}_1\left(x\right)=\frac{\text{TETPB}\left(x\right)}{{\displaystyle \sum \text{TETPB}\left(x\right)}}\\ C_2\left(x\right)=\frac{\text{CLTCB}\left(x\right)}{\max \text{CLTCB}}\\ P_2\left(x\right)=\frac{\text{PMTCB}\left(x\right)}{\max \text{PMTCB}}\end{array}$

Table 3. The result of the normalized model

表3. 归一化的结果

$\begin{array}{l}T{R}_2\left(x\right)=\frac{T{R}_1\left(x\right)}{\max T{R}_1\left(x\right)}\\ T{B}_2\left(x\right)=\frac{T{B}_1\left(x\right)}{\max T{B}_1\left(x\right)}\\ S_b\left(x\right)=\min (C_2\left(x\right)+P_2\left(x\right)+T{R}_2\left(x\right)+T{B}_2(x))\end{array}$

其中， $T{R}_1\left(x\right)$ 与 $T{B}_1\left(x\right)$ 的目的是将初始数据转换为百分比形式，而 $C_2\left(x\right)$ 、 $P_2\left(x\right)$ 、 $T{R}_2\left(x\right)$ 、 $T{B}_2\left(x\right)$ 的目的是将数据的大小都统一到0~1之间，使最终的 $S_b\left(x\right)$ 有意义： $S_b\left(x\right)$ 的值越小，清洁、可再生能源利用率越高，能源结构越好。

所以，由上表3可知，CA具有“最好”的清洁、可再生能源使用情况。

5. 结语

本文对重要数据进行选择与汇总，并实现可视化，从而发现各州定性的能源概况。进一步的，本文对其进行纵向分析，考察其历史演变规律并对未来值进行了预测。