1. 引言
行人检测是图像处理和计算机视觉领域中的研究热点,具有广阔的应用前景,例如智能公共安全、车辆辅助驾驶、人体行为分析、人机交互、机器人视觉导航等。目前有很多学者和研究机构热衷于行人检测的研究,有许多算法被提出,例如基于图像低层信息(颜色、形状、纹理等)的方法,Oren等 [1] 提出的Haar行人特征描述子,利用水平、垂直、对角线三个方向的小波在不同尺度上提取特征。Ojala等 [2] 提出的LBP是用于纹理分类的特征提取方法。Tuzel等 [3] 利用多种不同特征的协方差矩阵来描述行人的局部特征。由于统计机器学习具有良好的函数学习和泛化能力,基于统计机器学习的行人检测方法是目前研究的热点,例如Szaras等 [4] 利用卷积神经网络,通过学习算法自动选取分类特征。Grubb等 [5] 利用两个SVM分类器进行行人检测。Viola等 [6] 利用矩阵特征、AdaBoost和级联分类器实现了行人检测。还有一些算法将人体看成部位(头部、躯干、上肢和下肢)分类器进行行人检测,例如Mohan等 [7] 将人体划分4个部分,将各个部分的分类器作为SVM的输入,建立一个组合的多层次的分类器检测行人。Felzenszwalb等 [8] 基于图案结构模型,将滑动窗口与部位法相结构检测行人。Ali等 [9] 利用Adaboost将姿态估计和特征选择结合的方法来实现行人检测。近年来采用深度学习进行行人检测的方法相继被提出,例如Jung等 [10] 提出了用指导网络来协助训练深度卷积神经网络来提高行人检测的准确性。Tomè等 [11] 提出了一种基于深度学习的行人检测系统。
本文提出一种基于优化图的半监督学习的行人检测算法,首先提取每幅图像的形状上下文特征,并采用选择性搜索提取出行人候选区域建议框,然后融合包含行人的建议框之间距离尽量小,而不包含行人的建议框和包含行人的建议框之间的距离尽量大的先验知识构建一种优化图的半监督行人检测模型,利用该模型对图像的行人进行检测。
2. 图的半监督学习理论
半监督学习算法是指给定一组训练样本,包括已标记的样本
和未标记的样本
,通过对训练样本学习得到一个函数
,使得基于该函数得到的决策函数在所有的点上预测准确。为了能够利用未标注样本所提供的有用信息,使学习模型得到理想的效果,半监督学习需要满足群聚假设和流形假设来进行机器学习。群聚假设是指聚在一起的样本点应该具有相同的类别。流形假设是指所有样本点基本上落在一个低维的流形面上,沿着流形相近的点具有较高的相似性。满足群聚假设和流形假设的半监督学习模型可以通过一个图的方法来表示出来,采用图的方法来逼近流形,利用图的理论来求解 [12] [13] 。
通过图的拉普拉斯矩阵的正则化方法介绍图的半监督学习算法的工作过程。
定义无向图的相似度矩阵W,其中wij表示样本i和样本j的相似度,一般通过一个距离度量
和正参数σ来定义,通过调整正参数σ来达到更好的效果:
(1)
图的拉普拉斯矩阵定义为:
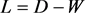 (2)
(2)
其中,D是对角阵,第(i, i)个元素为矩阵W的第i行的和,即
。
为了使机器学习f(xi)所有已标记点上取值接近于其真实值,选取合适的损失函数
来惩罚预测值和真实值之间的差异,即一个好的分类器要求损失最小化:
(3)
其中,yi是训练样本的准确值,f(xi)是分类器的预测值。
基于图的正则化项定义为:
(4)
基于图的拉普拉斯半监督学习的正则化框架定义为:
(5)
上面的正则化框架中共有两项,第一项表示样本在图上的平滑性,第二项表示损失函数。
3. 基于优化的半监督学习的行人检测算法
3.1. 特征提取和行人候选区域选取
在人类视觉中,行人的轮廓特征为人类视觉识别物体提供了重要信息,即使在背景非常复杂的环境下或目标信息不是很完整的情况下,人类也可以轻易、准确的依据轮廓特征识别出行人,所以行人的轮廓特征是视觉识别重要的特征之一,可以为识别行人提供稳定和有效的信息。其中形状上下文特征(shape context, SC)方法是物体轮廓的重要描述方法之一 [14] [15] ,它以目标轮廓的有限点集合表示物体特征。形状上下文特征原理简单、易于实现,并且实验也证明了在自适应选取边界点的基础上,利用形状上下文特征计算得到的相似度可较好地反映图像目标类别,具有较强的可分性。
形状上下文特征方法在对目标图像进行轮廓检测的基础上,选择轮廓上的一组离散的有限点的集合
表示物体,然后对于所选取的离散点集p中的任意一个点pi,计算与p中其他n − 1个点在图像形状中的相对位置关系,即以图像中特征点pi为坐标原点进行对数极坐标变换,假设以特征点pi为坐标原点,极坐标的半径上有nr个直方图区间(bin)和nθ个角度方向上的直方图区间,并且把边界方向也加入到了直方图的采样维度中,假设有ne个边界方向上的直方图区间,那么就构成了
个区间,然后计算落在特征点pi每个区间中的边界点的数目hi(k),这样就得到了特征点p的形状上下文特征,可以把其定义为:
(6)
类似,把p中的每个点表示成一组向量,就可以描述出目标图像的整个形状上下文特征。
选择性搜索(Selective Search) [16] 是一种基于设计好的低级特征的区域建议框提取方法,是目前最流行的区域建议框提取方法之一。本文采用该方法对原始图像提取出行人候选区域建议框,然后根据行人候选区域建议框映射到图像的特征图上,在特征图中找到行人候选区域建议框对应图像的形状上下文特征。
3.2. 优化图的半监督学习模型的构建
3.2.1. 构建优化图的半监督行人检测模型
设给定l个已标注训练样本
和u个未标注训练样本
,其中
,d为样本的维数。设训练样本中的前l+个为已标注的正样本
,中间的l−个为已标注的负样本
,后u个为未标注样本
。−令
,表示已标注训练样本总数。令n = l + u,表示训练样本总数。一般令
表示xi的准确标注,其中对于已标注的正样本
,令yi = 1;对于已标注的负样本
,令yi = −1;对于未标注样本
,令yi = 0。
为了提高行人检测的准确率,挖掘训练样本中具有行人的样本之间距离会较小,而具有行人的样本和不具有行人的样本之间距离会较大的知识,为构造行人检测提供有效的信息。具有行人样本之间的距离尽量小的优化问题为:
(7)
具有行人的样本和不具有行人的样本之间距离尽量大的优化问题为:
(8)
公式(7)和公式(8)协同工作得到的优化目标函数可刻画为
(9)
其中,hi,j代表样本xi和样本xj是否同类型,如果样本xi和样本xj同为正样本或同为负样本,
;如果样本xi和样本xj一个是正样本一个是负样本,
;其它
,即
(10)
把训练样本中具有行人的样本之间距离会较小,而具有行人的样本和不具有行人的样本之间距离会较大的知识作为判别的先验知识引入到图的半监督学习模型中,得到优化目标函数
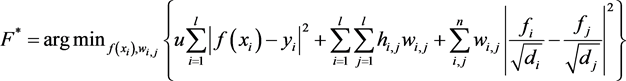 (11)
(11)
其中,D为对角阵,第(i,i)个元素为矩阵W第i行的和,即
,F*为优化图半监督模型的优化函数。上面的优化模型中共有三项,第一项表示损失函数,第二项表示样本之间的距离,第三项表示样本在图上的平滑性。
3.2.2. 优化图的半监督行人检测模型的分析
对公式(11)模型求解要比传统的图的半监督学习求解复杂,因为传统的半监督学习模型中优化的目标函数只求解f(x),而在本文中,优化的目标函数中除了求解f(x)外,相似矩阵W也是求解的一部分。对优化模型的解法分析是先对W进行最小优化处理,得到的W的优化解后再用迭代正则化方法求解f(x)。
对于W进行最小优化处理的算法如下所示:
选取优化W的训练样本
,
,优化的目的是得到一个函数
。假设
可以限制在一个不太复杂的函数类中,可以用输入量线性表示 ,解决这一优化问题就变为寻找尽可能满足
的
。实际上解决这个问题的一个直观方法是用一个线性函数来回归(拟合、逼近)样本点。支持向量回归机具有非常好的非线性拟合能力,能够成功的应用于函数逼近方面,所以利用支持向量回归机解该函数,采用硬
-带支持向量回归机方法,原问题转化为
,解决这一优化问题就变为寻找尽可能满足
的
。实际上解决这个问题的一个直观方法是用一个线性函数来回归(拟合、逼近)样本点。支持向量回归机具有非常好的非线性拟合能力,能够成功的应用于函数逼近方面,所以利用支持向量回归机解该函数,采用硬
-带支持向量回归机方法,原问题转化为
(12)
采用最大间隔法的特征,可以表示为如下的原始优化问题
(13)
其中,
是事先取定的一个正数,
不敏感损失函数的含义是,当真实值与预测值之差不超过事先给定的
时,则认为在该点的预测值是无损失的。
使用拉格朗日乘子法将其转化为对偶问题。对于公式(13)的每个约束引入拉格朗日乘子,得到如下拉格朗日函数
(14)
其中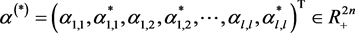 称为Lagrange乘子。
称为Lagrange乘子。
由极值条件:
,
得到
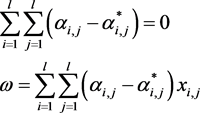 (15)
(15)
将上式代入拉格朗日函数,则原始的优化问题转化为如下的对偶问题(使用极小形式)
(16)
求解上述对偶问题,得到回归函数:
(17)
得到两个样本之间的距离预测函数
后,用该函数计算训练样本中两个样本之间的距离
作为训练样本两点之间的相似度,即得到无向图的相似度矩阵
,图的拉普拉斯矩阵定义为
 (18)
(18)
其中D是对角阵,其中
元素为矩阵
第i行的和,即
。然后,把得到的
和D带入到公式(11)中,得到如下结果
(19)
最后,用图迭代的方法求解公式(19)。
4. 实验结果及分析
为了验证算法的性能,本文选用二组数据集进行实验,一组是TUD行人数据库,该数据库的训练集提供了行人的矩形框信息、分割掩膜及其各部位(脚、小腿、大腿、躯干和头部)的大小和位置信息,训练集的正样本为1092个图像,负样本为192个非行人图像,测试集有508个图像;另一组是为了检测算法在实际应用中的性能,从《美丽心灵》、《老友记》等影视剧中选取200张图像帧作为测试数据,其中150张是有行人的图像,50张为没有行人的图像。
查全率(recall)和查准率(precision)能够很好的评价算法的错误检测和漏检测情况,所以本文采用查全率和查准率检测算法的性能,查全率和查准率分别定义如下:
(20)
(21)
其中,Nc为正确的检测数量,Nm为漏掉的检测数量,Nf为错误的检测数量。好的标注算法应该具有较高的查全率和查准率。
实验中形状上下文特征提取的相关参数取值为:极坐标半径上的直方图区间r取值2;角度方向上的直方图区间θ取值12;边界方向上的直方图区间e取值为4(分别是边缘方向为0˚,45˚,90˚,135˚),这样每一个特征点的形状上下文由2 × 12 × 4 = 96个区间来描述,如图1所示。为了表达清晰,我们把图1的对数极坐标直方图转化为图2的形式,一个格代表形状上下文的一个区间。
在实验中,对于优化的图的半监督学习,我们首先规定训练样本中两个样本之间的距离为0或1,

Figure 1. Log-Polar Transformation. (a) Direction of 0˚ Log-Polar Transformation; (b) Direction of 45˚ Log-Polar Transformation; (c) Direction of 90˚ Log-Polar Transformation; (d) Direction of 135˚ Log-Polar Transformation
图1. 对数极坐标变换图。(a) 方向为0˚边缘的对数极坐标变换图;(b) 方向为45˚边缘的对数极坐标变换图;(c) 方向为90˚边缘的对数极坐标变换图;(d) 方向为135˚边缘的对数极坐标变换图

Figure 2. Log-Polar coordinate histogram
图2. 对数极坐标直方图
如果两个样本都是正样本,则样本之间的距离为0;如果两个样本是异样本,则样本之间的距离为1,然后对样本进行学习,得到样本之间的距离预测函数,再用预测函数对训练样本集进行计算得到样本之间的距离矩阵,最后用优化图的半监督学习算法对训练样本进行训练,得到行人检测模型。
为了验证基于优化图的半监督学习的行人检测算法的性能,选取基于图的拉普拉斯半监督学习方法(GLSS)的行人检测算法进行了比较。基于图的拉普拉斯半监督学习的行人检测算法同样采用图像的形状上下文特征作为图像的特征,用基于图的拉普拉斯半监督学习进行行人检测,用SC + GLSS表示该算法。实验结果比较如表1所示。从表中可以看出用本文提出的算法对行人检测的平均准确率高于用图的拉普拉斯半监督学习的平均准确率,所以通过挖掘训练样本中具有行人的样本之间距离会较小,而具有行人的样本和不具有行人样本之间的距离会较大的先验知识可以有效地提高行人检测的准确率。
为了测试算法的性能,本文也选取了传统的HOG + SVM行人检测算法与本算法进行比较。传统的HOG + SVM行人检测算法是目前行人检测的经典方法。实验结果比较如表2所示。从表2中可以看出本文提出的行人检测算法具有一定的准确性。

Table 1. Experiment Comparison with SC + GLSS
表1. 本算法与SC + GLSS的实验比较

Table 2. Experiment Comparison with HOG + SVM
表2. 本算法与HOG + SVM的实验比较
5. 结束语
本文提出一种新的基于优化图的半监督学习的行人检测算法。该算法使用形状上下文特征作为视觉特征,考虑目前机器学习算法中普遍存在训练数据不足和忽略了类间和类内信息问题,提出结合具有行人的建议框之间距离会较小,而含有行人的建议框和不含行人的建议框之间距离会较大的先验知识构建一个优化图的半监督机器学习模型,通过构建的优化的半监督学习模型对行人检测进行学习和检测,实验结果表明本算法对行人检测具有一定的准确性。
基金项目
浙江省大学生科技创新活动计划暨新苗人才计划(2017R424001);浙江省自然科学基金(LY18F010020);浙江省重点研发计划项目(2018C01086)。