1. 引言
本解析函数边值问题是复变函数理论中的一个重要分支,其不仅在若干基础数学和数学物理领域有深刻应用,而且与力学和工程技术的实际问题有着紧密的联系和广泛的应用。
在 [1] 中路见可教授对Riemann边值问题有详尽而细致的讨论,然而从实用的观点来看,周期边值问题将更为重要。在较早期的研究中 [2] ,给出了周期Riemann边值问题在弹性力学、求解奇异积分方程等方面的应用。近些年来,可积系统的Riemann-Hilbert技术发展迅速,该理论需要处理拟周期解析函数的边值问题 [3] 。
所谓以
为拟周期的函数满足
[4] [5] [6] ,当
为无理数时,问题的情况十分复杂,本文研究
时的情形,即半周期问题。
接下来我们将着重讨论半周期Riemann边值问题的解法并给出可解条件,对问题的解提出不同的要求进行讨论,进而给出一些结论。
2. 半周期Riemann边值问题的提法
记
,考虑如图1所示的以
为周期合同的光滑封闭曲线组
,
。
半周期Riemann边值问题的提法:求一个以
为半周期的分区全纯函数
,光滑封闭曲线组
,
。各
取逆时针向为正方向。各
的内域记为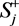 ,在
中的补域记为
,从而L的内域为
,L的外域为
,且使得
,在
中的补域记为
,从而L的内域为
,L的外域为
,且使得
(2.1)
其中
于L上,C表示复数域,且满足条件:
(2.2)

Figure 1. A class of smooth closed curves of periodic congruence
图1. 周期合同的光滑封闭曲线组
也就是说
是以
为周期的,而
是以
为半周期的。如果
,我们称此问题为正则的,否则为非正则的。如果
,则称此问题为齐次的,否则称为非齐次的。为方便叙述,我们只讨论正则的半周期Riemann边值问题。
3. 转化为周期Riemann边值问题
首先我们分析以
为半周期的函数
的性质,我们可以看到,
(3.1)
也就是说一个以
为半周期的函数
一定是以
为周期的函数。故f一般有展开式:
(3.2)
若要其满足半周期的条件,即
,我们得到
(3.3)
故(3.2)式中偶次项系数为0,即有
(3.4)
设
,则(3.4)式可改写成
,k为奇数。
如果
(3.5)
称
在
处是m (
)阶的;
如果
(3.6)
称
在
处是n (
)阶的。
这样我们可以利用周期延拓的方法将一个半周期的函数转化为一个周期的函数。那对于半周期Riemann边值问题,我们自然会想到利用已有的关于周期问题的结果来求解。
回到半周期Riemann边值问题,现在我们取基本域
来进行讨论,此时跳跃曲线为
。利用周期延拓,我们可以得到以
为周期的函数
,即
则相应的
分别转化为
为周期的
,
但应注意此时,跳跃曲线应为
,其中
表示延拓后在
中相应的曲线。此时原问题则转化为:求以
为跳跃曲线的分区全纯函数
,满足下列条件:
(3.7)
这样我们得到了一个以
为周期关于
的周期Riemann边值问题。我们仍引用文献 [1] 中对于指标的定义。我们用
表示问题(2.1)的指标,即 ,则此时对于问题(3.7),结合指标的性质,这样我们知道问题(3.7)的指标应为
。但这两个问题的解之间有着怎样的联系呢?我们设半周期问题(2.1)有解为
,其有展开式
,则此时对于问题(3.7),结合指标的性质,这样我们知道问题(3.7)的指标应为
。但这两个问题的解之间有着怎样的联系呢?我们设半周期问题(2.1)有解为
,其有展开式
(3.8)
结合半周期条件
,我们得到
(3.9)
若上式成立则k只能为奇数,其仍是以
为周期的,所以它也是周期Riemann边值问题(3.7)的解,这样我们得到:
定理1:当(3.9)式中k为奇数时,问题(2.1)和问题(3.7)是等价的。
这样我们看到问题(3.7)是加了限制条件的周期Riemann边值问题,半周期问题的解一定是周期问题的解,反之则不成立。
接下来我们列出一个关于半周期跳跃问题的引理。以
为半周期的跳跃问题为:求以光滑封闭曲线组L为跳跃曲线、以
为半周期的分区全纯函数 ,满足条件:
,满足条件:
(3.10)
其中
,且
,
在 处是m阶的。
处是m阶的。
引理1:问题(3.10)的一般解为
,
其中
为任意的次数不超过m的奇数次三角多项式。
证明:首先我们注意到
(3.11)
且
是关于
的Hölder连续函数,又由
。设
(3.12)
则
为t和z的Hölder连续函数。
现在设
,由带参数的Plemelj公式 [1] ,可以想见,
(3.13)
(3.14)
结合(3.11)和(3.12),我们得到
(3.15)
(3.16)
则
,且可以验证 。
。
 (3.17)
(3.17)
这样我们得到
(3.18)
又由
在
处是m阶的,利用一般Riemann跳跃问题的结果 [1]、(3.5)和(3.18)得到
其中
为任意的次数不超过m的奇数次三角多项式,
证毕。
4. 问题的求解
下面我们来讨论半周期Riemann边值问题的求解。
第一种情况:限定
。由上一节的讨论我们知道,此时问题(2.1)可以转化为问题(3.7),结合典则函数的性质我们知道,这时问题(3.7)中的典则函数对问题(2.1)仍是适用的。由 [1] 中的结果知,典则函数为:
(4.1)
其中
(4.2)
且
是以
为周期的函数。
这样对齐次问题(2.1)有
(4.3)
我们得到齐次问题(2.1)的一般解为
(4.4)
再考虑问题(2.1)中半周期条件,若要使
成立,结合(4.1) (4.2) (4.4)可知,此时问题只有零解且满足限定条件
,故此时齐次半周期Riemann边值问题(2.1)只有零解。因此有如下结论:
定理2:对于齐次半周期Riemann边值问题(2.1),在要求
,齐次半周期Riemann边值问题(2.1)只有零解。
第二种情况:要求
,
为整数,即要求
分别在
处有有限阶,这次我们不作齐次的要求。类似第一种情况的讨论,问题(2.1)仍可以转化为问题(3.7),则典则函数(4.1)仍然适用,问题的指标为
,
满足条件
,这样问题(2.1)变为
(4.5)
利用引理1,又由
有界,结合
的要求,我们有
(4.6)
其中
分别为
次多项式。
再考虑半周期条件,要使(3.7)满足半周期条件,因为
是以
周期的,
是以
为半周期的,所以对多项式
应有进一步的要求。由(3.5)和(3.6)式,我们知道
应具有如下形式:
(4.7)
同理得到
(4.8)
这样我们得到
定理3:如果要求
,
为整数,则问题(2.1)有解(4.6),其中
分别由(4.7)和(4.8)式给出。
5. 结论
本文给出了半周期Riemann边值问题在对
处做两种不同的要求的情形下的解的情况的分析,分别得出在要求条件下的解的封闭形式。当然我们还可以对 作其它的要求而进行讨论,而相应的解的形式也会有所不同。对于拟周期的边值问题仍有很多有意义的问题值得讨论,后续仍有很多问题值得我们关注。
作其它的要求而进行讨论,而相应的解的形式也会有所不同。对于拟周期的边值问题仍有很多有意义的问题值得讨论,后续仍有很多问题值得我们关注。
致谢
感谢在论文撰写期间对我提出指导和帮助的老师,感谢各位审稿专家的辛勤工作和指导,感谢国家自然科学基金的支持。
基金项目
国家自然科学基金,编号NSFC11501414。