基于ARIMA模型下的能源生产问题

The Problem of Energy Production Based on ARIMA Model

摘要: 我们首先通过时间序列观测，对序列的平稳性进行识别，然后对数据进行平稳化处理，最后确定以ARMA模型来分析美国与墨西哥边境上四个州(加利福尼亚州(CA)，亚利桑那州(AZ)，新墨西哥州(NM)和德克萨斯州(TX))的能源分布演变规律。

Abstract: We first identify the stability of the sequence by time series observation, and then make a smooth processing of the data, and finally determine an ARMA model to analyze the four states on the border with Mexico (California State (CA), Arizona, State (AZ), New Mexico State (NM) and Dexa Wales (TX)) Energy distribution evolution Law.

1. 引言

能源生产和使用是任何经济的主要部分。在美国，能源政策的许多方面分散到国家层面。此外，不同国家的不同地区和行业也影响能源使用和生产。本文以美国的加利福尼亚州(CA)，亚利桑那州(AZ)，新墨西哥州(NM)和德克萨斯州(TX)四个州为例，介绍一种探究能源分布的模型。

2. 改进的ARIMA模型

2.1. 时间序列分析法

时间序列分析法利用数据的自相关性建立相对最优的模型来分析客观现象的动态特征 [1] 。时间序列分析主要有确定性变化分析和随机性变化分析。其中，确定性变化分析包括趋势变化分析、周期变化分析、循环变化分析。随机性变化分析：有AR、MA、ARMA模型等 [2] 。

2.2. ARIMA模型的基本原理

ARIMA模型全称为自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model，简记ARIMA)，其中ARIMA(p,d,q)称为差分自回归移动平均模型，AR是自回归，p为自回归项；MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数 [3] 。

所谓ARIMA模型，是指将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。ARIMA模型根据原序列是否平稳以及回归中所含部分的不同，包括移动平均过程(MA)、自回归过程(AR)、自回归移动平均过程(ARMA)以及ARIMA过程。

一般的p阶自回归过程AR(p)是

$X_t={\varphi }_1{X}_{t-1}+{\varphi }_2{X}_{t-2}+\cdots +{\varphi }_p{X}_{t-p}+{\mu }_t$

其中 ${\mu }_t$ 是误差项。

一般的q阶的移动平均过程MA(q)可以表示为

$X_t={\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-{\theta }_2{\epsilon }_{t-2}-\cdots -{\theta }_q{\epsilon }_{t-q}$

将纯AR(p)与纯MA(q)结合，得到一个一般的自回归移动平均过程ARMA(p,q)

$X_t={\varphi }_1{X}_{t-1}+{\varphi }_2{X}_{t-2}+\cdots +{\varphi }_p{X}_{t-p}+{\mu }_t+{\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-{\theta }_2{\epsilon }_{t-2}-\cdots -{\theta }_q{\epsilon }_{t-q}$

3. ARIMA模型求解过程

3.1. 时间序列观测

根据时间序列的散点图、自相关函数和偏自相关函数图以ADF单位根检验其方差、趋势及其季节性变化规律，对序列的平稳性进行识别。

根据题目附件提供的数据，通过软件可以画出每个州的能源总消费、清洁可再生能源总消费和化石能源总消费数据情况，如图1。

图1中，CLTCB代表煤炭消费总量，NNTCB代表天然气总消费量，PMTCB代表所有石油产品的总消费量，RETCB代表可再生能源总消费，NUETB代表核电产生的电力。

我们以AZ州中CLTCB为例详细求解如下：

根据图1 AZ中CLTCB的曲线走势可以明显观察到，CITCB的数量逐年增加，所以数据序列是非平稳的，则需要对数据进行平稳化处理。

3.2. 平稳化处理

为了使该时间序列更容易变得平稳，首先对该序列EC取对数，令x = log(EC)，观察发现一阶差分后该模型变得平稳。我们采用EVIEW8.0软件对模型进行严格单位根检验，结果如表1。

我们发现，一阶差分后模型通过了单位根检验，拒绝存在单位根的假设，说明模型在一阶差分后平稳。因此可以对模型定阶为d = 1。

3.3. 确定模型类型

若平稳序列的偏相关函数是截尾的，而自相关函数是拖尾的，可断定序列适合AR模型；若平稳序列的偏相关函数是拖尾的，而自相关函数是截尾的，则可断定序列适合MA模型；若平稳序列的偏相关函数和自相关函数均是拖尾的，则序列适合ARMA模型。

首先使用EVIEW8.0软件对取对数后的时间序列X进行一阶差分后，对其进行自相关和偏相关分析，如图2。

根据图2，我们得到该平稳序列的自相关函数与偏相关函数均是拖尾的，则该模型适合ARMA模型。

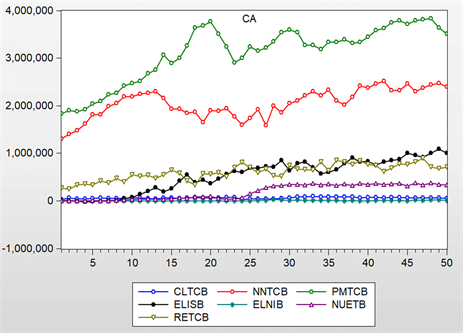
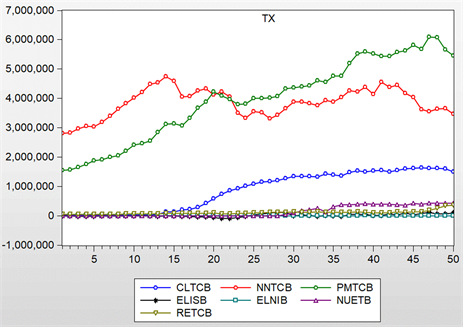
Figure 1. Energy consumption in the states

图1. 各州能源消费情况

Table 1. Unit root test of energy consumption

表1. 能源消费情况的单位根检验

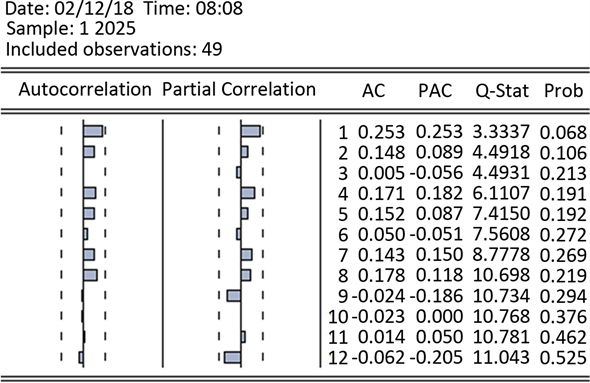
Figure 2. Self-correlation and partial correlation analysis of sequence X first-order Difference

图2. 序列X一阶差分后的自相关与偏相关分析

3.4. 进行参数估计，检验是否具有统计意义

根据上图中偏相关函数(PACF)可以看出AR(p)中p可以选择1或者选择2；根据自相关函数(ACF)可以看出MA(q)中q可以取1或者2。

根据上面p与q的取值，对一阶差分的时间序列，我们可以选择ARMA(1,1)、ARMA(1,2)、ARMA(2,1)、ARMA(2,2) 4重模型。然后将4个模型的拟合估计结果如表2。

比较表2发现，从系数的T检验和伴生概率来看，模型AR(2)MA(2)的AIC值和SC值最小，并且R²的值最大，所以我们选择AR(2)MA(2)模型 [4] 。

3.5. 模型拟合

设 $Y_t$ 为X的一阶差分，则对EC的ARIMA(2,1,2)模型可以拟合如下

$Y_t=0.207Y_{t-1}+0.6835Y_{t-2}-0.5145{\epsilon }_{t-1}-0.9742{\epsilon }_{t-2}+{\mu }_t$

其中 $Y_t=\Delta X$ 且 $X_t=\log \left(\text{EC}\right)$ ， ${\mu }_t=0.27$

故模型拟合结果为 $\text{EC}=\text{exp}(Yt)$

3.6. 假设检验，诊断残差

为检验模型的正确与合理性，用EVIEWS8.0作图如图3。

图3中红线表示CLTCB的实际值，绿线表示预测值，蓝线表示两者的残差。由图可以得到残差小于0.15所以诊断残差序列为白噪声，从而得到该模型为有效的反映了AZ州中CLTCB分布的演变规律。

Table 2. Comparison of the results of the fitting estimates of four models

表2. 四种模型的拟合估计结果比较

Figure 3. Comparison diagram of model inspection

图3. 模型检验比较图

对于其他州的能源演变规律，我们用相同方法可以求得，在此不再重复。

4. 总结

CA州所使用的能源基本全为石油与天然气，其中是有的消耗量更高，且明显高于其余能量的消耗总量，煤炭与进口电力的消耗量极少，州间销售电力及相关损失逐年增加，并且可再生能源的消耗量自1960年逐年增长。我们建议，CA州加强对可再生能源的生产，保证能源使用的清洁高效。

AZ州PMTCB、CLTCB、NUETB、NNTCB的数量演变规律基本一致，呈逐年增加趋势，其中石油的消耗量相对高些。其ELNIB的数量保持在很小的范围内波动，变化趋势不明显，说明AZ州净进口用电量较少。而其州间销售电力为负数且曲线向下增加，表明AZ州进口电力逐年增加。我们建议AZ州加强核电技术，用以提供本州所需电力，减少进口，同时继续发展清洁可再生能源。

NM州的天然气消耗量一直保持高水平不变，石油与煤炭的消耗量逐年增加，其中煤炭的增长速度更快，其进口电力始终保持低水平，对于可再生能源的消耗在2000年以后出现增长，进口电力相对其他州较多。我们建议，NM州以可再生能源的核电的使用量为主要目标，大力发展清洁能源，加强与其他轴之间的联系，以实现经济双赢。

TX州PMTCB与NNTCB的数量明显高于其他能源的消耗量，1980年以来煤炭的消耗量持续增加，其余四种能源消耗量水平较低，但初年增长的趋势。我们建议，TX州以核电为主要目标，加强清洁可持续能源的开发利用。