1. 前言
混凝土框架、框剪和框筒结构设计中,通常选用矩形截面柱(含方柱,以下简称矩形柱)或圆形截面柱,但为满足建筑外观、局部构造或使用功能需求,选用异形(非矩形与圆形)截面框架柱(以下简称异形柱)的情况屡见不鲜。相对矩形柱,求解异形柱(含通常所谓“墙柱”)的组合内力与各类配筋较复杂。目前设计软件进行整体结构计算分析时,绝大多数情况下,虽可积分解出其中异形柱的组合内力,并计入异形柱对结构空间性能的影响,但随后分解其截面为多个相互叠加的独立单元、分别按不同矩形截面计算配筋,不完全符合异形柱全截面协调变形的工作机理,使各单元截面的重叠部分不合理重复配筋,导致输出的异形柱计算配筋存在较大的不确定性。此外整体结构建模分析时,目前仍有部分特殊异形柱的截面信息难以准确输入。
为探索解决目前结构设计软件存在多年的上述问题,基于截面和双向弯曲惯性矩等效原则,本文系统提出了混凝土结构中异形柱原位代换为矩形柱的配筋方法,列出了任意异形截面代换为矩形截面的边长统一计算式,及常见异形截面代换为矩形截面边长的解析式,进行了相应技术分析与应用说明,并给出了相关设计建议,可作为现有结构设计软件计算异形柱配筋的补充方法。
矩形柱代换条件如下:异形柱沿其高度等截面,且各截面构造满足规范 [1] 、规程 [2] 要求;代换矩形截面形心位置同异形柱,过截面形心的两个正交方向(同结构平面直角坐标系)轴线无偏转;代换矩形柱的材料强度、两端约束条件、计算长度、截面面积与弯曲惯性矩均同异形柱。
为配合异形柱代换为矩形柱进行配筋,设计软件准确解出异形柱的组合内力后,随之求出其代换矩形截面边长,然后按代换矩形截面计算异形柱配筋。对于某些难以准确输入结构模型的特殊截面异形柱,亦可直接代换为矩形柱后输入结构模型计算组合内力及各类配筋。
2. 代换矩形截面边长
设任意截面异形柱的截面积
由有限n个规则单元面积
组成,正交x、y两轴的交点位于
形心处,绕x、y两轴的
的弯曲惯性矩分别为
、
,
的弯曲惯性矩分别为
、
,
的形心与x、y轴的间距分别为
、
,代换矩形柱的截面边长分别为
、
,可列出
(1)
(2-1)
(2-2)
联立式(1)、(2-2)及式(1)、(2-1)可分别解出
(3-1)
(3-2)
由式(3-1)、(3-2)确定的
、
,是任一异形柱基于截面积与x、y两向弯曲惯性矩等效的代换矩形截面边长的解析计算值。
时,有
,
、
分别为代换方形截面混凝土框架柱(以下简称代换方柱)的截面弯曲惯性矩与截面边长。
3. 部分代换矩形截面边长
时,工程中常见7种可代换为矩形柱的异形柱截面如图1,相应的
、
解析式分别如下。
3.1. T形截面
对于图1(a)所示T形截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
(4)
(5-1)
(5-2)
式中B、C、d、h、y1、y2分别为T形截面的翼缘宽度、腹板宽度、翼缘高度、腹板高度、形心距翼缘顶
边和腹板底边的距离,基于式(3-1)、(3-2)可分别解出
,
。

Figure 1. Common special-shaped sections of reinforced concrete columns (1)
图1. 常见异形混凝土柱截面(一)
3.2. 工形截面
对于图1(b)所示工形截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
(6)
(7-1)
(7-2)
式中B、C、H、d、h分别为工形截面的翼缘宽度、腹板厚度、截面高度、翼缘高度、腹板高度,基于式
(3-1)、(3-2)可分别解出
,
。
3.3. 十字形截面
对于图1(c)所示十字形截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
(8)
(9-1)
(9-2)
式中B、C、H、d分别为十字形截面的横板宽度、竖板宽度、竖板高度、横板厚度,基于式(3-1)、(3-2)
可分别解出
,
。
3.4. Π形截面
对于图1(d)所示Π形截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
(10)
(11-1)
(11-2)
式中B、C、H、d、h、x1分别为Π形截面的横板宽度、竖板宽度、竖板高度、横板厚度、横板净距、形
心与竖板外边缘间距,基于式(3-1)、(3-2)可分别解出
,
。
3.5. 椭圆形截面
对于图1(e)所示椭圆形截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
(12)
(13-1)
(13-2)
式中b、h分别为椭圆形截面的短轴宽度与长轴高度,基于式(3-1)、(3-2)可分别解出
,
。
3.6. 偏转矩形截面
对于图1(f)所示偏转矩形截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
(14)
(15-1)
(15-2)
式中b、h分别为偏转矩形截面的短边与长边,
为逆时针转角,基于式(3-1)、(3-2)可分别解出
,
。
3.7. 双肢矩形截面
对于图1(g)所示双肢矩形截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
(16)
(17-1)
(17-2)
式中b、h、
分别为双肢矩形截面的肢宽、高度、两肢间净距离,基于式(3-1)、(3-2)可分别解出
,
。
4. 部分代换方形截面边长
时,常见5种可代换为方柱的异形柱截面如图2,相应的
解析式如下。

Figure 2. Common special-shaped sections of reinforced concrete columns (2)
图2. 常见异形混凝土柱截面(二)
4.1. 正六角形截面
对于图2(a)所示正六角形截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
(18)
(19)
式中
为正六角形柱截面两侧平行边的间距,基于式(3-1)、(3-2)可解出
。
4.2. 正八角形截面
对于图2(b)所示正八角截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
(20)
(21)
式中
为正八角形柱截面两侧平行边的间距,基于式(3-1)、(3-2)可解出
。
4.3. 圆环形截面
对于图2(c)所示圆环形截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
(22)
(23)
式中
、
分别为圆环形截面的外径与内径,基于式(3-1)、(3-2)可解出
。
4.4. 方环形截面
对于图2(d)所示方环形截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
(24)
(25)
式中
、
分别为方环形截面的外边长与内边长,基于式(3-1)、(3-2)可解出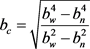 。
。
4.5. 外方内圆空心形截面
对于图2(e)所示外方内圆空心形截面混凝土柱,基于式(1)、(2-1)、(2-2)可列出 [3]
 (26)
(26)
 (27)
(27)
式中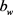 、
、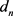 分别为外方形边长与内圆形直径,基于式(3-1)、(3-2)可解出
分别为外方形边长与内圆形直径,基于式(3-1)、(3-2)可解出 。
。
相对图2偏转的正六角形、正八角形、方环形、外方内圆空心形异形柱截面,见图3,其代换方柱的截面边长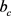 分别同3.1节、3.2节、3.4节、3.5节相应计算结果 [3] 。
分别同3.1节、3.2节、3.4节、3.5节相应计算结果 [3] 。
5. 截面配筋
结构分析计算确定异形柱的组合内力后,按代换矩形柱解出截面四周受力纵筋及其总面积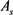 。异形柱截面纵筋总量取
。异形柱截面纵筋总量取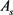 ,异形柱截面各受拉区的实配纵筋按照代换矩形截面相应部位计算配筋确定。
,异形柱截面各受拉区的实配纵筋按照代换矩形截面相应部位计算配筋确定。
参照文献 [4] ,异形柱各肢截面的长短边比值明显大于3时,用代换矩形截面确定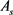 后,配筋构造还应满足对混凝土短肢剪力墙的相关要求。
后,配筋构造还应满足对混凝土短肢剪力墙的相关要求。
根据实际工程试算比较,异形柱箍筋的截面与间距可取代换矩形柱的相应计算值,但箍筋的设计位置、加工外形与下料长度应根据异形柱截面特征确定。
异形柱的纵筋和箍筋根据代换矩形柱计算确定后,其他各项(含柱端节点)构造措施还应满足文献 [1] [2] 的相关要求。
6. 截面构造
依据文献 [2] ,异形柱截面的肢厚不应小于200 mm,肢高不应小于500 mm;异形柱的剪跨比宜大于2,抗震设计时不应小于1.5。
依据文献 [1] [2] ,相对于抗震等级,代换矩形柱截面边长:四级或柱所在结构不超过2层时不宜小于300 mm;一至三级且柱所在结构超过2层时不宜小于400 mm;长短边比值不宜大于3。
注:如果代换矩形柱的截面长短边比值明显大于3,所对应的异形柱宜调整设计截面,或按混凝土剪力墙进行设计。
7. 分析与说明
理论上,根据变量 、
、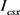 和
和 ,由式(1)、(2-1)、(2-2)可解出任意截面形状(全高等截面)异形柱的等效代换矩形截面边长
,由式(1)、(2-1)、(2-2)可解出任意截面形状(全高等截面)异形柱的等效代换矩形截面边长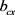 、
、 ,因此上述异形柱代换为矩形柱的配筋方法有较好的适用性。
,因此上述异形柱代换为矩形柱的配筋方法有较好的适用性。
由于代换矩形截面边长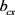 、
、 或
或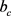 均程度不同小于异形柱截面的同向最大长度,使代换矩形截面受拉纵筋合力的计算力臂略小于实际值,导致
均程度不同小于异形柱截面的同向最大长度,使代换矩形截面受拉纵筋合力的计算力臂略小于实际值,导致 稍大于文献 [1] [2] 的相应计算值,使按本文方法确定的异形柱受弯承载力偏于安全。
稍大于文献 [1] [2] 的相应计算值,使按本文方法确定的异形柱受弯承载力偏于安全。
在可比条件下,由代换矩形柱计算确定的异形柱截面一侧受拉纵筋面积与数值积分解出的相应值之比(≥1.0),等同异形柱与代换矩形柱同侧纵筋力臂的比值。柱截面一侧多排纵筋的力臂长度,可根据该侧纵筋的合力点位置计算确定。

Figure 3. Common special-shaped sections of reinforced concrete columns (3)
图3. 常见异形混凝土柱截面(三)
环形等空心截面异形柱(参见图2)用代换矩形截面柱确定配筋后,为确保实现“强柱弱梁”、“强节点弱杆件”的抗震设计目标,这些柱的上下两端应设计调整为实心截面柱段,且段长不宜小于 或
或 。
。
上述“等效代换”仅限代换矩形截面的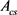 、
、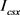 和
和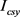 同相应异形柱,而代换矩形柱的扭转惯性矩可能稍小于相应异形柱。因此代换矩形柱的组合内力宜先取结构分析确定的相应异形柱的准确值,然后按代换矩形截面计算配筋。仅当异形柱输入结构模型受限,且可忽略扭转惯性矩的非等效对组合内力计算精度的影响时,可直接将代换矩形柱输入结构模型计算异性柱的组合内力和各类配筋。
同相应异形柱,而代换矩形柱的扭转惯性矩可能稍小于相应异形柱。因此代换矩形柱的组合内力宜先取结构分析确定的相应异形柱的准确值,然后按代换矩形截面计算配筋。仅当异形柱输入结构模型受限,且可忽略扭转惯性矩的非等效对组合内力计算精度的影响时,可直接将代换矩形柱输入结构模型计算异性柱的组合内力和各类配筋。
如果代换矩形柱的扭转惯性矩小于相应异形柱,可能使代换矩形截面的组合扭矩略偏小、异形柱的计算箍筋稍偏少。但由于代换矩形截面的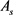 值偏大,经试算比较,可借此补偿异形柱因箍筋偏少而损失的截面受扭承载力。根据偏压混凝土异形柱设计经验、计算研究与相关文献 [5] [6] [7] ,在可比条件下,异形柱与相应代换矩形柱的组合内力与
值偏大,经试算比较,可借此补偿异形柱因箍筋偏少而损失的截面受扭承载力。根据偏压混凝土异形柱设计经验、计算研究与相关文献 [5] [6] [7] ,在可比条件下,异形柱与相应代换矩形柱的组合内力与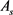 基本相同,工程中绝大多数情况下,异形柱计算箍筋均由截面抗剪承载力或规范构造要求、而非计算受扭承载力确定。
基本相同,工程中绝大多数情况下,异形柱计算箍筋均由截面抗剪承载力或规范构造要求、而非计算受扭承载力确定。
注:对于各类混凝土异形柱,箍筋满足构造要求后,不宜首选增加箍筋、应尽量增大截面以较快提高其受扭承载力。
结构设计时,异形柱的箍筋根据代换矩形柱相应计算值调整适宜外形、嵌套组合布置后,重叠箍肢与环箍内拉筋均有增加,使异形柱的受扭和受剪承载力相对代换矩形柱有所增大。
当结构设计所用软件难以或无法准确计算某些特殊异形柱的配筋时,可按本文方法代换矩形柱输入结构模型计算组合内力和各类配筋。此时如确需精确考虑实际异形柱与代换矩形柱的扭转惯性矩非等效的影响,可依据两者组合扭矩的比值,增大调整代换矩形柱的箍筋计算值。
8. 结论
1) 根据本文方法按代换矩形柱确定相应异形柱的配筋,可降低目前设计将异形柱截面分解为若干相互叠加的独立单元、分别按矩形截面计算配筋的不确定性,计算精度满足工程要求,且总体上偏于安全。
2) 异形柱宜根据整体结构模型计算分析确定组合内力,然后按代换矩形柱计算各类配筋。对某些特殊情况或软件功能受限时,可直接按代换矩形柱确定异形柱的组合内力和各类配筋。
3) 任意截面异形柱代换为矩形柱时,矩形截面边长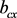 、
、 由解析式(3-1)、(3-2)计算确定。
由解析式(3-1)、(3-2)计算确定。
4) 异形柱代换为矩形柱前后,其截面构造需先满足现行相关规范、规程的相应要求。