有力筋块体自由摇摆振动恢复系数有限元分析

FEM Analysis of Restitution Coefficient of Free Rocking Block with Tendon

摘要: 采用ABAQUS数值模拟方法，建立了有力筋块体自由摇摆振动的数值模型，以块体的高宽比、力筋刚度、初始位移为分析参数，研究了不同参数水平下块体自由摇摆振动的恢复系数。研究发现恢复系数具有一定的随机离散性；高宽比对恢复系数有显著影响，力筋的施加以及初始位移的大小对恢复系数几乎没有影响；恢复系数的理论值，可以直接用于高瘦型块体的计算，但对矮胖型块体的计算则误差较大。给出了不同情况下恢复系数的试验平均值，可供计算时参考。

Abstract: The values of coefficient of restitution (COR) of free rocking blocks with tendons were investigated by establishing numerical models using ABAQUS. The analysis parameters were the aspect ratio, tendon stiffness, and initial displacement. The results reveal that the COR showed some random nature. The aspect ratio had a significant effect on the COR, however the tendon stiffness and the initial displacement had little effect on the COR. The theoretical COR formula was accurate enough for slender blocks, but showed larger errors for dumpy blocks. The average values of COR for cases covered in this paper were given for reference use in related calculations.

1. 引言

目前，除了采用消震与隔震措施，一般的建筑结构在地震作用下是通过自身的不可恢复变形和损伤来耗散地震能量，在大震作用下，即使结构没有发生倒塌，因耗散地震能量而产生的变形和损伤也常常会导致结构难以修复或加固费用昂贵，甚至需要推倒重建。而摇摆结构在地震作用下以刚体运动为主，变形和损伤均很小，因此受到越来越多研究者的关注 [1] [2] [3] [4] 。

摇摆结构的概念由Housner [5] 于1963年首次提出。Housner以刚性地面上的平面矩形刚性块体(图1)作为研究对象，分析了块体在自由振动下的周期及耗能，在常水平加速度、正弦波加速度及水平地震力作用下的倾覆反应。Pena [6] 等通过试验研究了花岗岩块体在刚性基础上的自由振动摇摆响应，并采用两种计算模型分别计算块体在正弦波激励和地震波激励下的反应。Cheng [8] 用有力筋的钢筋混凝土试块模拟桥墩进行了自由振动试验，分析了接触面材料、力筋面积、试件高宽比及横截面尺寸四个影响因素对混凝土块体在摇摆振动中的滑移、最大加速度、阻尼比等响应的影响。Maryam [9] 等以NEESR-CR项目中的摇摆墙为原型，进行了四个1/3.6单片有力筋的摇摆墙试件的振动台试验，分析了初始预应力和力筋截面面积对墙体的底部应力、碰撞面范围及抬升高度的影响。Vassiliou和Makris [10] 从理论出发研究了有力筋块体(图2)在地震作用下的摇摆振动响应，分析了力筋的刚度对系统刚度的影响。

Schau [11] 等将摇摆振动理论方程所得位移响应与ABAQUS模拟结果进行了比较，其中方程计算采用四阶Runge-Kutta迭代法并采用不同的恢复系数分析；ABAQUS模拟中采用平面应力单元，分析不同的接触条件、基础特性、刚体底部几何尺寸的微小改变对位移响应的影响。Kalliontzis [12] [13] 等做了一系列摇摆振动试验，基于ABAQUS对试验进行模拟，并在模拟中引入Rayleigh阻尼系数，研究了摇摆振动过程中柱的位移时程、速度–位移相图以及力筋中力的变化图。

目前，虽然对摇摆振动已有一定的理论与试验研究，但理论研究基本都是基于块体和基础都为刚性且无弹跳与滑移的假定，同时相应的试验研究成果较少，如何建立合理有效的摇摆振动模型仍处于探索之中，各参数对振动响应的影响也有待进一步分析与讨论。

本文提出一种模拟摇摆振动的ABAQUS建模方法，通过与已有试验结果对比验证方法的正确性。模型根据实际情况定义材料特性和接触特性，避免了理论研究的刚体假定和无弹跳、滑移的假定，之后研究了不同参数水平下块体的碰撞恢复系数。

2. 有限元模型的建立与验证

2.1. 试验说明

本文以Kalliontzis [13] 完成的摇摆振动试验作为标定试验，验证建模方法的正确性。试验中的摇摆系统(图3)主要由柱、基础、柱顶质量块、水泥层以及柱内无粘结力筋组成，各部分尺寸如图3所示。柱的质量为553.4 kg，质量块重1080 kg，质量块顶部与柱顶齐平；力筋两端分别与柱顶面和基础底面锚固。力筋采用强度等级为Grade270的七束钢绞线，横截面面积为140 mm²，初始预应力为69.9 MPa，弹性模量为199,948 MPa。柱、质量块、基础的弹性模量为26,372.45 MPa，水泥层为41,368.55 MPa。试验中，液压千斤顶通过牵拉环在质量块的高度中部施加力，使柱产生初始角位移0.03 rad，之后释放该力，使柱体产生自由摇摆振动，并通过LED测控系统测量位移。

Figure 1. A rocking block [5]

图1. 摇摆块体 [5]

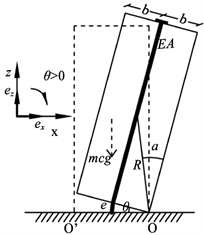
Figure 2. A rocking block with tendons [10]

图2. 有力筋的摇摆块体 [10]

Figure 3. The experiment rocking system (unit: m)

图3. 试验中的摇摆系统(单位：m)

Figure 4. The ABAQUS model of the experiment rocking system

图4. 试验中摇摆系统的ABAQUS模型

2.2. ABAQUS有限元模型说明

对摇摆振动选用显式动力学方法建立接触条件更为容易，因此选用ABAQUS 6.13/Explicit作为分析平台。模型中各部分尺寸及材料参数按照试验取定，材料为弹性，力筋线膨胀系数根据钢结构设计规范取1.2 × 10⁻⁵。完成的ABAQUS模型如图4所示，对建模中关键内容说明如下。

2.2.1. 网格划分及单元类型选取

在系统摇摆过程中，整体以刚体运动为主，只有柱底部与水泥层有碰撞，为减小模型的体量，将柱沿高度方向分段划分网格。上部和下部采用C3D8R单元，增强沙漏控制(enhanced)，中间过渡部分选择C3D4单元。力筋选用T3D2，基础、质量块、水泥层以及锚板的单元类型与柱上部相同。

2.2.2. 各部件之间相互作用定义

柱与质量块、基础与水泥层分别以一个部件建模；柱顶部和锚板、基础底部和锚板之间用束缚约束(Tie)连接在一起。以柱底面和水泥层顶面作为接触面定义通用接触，切向特性中摩擦公式选罚函数(Penalty)，摩擦系数取0.6，法向特性中选硬接触(“Hard” Contact)，其余取默认值。

2.2.3. 分析步的设置及荷载、边界条件施加

试验通过五个分析步来实现。初始分析步，加z向重力g = −9.8 m/s²，约束基础底面三个方向的平动位移。第二个分析步，以降温法给力筋施加初始预应力，分析步时长0.01 s。第三个分析步，给柱体及质量块施加绕y轴初始角位移0.03 rad，时长0.2 s；为防止出现三维振动，约束柱体和质量块的y向平动位移直至分析结束。第四个分析步，使柱体及质量块在初始位移状态下保持稳定，时长0.05 s。第五个分析步，释放初始位移，使结构摇摆，时长5 s。

2.3. 有限元结果与试验结果对比

2.3.1. 数值计算有效性分析

在ABAQUS/Explicit分析中，可以通过各种能量之间的比较，帮助评估一个分析是否得到了合理及准确的响应(ABAQUS 6.13帮助文件)，通常总能量(total energy, ETOTAL)应保持为一个常数或接近于一个常数，伪应变能(artificial energy, ALLAE)与实际的能量如动能(kinetic energy, ALLKE)、内能(internal energy, ALLIE)相比应是可以忽略的。图5给出摇摆过程中的能量图，可以看到，总能量的数值基本保持在2~5之内，伪应变能接近于零，与动能和内能相比，总能量接近于一个常数，伪应变能可以忽略，因此认为模型结果计算有效。

2.3.2. 位移时程对比及分析

通过GetData Graph Digitizer软件对试验结果(文献 [13] 中的Figure 4-18)进行数据提取，试验与数值模拟所得的角位移时程对比结果见图6。

由图6可以看到，在振动前4 s，试验结果与数值模拟所得结果在振动周期上吻合度很好，振幅间的差值随着振动时间的增加逐渐增加。造成振幅有差值的原因主要是数值模拟中没有考虑力筋与管道之间的摩擦产生的能量损失。实际试验中，力筋与管道之间不可避免的存在着摩擦，在结构摇摆的过程中，力筋反复伸长与回缩，与管道之间产生摩擦进而产生能量损耗，导致振幅减小。由于目前的建模方法还不能准确的模拟这部分耗能对振幅的影响，同时考虑到本文主要探讨不同参数对恢复系数的影响，因而本文数值试验中均不考虑此项摩擦。

3. 有无力筋时碰撞恢复系数的有限元试验设计

3.1. 数值试验模型

图7为有力筋块体摇摆振动的计算简图。块体以角点O或O’为转动轴作刚体运动，当块体运动到 $\theta =0$ 时，与基础发生碰撞，随之转动轴发生改变，因而摇摆振动的方程是分段连续的。根据块体绕角点O的动量平衡推导得到块体绕一个角点的运动方程如式(1)：

$I_O\frac{{\text{d}}^2\theta }{\text{d}{t}^2}\text{+}WR\sin \left(\alpha -\theta \right)\text{+}\left(F_0+F_e\right)b=0$ (1)

式中 $I_O=4{\text{MR}}^2/3$ 是矩形块体对角点O的动量矩，W是块体重力， $F_e=E_s{A}_s\epsilon =E_s{A}_s\tan \alpha \left|\sin \theta /2\right|$ 是由力筋伸长产生的恢复力， $F_0={\sigma }_0{A}_s$ 是由初始预应力产生的恢复力。由(1)式可以看到，在振动过程中，有力

Figure 5. The energy in the system

图5. 系统能量图

Figure 6. Comparison of angular displacement time histories

图6. 角位移时程对比图

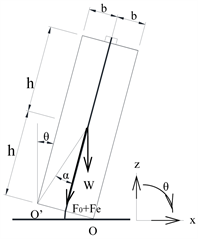
Figure7. A rocking block with tendons

图7. 有力筋块体计算简图

筋的块体有三部分恢复力，W、 $F_e$ 及 $F_0$ ，当 $F_0=0$ 和 $F_e=0$ 同时满足时，(1)式即为无力筋的摇摆振动系统的运动方程，只有重力恢复力，同Housner [5] 提出的运动方程一样。

理论方程中一般假定能量损耗集中在碰撞过程，并以Housner [5] 提出的恢复系数r来表示能量损耗。当r值已知，则摇摆振动的整个运动过程即确定，因此r在摇摆振动的研究中有极为重要的作用。r定义为碰撞后与碰撞前块体的动能之比，对矩形无力筋的块体 $r={\left(1-3{\sin }^2\alpha /2\right)}^2$ ，目前关于恢复系数的研究 [6] [7] [14] 仍是基于试验在此基础上进行修正，并没有统一有效的方法可以直接计算恢复系数，而对有力筋块体的恢复系数目前还没有相关计算公式。

3.2. 试验说明

数值试验模型包括块体、基础、力筋及锚板(图8)。基础和块体的材料选C30混凝土，弹性模量为3 × 10¹⁰ Pa，密度为2400 kg/m³。块体与基础间的摩擦系数取0.6。所有模型中的基础尺寸均为1.5 m × 1.5 m × 0.4 m (长 × 宽 × 高)。力筋采用钢绞线，弹性模量为1.95 × 10¹¹ Pa，密度为7850 kg/m³，线膨胀系数 $\alpha =1.2\times {10}^{-5}/℃$ ；锚板选用钢板，弹性模量2.06 × 10¹¹ Pa，密度7850 kg/m³。为防止三维振动，约束块体y方向中面(即ABC面)的y向位

根据定义，恢复系数由碰撞后与碰移，分析步设置、边界条件以及荷载施加方式都与标定试验相同。

定义力筋刚度为 ${\prod }_E=E_s{A}_s/W$ ，角位移为 $\Theta \text{=}\theta /\alpha$ ，数值试验中取块体宽度为0.4 m，初始预应力为0，以块体高宽比h/b、力筋刚度 ${\prod }_E$ 及初始角位移 ${\Theta }_0$ 为变量设计了具有不同水平的12个数值模型(见表1)，可以看到，这三个参数均是无量纲参数，当 ${\prod }_E\text{=}0$ 时即为无力筋的情况。模型名称按照“h/b- ${\prod }_E$ - ${\Theta }_0$ ”的方式编写，如4-300-0.1表示块体高宽比为4，力筋刚度 ${\prod }_E\text{=}300$ ，初始角位移 ${\Theta }_0\text{=0}\text{.1}$ 。

4. 试验结果及分析

撞前的动能之比求得，在本文计算中，由于在摇摆过程中块体无明显损伤，故认为块体质量在整个摇摆过程中保持不变，由碰撞后与碰撞前速度的平方之比求得各数值模型的恢复系数。图9(a)~图9(d)给出了12个数值试验的恢复系数随碰撞次数n的变化图，图中实线为恢复系数理论值(以下简称理论值)，高宽比为4、6、10时，理论值分别为0.83132、0.92056、0.97052。

由图9可以看到，因为考虑了块体和基础的实际材质以及接触条件，数值试验所得的恢复系数(以下简称试验值)并不是一个固定值，而是在振动过程中以理论值为基准线随机波动，整体呈现离散状态，由文献 [14] 也可看到这一点。高宽比为6和10的块体，恢复系数的离散性较小，且高宽比为6的块体其理论值是试验值的下限，而高宽比为10的块体其理论值则基本是试验值的均值，相比较而言，高宽比为4的块体的恢复系数离散性更大，理论值是试验值的偏上界。

对块体在整个振动过程中的恢复系数取平均值，并将试验平均值r₁与理论值r₀进行比较，以e = (r₁ − r₀)/r₀表示试验平均值与理论值的相对差值，见表2。

Table 1. Parameters of model specimens

表1. 模型试件参数

Table 2. Average values of COR

表2. 恢复系数平均值

注：有力筋情况1包括4-300-0.1、6-300-0.1、10-650-0.1、6-70-0.5，有力筋情况2包括4-650-0.1、6-650-0.1、10-6500-0.1、6-300-0.5。

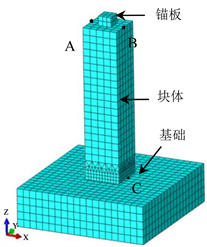
Figure 8. ABAQUS model used in the numerical analysis

图8. 数值分析的ABAQUS模型

Figure 9. The values of COR of model specimens

图9. 模型试件的恢复系数

从表2看，对高宽比为4的块体，力筋的施加对恢复系数r的平均值有较为明显的影响，但由图9(a)可以看到，因为r本身具有极大的离散性，所以实际的r并不因力筋的施加而具有显著变化；对高宽比为6和10的块体，无论是从表2中r的试验平均值方面还是图9(b)~图9(d)中r随碰撞次数变化方面，力筋的施加对恢复系数都不具有显著影响。由图9(b)、图9(d)以及表2可以看到，初始位移对恢复系数没有显著影响。

5. 结论

1) 在振动过程中，恢复系数r具有一定的随机离散性，并不像理论所得为一恒定值，且矮胖型块体的恢复系数离散性更大。

2) 对瘦高型的块体，其恢复系数可以用理论计算值表示，相对误差很小；但是对于矮胖型块体，理论值存在较大误差。本文给出的各工况下的恢复系数试验平均值，可供相关计算参考。

3) 块体是否加力筋以及所加力筋的大小，对恢复系数似无显著影响。

4) 初始位移的大小对恢复系数无明显影响。

本文的建模方法未考虑力筋与管道之间的摩擦，同时因为计算时间原因对高宽比为6和10的块体并未分析其运动全过程，只分析了前10 s的运动，之后的研究可以在这些方面进一步改进与探讨。

基金项目

国家自然科学基金项目(51178328)。

NOTES

^*通讯作者。