城市道路交通控制子区划分策略研究

Study on Sub-Area Division Strategy of Urban Road Traffic Control

摘要: 由于城市道路系统的复杂性、随机性、动态性等特点，对整个路网进行统一的交通诱导与控制显然是不现实的。因此要实现有效的交通诱导与控制，应该根据城市空间和功能的发展变化来对整个交通网络系统进行分区。本文从静态方法、动态方法阐述了交通控制子区划分的研究现状并指明其中存在的不足，给出了根据节点状态进行交通控制子区划分的原则，详细设计交通控制子区划分算法。最后运用标准测试网络Sioux Falls网络对划分算法进行验证。实例分析表明，该算法能够实现有效的交通诱导与控制，缓解交通拥堵。

Abstract: Because of the complexity, randomness and dynamics of the urban road system, it is obviously unrealistic to unify the traffic guidance and control of the whole road network. Therefore, in order to achieve effective traffic guidance and control, the whole traffic network system should be zoned according to the development of urban space and function. The paper expounds the present research situation of traffic control sub-area division by static and dynamic methods and points out the shortcomings, gives the principle of dividing the traffic control sub-area according to the node state, and designs traffic control cell partition algorithm in detail. Finally, the standard test network Sioux Falls network is used to verify the partitioning algorithm. Case analysis shows that the algorithm can achieve effective traffic guidance and control, and alleviate traffic congestion.

1. 引言

随着汽车保有量的急剧增加，在大城市尤其是特大城市对几百个甚至上千个交叉口的路网进行信号控制时，经常将路网划分成多个相互独立的区域，每个区域包含1个或者相邻的多个交叉口，即交通控制子区。当控制子区从出行活动性质、行政区域功能、地形地貌等方面考虑时，子区在长时间段内是无变化的。在城市交通诱导与控制领域，由于交通流状态变化具有复杂性、随机性和动态性，所以将整个路网分解成多个交通控制子区进行分别诱导与控制是当今社会发展的必然趋势。SCOOT和SCATS系统作为非常典型的城市交通控制系统，从控制子区的角度出发建立交通模型，进而对路网进行整体优化，取得了较好的成果。

1971年，美国学者Walinchus首次给出交通控制小区的定义 [1] 。Yagoda等学者从数学建模的角度考虑，对子区划分的控制指标、控制阈值和划分算法进行了深入研究，但最后并没有得出具体的子区划分方法 [2] 。由于早期的子区划分方法一般使用静态方法划分，以路网的物理特征作为划分依据，所以不能适应目前复杂的动态交通变化需求。为了找到与目前复杂交通系统中交通诱导与控制相匹配的子区划分方法，于是开始着眼于动态角度研究。王学堂把区域复杂系统分解为几个简单系统，对各个子系统进行研究 [3] 。高云峰、杨晓光等主要考虑物理关联和路径关联等原则，对交叉口群的划分方法进行了研究，把交叉口间的关联性作为划分交叉口群的依据 [4] 。这些子区划分方法的是基于常态条件下的交通控制，对非常态交通条件下的交通控制子区的划分方法并没有深入研究。除此以外，王薇还从诱导角度出发，讨论了基于网络平衡的大范围交通流动态管理，她提到为解决计算效率瓶颈问题，应对路网进行有效划分，提出了在路网诱导层面划分诱导子区的解决思路 [5] 。

上述交通控制子区的划分方法，有些只是给出了划分的原则，没有给出具体的计算步骤，有些是静态方法，虽然相对较为简单，计算量不大，但考虑到交通状态的瞬息万变，这些方法在复杂的城市交通系统中不实用。有些方法虽然是动态计算的，但没有考虑到针对区域交通状态进行量化分析，没有建立不同路口、路段的状态连通矩阵，因此交通控制小区的划分也有一定的局限性。

2. 交通控制子区划分原则

交通控制的路口节点虽地域范围小，但却是交通瓶颈，直接影响道路状态，是控制策略实施的主要场所，因此根据节点状态进行交通控制子区划分。交通状态是时空连续变量，控制子区也是动态划分的。交通优化控制的目标在于最大程度地发挥交通系统的作用，将车辆尽量均衡分布在所有路口和路段上，避免局部拥挤，因此交通拥挤的路口群成为控制实施的重点。为保证控制子区内各路口间能够协调控制，疏导拥挤交通流，将拥挤区域与邻近稀疏路口划为同一子区，便于路口间信号协同配时 [6] 。

基于上述思想，划分原则如下：

1) 中心关键–周边疏通原则

以可达值最低的一个或几个相邻路口为关键节点，紧邻的周边路口为疏通节点，划为一个控制子区；

2) 拥挤低谷点作边界原则

以两个子区节点的集合中，可达值最大的点为控制子区边界，边界的低谷点为中心的关键路口服务，类似原理如图1所示；

3) 交通状态相似原则

根据城市规模等级，在一定的道路拥挤度 $\lambda$ 下，若两相邻路口的状态连通值为0，则该两节点划为同一子区集合；

4) 距离范围为上限原则

考虑到路口距离较远时，实施信号相位协同效果不明显，因此子区集合内的节点限定在直线方向上1000米范围内。

3. 交通控制子区划分算法

根据上述原则，设计在某考察时刻交通控制子区划分算法，为表达方便，绘制算法流程分为两个部分，主算法流程如图2所示，子算法流程如图3所示。具体算法过程如下：

Step 1：初始化：建立集合M，元素为所有路段交叉口节点；建立若干集合Mi，设置为空集，算法结束后M_i为第i个小区的节点集合；设s = 0；

Step 2：计算所有节点 $j\left(j=1\cdots m,j\in N\right)$ 的可达值 $Q\left(i\right)$ ，所有链路 $l_{ij}$ 的路段交通状态系数；

Step 3：新建集合T，将所有 $Q\left(i\right)$ 按照从小到大排序，并依序置入集合T；

Step 4：从T中依序取出 $Q\left(i\right)$ ，进行以下操作：

1) 判断是否满足 $C_{ij}\left({\lambda }_{\tau }\right)=0$ 且 $c_{ij}\left({\lambda }_{\tau }\right)=0$ ，若不满足，结束Step 4，否则转(2)；

2) 判断是否满足 $i\in M,j\in M$ ，若不满足，转(3)，否则：节点 $i$ ， $j$ 置入新建集合 $Ms$ 中，同时从集合M中删除，即 $s=s+1,Ms=\left\{i,j\right\},M=M-\left\{i,j\right\}$ ；并结束Step 4；

3) 判断是否满足 $i\in M,j\in Mq$ ，若满足，转(4)，否则，转(6)；

4) 判断若节点i加入到结合 $Mq$ ，则 $Mq$ 最大跨距是否大于1000米，若是，则转(5)，否则结束Step 4；

5) 判断是否满足 $p_i>p_k,\forall k\in Mq$ ，若满足，则节点i加入到集合 $Mq$ ，集合M中删除节点i；否则， $s=s+1,Ms=\left\{i,j\right\},Mq=Mq-\left\{j\right\}$ ；完成后结束Step 4；

6) 判断是否满足 $i\in M_a,j\in M_b$ ，若是，转(7)，否则，结束Step 4；

7) 判断若 $M_a$ 与 $M_b$ 合并，合并后最大跨距是否小于1000米，若是则转(8)，否则结束Step 4；

8) 判断对任意 $x\in M_a,y\in M_b$ ，是否有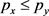成立，若是，则 $M_a=M_a\cup M_b$ ，结束Step 4；否则，转(9)；

9) 排序比较，确定 $M_a$ 中关键路口 $c_a$ ， $M_b$ 中关键路口 $c_b$ ；判断 $c_a$ 与 $c_b$ 的距离是否小于1000米，若是则转(10)，否则结束Step 4；

10) 判断是否满足 $p_a<p_b$ ，若是，则 $M_b=M_a\cup M_b$ ，否则 $M_a=M_a\cup M_b$ 。

Step 5：判断集合T是否清空，若是，转Step 6，否则转Step 4；

Step 6：对M中剩余的每个元素i，进行操作：新建集合 $M_s$ ，将i置入 $M_s$ ，同时从M中删除节点i，即 $s=s+1,M_s=\left\{i\right\},M=M-\left\{i\right\}$ ；

Step 7：算法结束。

算法中集合的最大跨距，表示集合中的所有节点，在任意方向上的最远距离。集合中的节点，取通行度最小的节点作为关键路口。

Figure 1. Graph of peak-trough

图1. 峰值–低谷示意图

Figure 2. Control subarea division main algorithm flow

图2. 控制子区划分主算法流程

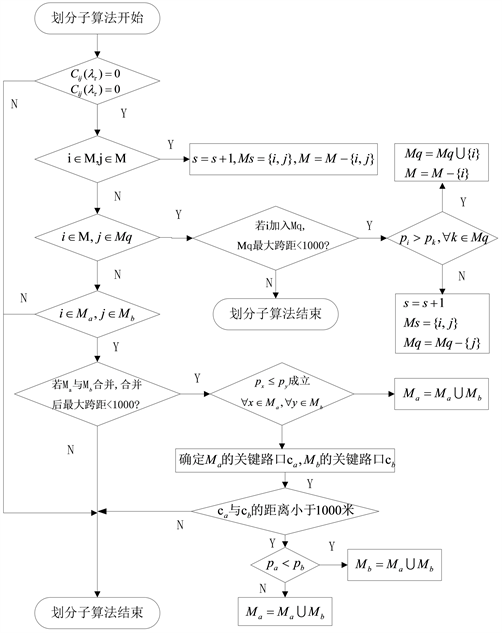
Figure 3. Control subarea division sub-algorithms flow

图3. 控制子区划分子算法流程

4. 实例分析

为验证上述模型和算法，本文对通用的标准测试网络Sioux Falls网络进行优化计算，运算结束将结果以图形化输出。

图4中圆圈代表交叉口，相邻交叉口有路段连通，共24个路口，74条路段，路段长度与图中等比放大，设置为双向六车道。表1中给出了具体产生交通需求的路段及平峰(饱和度为0.6)与高峰期(饱和度为1.2)时的路段交通需求量，表2给出了各路段的通行能力，表3给出了各路段的长度表示。路段行程时间用通用的交通阻抗表示：

$t_a\left(x\right)=t_{a0}\left[1+\alpha {\left(\frac{x_a}{C_a}\right)}^{\beta }\right]$

上式中， $t_{a0}$ 为路段a的自由行程时间， $x_a$ 、 $C_a$ 分别为路段a的交通需求和通行能力，参数 $\alpha$ 、 $\beta$ 分别取0.15和4。根据行程时间和路段长度，可求出路段平均行驶速度。计算节点的通行度时，利用4个交通拥挤程度截值依次计算各路口节点的通行度。

图5、图6分别给出了交通饱和度分别是0.6、1.0的情况下，控制子区的划分情况。从图中可看出，在交通畅通时，流量小，各路口之间相互影响不大，一般2~3个路口构成小区，甚至单个路口独立分区。但在交通过饱和时，拥堵路口增多，同时为疏通拥挤路口车流，多个附近畅通路口与拥挤路口协同，单个控制小区规模扩大，数量减少。表3给出了所有节点的通行度和子区划分情况。

Figure 4. An example of a road network based on Sioux Falls

图4. 基于Sioux Falls的路网实例

Figure 5. Traffic control subarea division with a saturation of 0.6

图5. 饱和度为0.6的交通控制子区划分

Table 1. Traffic requirements under different conditions

表1. 不同状态下的交通需求

Table 2. Correlation parameter values of sections in Sioux Falls network

表2. Sioux Falls网络中各路段的相关参数值

Table 3. Section length

表3. 路段长度

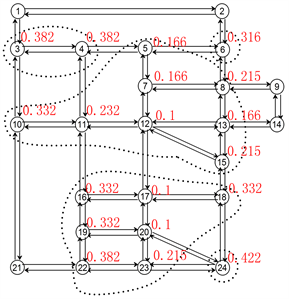
Figure 6. Traffic control subarea division with a saturation of 1.0

图6. 饱和度为1.0的交通控制子区划分

5. 结论

本文针对目前交通控制子区划分的不足之处，考虑到针对区域交通状态量化分析，建立不同路口、路段的状态连通矩阵，通过建立控制子区划分算法和模型，实现了城市道路交通控制子区的动态划分。最后对通用的标准测试网络Sioux Falls网络进行优化计算，给出不同饱和度时的控制子区划分情况。结果表明，该策略能够较好的对交通控制子区进行划分，比目前的子区划分效果提高一倍。

基金项目

山东省自然科学基金项目“基于车载互联的多尺度路网状态辨识与诱导控制研究”(ZR2012FL02)山东省高等学校科技计划项目“道路交通系统的粗糙集模型与控制方法研究”(J10LG52)。

NOTES

^*通讯作者。