1. 引言
完整的晶体中的原子,由于周期性的排列,使晶体中运动的电子具有能带结构。由介质周期性排列形成的光子晶体对光的作用,类似于晶体对电子的作用,也让光在光子晶体中传播时,在一些波长范围内能够透射,而在另外的波长范围内不能透射。把不能透射的波长范围(也可以折算成对应的能量范围)叫带隙。光子晶体由于其优异的性能,成为光子学、光电材料研究的热门领域 [1] [2] 。研究光在光子晶体中传播性质的方法有平面波展开法,转移矩阵法,有限时域差分法(Finite Difference Time Domain,简称FDTD)。二维光子晶体是由介质柱在平面内周期性排列,在第三维无限延长构成的结构,它相对于三维光子晶体,计算量比较小,便于研究。如何利用二维光子晶体获得多个宽的带隙,使光子晶体的带隙满足工程的需要,是一个令人感兴趣的问题。Xiao-Jing Liu综述了函数光子晶体的带隙性质 [3] ,D. R. Sollia,J. M. Hickmann 研究了带隙作为填充率和折射率函数的性质 [4] ,Xiao-Jing Liu,Jing-Bin Lu,Ji Ma,Zhi-Guo Wang a研究了折射率作为半径函数的光子晶体的带隙的性质 [5] [6] 。本文希望用两种不同的光子晶体获得比较大的带隙的光子晶体。
2. 光子晶体的带隙理论和有限时域差分法
FDTD方法,是由K. S. Yee在1966年提出的 [7] ,其基本思想是把数学中的微分用差分代替,用中心差分法表达导数为 [8] :
,
由于计算机的储存容量的限制,计算的物理区间是有限的,用FDTD方法计算时,被广泛使用的是完全匹配吸收层 [9] (PML),通过选择边界内的电导率和磁导率的比值:
,使电磁波从介质入射到边界后,被完全吸收,不被反射。
用FDTD方法推导的2维TE模式的电磁波递推表达式 [10] :
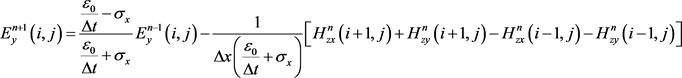 ;
;
;
;
;
在完全绝缘介质中,取
。
3. 由圆柱介质构成的二维光子晶体的透射谱
对于二维正方格子光子晶体的带隙已经有很多研究工作 [11] - [19] ,但是,不同结构的带隙的对比,以及三角形结构和六角形结构的带隙并没有系统的结果,下面分别进行研究。
3.1. 圆柱介质构成的正方形二维光子晶体的带隙
圆柱介质折射率分别设置为n = 1.5,1.8,2.5,介质柱半径设置为
,介质柱构成正方形结构。研究两种不同的结构:介质柱相切排列,晶格常数
;介质柱不相切排列,
,整个结构的背景介质是空气,等距离排列成
和
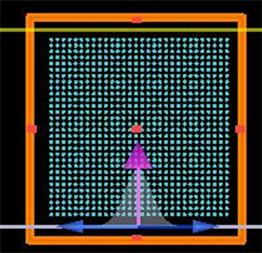
方阵,整个结构在Z方向没有长度,构成二维晶体。信号源是高斯型,波长范围设置为0.4~2.0 μm。使用PML边界,PML层数为14层,反射率0.0001。结构如图1:
 (1)
(1)
 (2)
(2)
Figure 1. The structure of (1):
and (2):
two-dimensional square photonic crystals and light source
图1. (1):
和(2):
方阵二维光子晶体的结构和光波源
光波穿过光子晶体,在检测的一条线上被接收,检测抽样频率点500,计算区域网格最小步长为
。
后面计算例子的PML层的参数、计算网格参数的设置与此相同,不再赘述。位于光源正前方的接收处,坡印廷矢量与波长之间的关系如图2所示。
把计算结果列为表1。

Figure 2. Transmission properties of (a)
and (b)
two-dimensional square photonic crystal to light waves
图2. (a)
和(b)
方阵二维光子晶体对光波的传播性质

Table 1. Transmission properties of two-dimensional square photonic crystals
表1. 二维正方形光子晶体的透射性质
最大带隙分别为0.30 μm和0.26 μm,已经在表中用黑体字表示。
3.2. 圆柱介质构成的三角形二维光子晶体的带隙
圆柱介质折射率分别设置为n = 1.5,1.8,2.5,介质柱半径设置为
,介质柱构成三角形结构。研究两种不同的结构:介质柱相切排列,晶格常数
;介质柱不相切排列,
,整个结构的背景介质是空气,等距离排列成
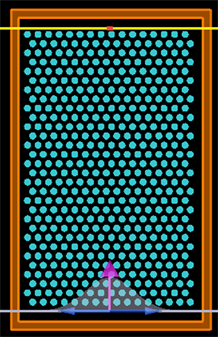
方阵,整个结构在Z方向没有长度,构成2维晶体。信号源是高斯型,波长范围设置为0.4~2.0 μm,使用PML边界,结构如图3。
高斯型光波穿过光子晶体,在检测的一条线上被接收。位于光源正前方的接收处,坡印廷矢量与波长之间的关系如图4所示。
紧密排列的三角形晶体,与不相切的三角形晶体,在圆柱介质具有不同的折射率时,对光的透射性质不同,把图4中的带隙数值,总结为表2。
3.3. 圆柱介质构成的六角形二维光子晶体(石墨烯结构)的带隙
为了研究石墨烯结构的二维光子晶体的带隙,圆柱介质折射率分别设置为n = 1.5,1.8,2.5,介质柱半径设置为
,介质柱构成六角形(石墨烯)结构。研究两种不同的结构:介质柱相切排列,晶格常数
;介质柱不相切排列,
,整个结构的背景介质是空气,等距离排列成
方

Table 2. Transmission properties of two-dimensional triangular photonic crystals
表2. 二维三角形光子晶体的透射性质
最大带隙分别为0.07 μm和0.30 μm,已经在表中用黑体字表示。
 (1)
(1)
 (2)
(2)
Figure 3. The structure of
two-dimensional triangle photonic crystals and light source
图3.
二维三角形光子晶体的结构和光波源
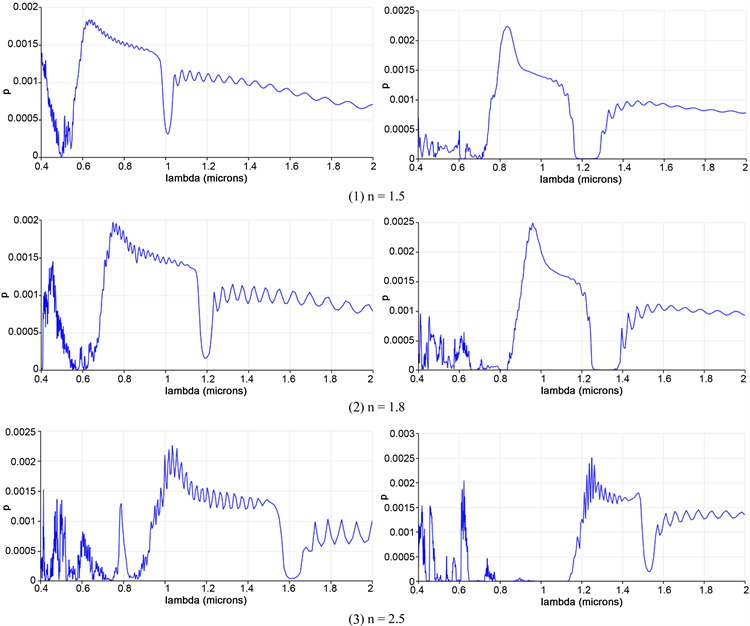
Figure 4. Transmission properties of
2-dimensional triangle photonic crystal to light waves
图4.
三角形二维光子晶体对光波的传播性质
阵,整个结构在Z方向没有长度,构成2维六角形晶体。信号源是高斯型,波长范围设置为0.4~2.0 μm,使用PML边界,结构如图5。
高斯型光波穿过光子晶体,在检测的一条线上被接收。位于光源正前方的接收处,坡印廷矢量与波长之间的关系如图6所示。
把六角形结构的二维光子晶体的对光的透射结果,总结在表3中。把最大的带隙用黑体字表示。
4. 由两种结构得到二维光子晶体的带隙叠加
在科研和工程实践中,我们往往需要宽度更大,范围更广的带隙,考虑到前面几种二维光子晶体的带隙,我们把具有比较宽大的带隙的结构进行组合,希望得到新的带隙。
4.1. 相切的正方形和不相切的正方形结构的组合
从表1数据可以看到,正方形二维结构中,相切的结构带隙最大的是n = 2.5,正方形不相切的结构,带隙最大的也是n = 2.5的结构,现在把这两种结构组合,观察组合后的光子晶体带隙(图7)。
从图8可以观察到,两种正方形结构的组合的带隙为λ = 0.5~0.53 μm,0.66~0.70 μm,0.88~0.97 μm,
 (1)
(1)
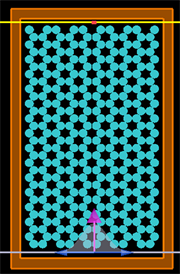 (2)
(2)
Figure 5. The structure of
two-dimensional triangle photonic crystals and light source
图5.
二维三角形光子晶体的结构和光波源
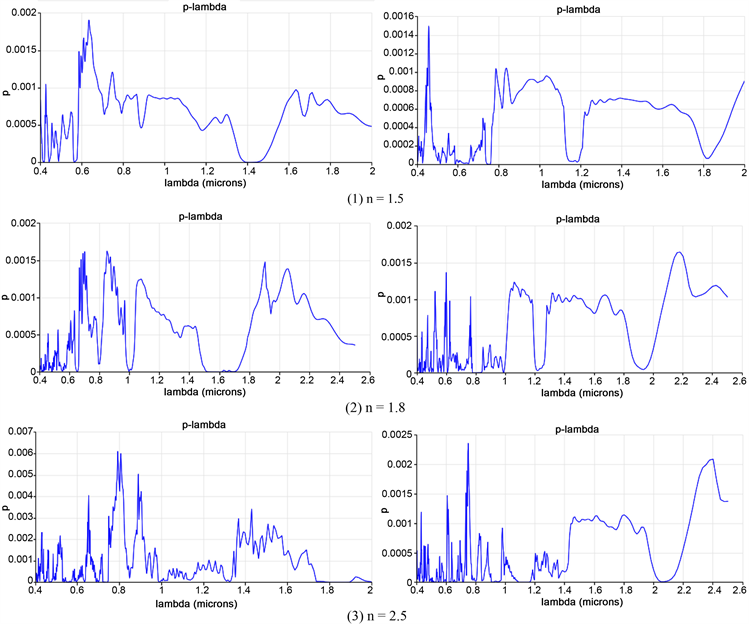
Figure 6. Transmission properties of
2-dimensional hexagonal photonic crystal to light waves
图6.
六角形二维光子晶体(石墨烯结构)对光波的传播性质

Figure 7. A combination of two square structures
图7. 两种正方形结构的组合
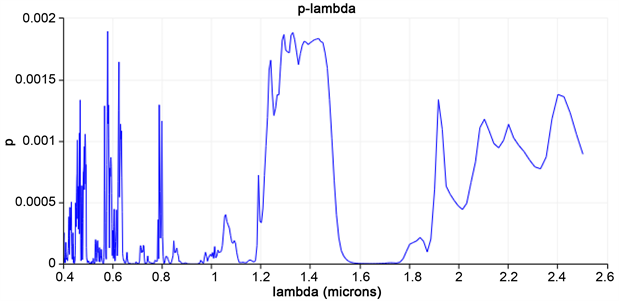
Figure 8. Transmission-wavelength relation
图8. 结构光的透射与波长关系

Table 3. Transmission properties of two-dimensional hexagonal photonic crystals (graphene structure)
表3. 二维六角形光子晶体(石墨烯结构)的透射性质
最大带隙分别为0.07 μm和0.30 μm,已经在表中用黑体字表示。
1.11~1.18 μm,1.56~1.75 μm,组合结构的带隙,再现了正方形结构的两种成份的全部的带隙。
4.2. 六角形结构和三角形结构的组合
从表2中可以看到,三角形结构中,带隙最大的是折射率n = 2.5,不相切的结构的带隙,带隙宽度
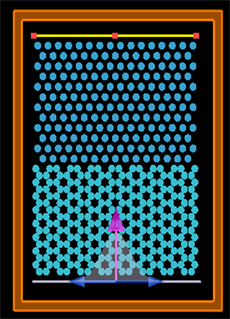
Figure 9. The combination of a triangle and a hexaganal structure
图9. 三角形和六角形结构的组合
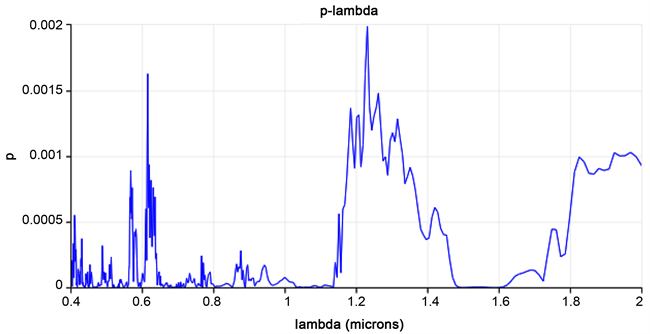
Figure 10. The band gap of a two-dimensional photonic crystal with triangular and hexagonal structures
图10. 三角形和六角形结构组合的二维光子晶体的带隙
为0.3 μm;
表3中的数据显示,六角形结构中,带隙最大的是折射率n = 1.8,相切的结构,带隙宽度为0.2 μm,但波长位置不同。现在这把两种结构组合,结构如图9。
从图10的透射图中可以看到,这种组合结构的带隙在:λ = 0.65~0.72 μm,0.80~0.85 μm,1.02~1.13 μm,1.49~1.61 μm,把组合结构的带隙和原结构的带隙相比较,三角形不相切结构的带隙完全再现,六角形相切结构的带隙λ = 1.50~1.70 μm也得到部分再现。
5. 结论
本文系统的研究了由圆柱介质构成的二维正方结构、三角形结构、六角形结构,在折射率分别为n = 1.5 (玻璃),1.8 (石墨),2.5 (石墨),圆柱之间相切和不相切的条件下的带隙,得到了完整的带隙分布;通过把两种不同的正方形结构组合后,这两种结构的带隙在组合后都得到完全的再现;三角形结构和六角形结构组合,得到组合后的带隙,三角形结构的带隙得到完全再现,六角形结构的带隙得到部分再现。六角形结构的带隙部分再现的原因,还需要进一步研究。通过分别设计两种不同带隙的材料,然后把这两种材料组合,可以得到两种材料的带隙的再现,为寻找多个宽带隙材料提供了一个新思路。
基金项目
湖北省教育科学“十二五”规划重大项目,编号2012A016。