抽水蓄能电站甩负荷过渡过程下活动导叶水力特性数值模拟研究

Numerical Simulation and Hydraulic Characteristics of Moving Guide Vane in Pumped Storage Units

摘要: 为探究抽水蓄能机组在甩负荷工况下的活动导叶水力特性，对包含全过流系统的抽蓄电站稳定发电工况及甩负荷过渡过程进行了数值模拟，并对活动导叶的水力特性进行了分析研究，获得了机组在甩负荷过程中的导叶水力矩和内流特性，发现相对于机组的稳定发电工况，导叶的水力矩在甩负荷过程中存在较大的波动，当机组转速接近飞逸转速时，水力矩出现瞬时最大值，通过对比可以发现，导叶3水力矩监测相对其它导叶最大瞬时数值较大，约为80 kN•m，其余导叶瞬时水力矩最大值均在70 kN•m左右，转轮内部的涡核旋转失速和叶片出水边出现的脱流现象是造成这种力矩波动的主要原因。

Abstract: To explore the activities of the pumped storage units in load rejection condition guide vane hy-draulic characteristics, containing the full flow system of stable power generation pump storage power station operating mode and the load rejection transient numerical simulation of the guide vane and the activities, this paper analyzes the hydraulic characteristics of the unit in the process of load rejection guide vane water moment and internal flow characteristics, finding that relative to the working condition of the stability of the power unit, the water of the guide blade moment in the larger fluctuations in load rejection process, when the unit speed is close to runaway speed and the maximum water appears instantaneous torque, can be found by comparison, and guide vane 3 water monitoring torque relative to other guide vane maximum instantaneous value is bigger. It is about 80 kN•m, and the maximum value of water moment of the other instantaneous blade is about 70 kN•m. The vortex core in the inner rotor and the out-of-water edge of the blade are the main reasons for this torque fluctuation.

1. 引言

抽水蓄能电站在电网运行中主要起调峰填谷、调频调相以及事故备用机的作用，有着较多的运行工况，这类电站为了满足电力系统动态服务的要求，往往具有一机多用、工况转换迅速、启停频繁、压力脉动剧烈的特点，由此将导致输水系统中产生复杂的水力瞬变问题。近年来利用三维CFD对水力机组过渡过程进行数值模拟的技术愈发成熟，周大庆、吴玉林等 [1] [2] [3] 采用该方法对轴流式水轮机模型飞逸过程进行研究，获得了飞逸过程中不同物理量的变化曲线，计算结果表明，所得最大飞逸转速与试验值非常接近，误差在1.5%以内，所得力矩及流量等外特性参数变化过程均符合高比转速水轮机理论特性；李金伟等 [4] [5] 利用该方法对混流式水轮机飞逸过渡过程进行了模拟，得到了水轮机达到飞逸状态时的单位流量和单位转速，并和试验结果进行了比较，结果显示两者吻合良好；张蓝国等 [6] 建立了抽水蓄能电站的三维全流道模型，并对泵工况进行了过渡过程研究，与试验数据对比表明：该方法可以准确表示电站的外特性及内流特性。上述研究表明，三维CFD技术可以有效地利用于水力机械的过渡过程研究。

本文主要利用三维CFD技术对水泵水轮机的正常发电工况和发电状态下的甩负荷工况进行数值模拟，并对两种工况下的导叶水力特性进行计算和分析，并探究导叶水力特性变化的内流机理。

2. 数值计算模型

2.1. 模型参数

选用立轴、单级、混流式水泵水轮机，转轮直径为5226.5 mm，转轮叶片数量7片；水轮机活动导叶及固定导叶个数都为20，活动导叶体高度1106 mm。水轮机工况额定水头105.8 m，额定转速为200 rpm，飞逸转速为320 rpm，额定流量为148.7 m³/s；水泵工况最大扬程130.4 m，最小扬程108.2 m，最大流量138 m³/s，最小流量为113 m³/s。

运用Proe建立机组及管路三维模型，机组全过流系统及各组成部分三维模型如图1所示。

2.2. 网格划分

为便于采用动网格方法来模拟水泵水轮机甩负荷过程中活动导叶的动态关闭过程，对活动导叶区域采用如图2中所示的混合网格进行空间离散：计算中除活动导叶区域外其余流体计算域均采用结构化网格进行空间离散。

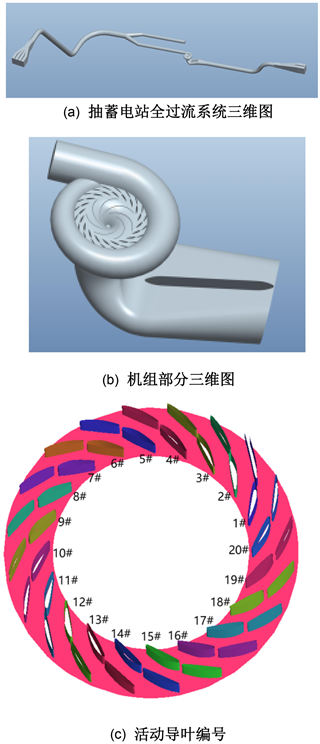
Figure 1. Three-dimensional model of full flow system and each part

图1. 机组全过流系统及各部分三维模型

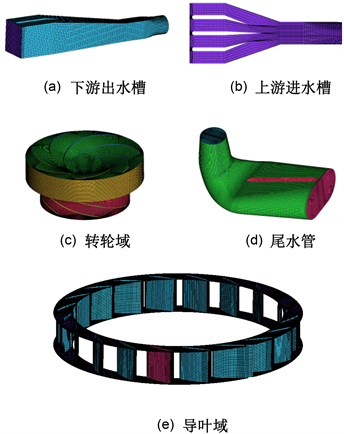
Figure 2. Grid partitioning of full flow system

图2. 全过流系统结构网格划分

3. 三维过渡过程计算方法

3.1. 控制方程与湍流模型

本文在瞬态计算中采用了SST k-ω (Shear-Stress Transport)模型。该模型是Standard k-ω是考虑剪切应力的修正模型，Standard k-ω模型基于Wilcox k-ω模型 [7] 产生，其中包括对低雷诺数效应，可压缩性和剪切流扩散的修改。Standard k-ω模型湍动能k与湍流扩散率ω的输运方程为:

$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_i}\left(\rho k{u}_i\right)=\left[{\Gamma }_k\frac{\partial k}{\partial x_j}\right]+G_k-Y_k+S_k$ (1)

$\frac{\partial }{\partial t}\left(\rho \omega \right)+\frac{\partial }{\partial x_i}\left(\rho \omega u_i\right)=\left[{\Gamma }_{\omega }\frac{\partial \omega }{\partial x_j}\right]+G_{\omega }-Y_{\omega }+S_{\omega }$ (2)

方程中，G_k是指由于速度梯度产生的湍动能。G_ω是指湍流扩散率。Y_k和Y_ω代表湍流耗散。S_k和S_ω是指用户自定义的源项。Г_k和Г_ω分别代表k和ɛ的有效扩散系数，由下式得出：

${\Gamma }_k=\mu +\frac{{\mu }_t}{{\sigma }_k}$ (3)

${\Gamma }_{\omega }=\mu +\frac{{\mu }_t}{{\sigma }_{\omega }}$ (4)

其中σ_k和σ_ω是分别为k和ɛ的湍流Prandtl数，其中湍流粘度项μ_t为：

${\mu }_t={\alpha }^{*}\frac{\rho k}{\omega }$ (5)

SST k-ω模型湍动能k与湍流扩散率ω的输运方程为：

$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_i}\left(\rho k{u}_i\right)=\left[{\Gamma }_k\frac{\partial k}{\partial x_j}\right]+G_k-Y_k+S_k$ (6)

$\frac{\partial }{\partial t}\left(\rho \omega \right)+\frac{\partial }{\partial x_i}\left(\rho \omega u_i\right)=\left[{\Gamma }_{\omega }\frac{\partial \omega }{\partial x_j}\right]+G_{\omega }-Y_{\omega }+D_{\omega }+S_{\omega }$ (7)

SST k-ω模型考虑了在湍流粘度定义中湍流剪切应力的传输。这使得SST k-ω模型比Standard k-ω模型更加精确和可靠地用于强压力梯度流、本文所选用的机组模型内部流动变化较为剧烈，故选用该模型作为湍流模型。

3.2. 离散格式与定解条件

整个模拟在FLUENT 16.0软件平台上完成，采用有限体积法离散方程组，方程组中压力项采用二阶中心差分格式，对流项、湍动能以及耗散率均采用二阶迎风格式，近壁处用壁面函数处理，应用SIMPLEC方法对流场进行联立求解。

考虑重力作用对计算的影响，考虑水体重力作用，边界条件运用用户自定义函数(UDF)将电站进出水口设置成压力沿水深的梯度变化(参考压力为标准大气压)，近壁区采用标准壁面函数。根据实际淹没深度给定上下库进出口压力，由上下游水位差压差作用带动水轮机转轮转动。引水隧洞和尾水隧洞内壁为钢筋混凝土衬砌，粗糙度设为2.5 mm，高压钢管内壁为钢衬，与蜗壳等壁面粗糙度同设为0.06 mm，转轮和导叶等过流表面粗糙度较小，设为0.0016 mm。

3.3. 数值格式与求解控制

根据转子动力学，抽水蓄能发电机组的转子角动量平衡方程为：

$M=J\frac{\text{d}\omega }{\text{d}t}$ (8)

其中，M为叶轮所受的合力矩，N∙m；J为转子的转动惯量，kg∙m²；ω为转子角速度，rad∙s⁻¹；t为时间，s。编制成FLUENT用户自定义函数(UDF)并加载到变速滑移网格的转速控制参数选项中，并在非定常流场计算的每一个时间步迭代过程中调用，从而将机组转子的转速计算与流场计算耦合到一起。

选用SST k-ω湍流模型对控制方程进行封闭，采用有限体积法离散方程组，数值计算时压力和速度的耦合使用SIMPLEC算法，进行压力修正，方程组中压力项采用二阶中心差分格式，对流项、湍动能以及耗散率均采用二阶迎风格式，近壁处用壁面函数处理，应用SIMPLEC方法对流场进行联立求解。压力项差分方式选择二阶中心差分，湍流模型使用基于剪切应力输运的两方程模型，即SST k-ω两方程模型，SST k-ω模型能能够有效地捕捉壁面附近的流动特征，能准确预测逆压梯度下的流体分离开始点和分离区大小。模型不同区域间用interface连接，用滑移网格法处理转轮旋转区域。时间步长取0.005 s，每个时间步长迭代20次。

4. 计算结果分析

4.1. 机组稳定发电运行情况下导叶水力矩特性

对机组在额定水头(最大、最小及事故水头)不同负荷(100%、75%及50%)下的性能进行了计算，由于分析得出的结论规律相似，这里主要分析最大水头，100%负荷工况下的流动特性。计算的出的导叶水力矩的值分布如下图3所示。

从图4中可以发现，导叶水力矩有周期性的规律。#2-#4为一个周期，#5-#7、#8-#9、#10-#12、#13-#15、

Figure 3. Distribution diagram of water moment value of guide vane

图3. 导叶水力矩值分布图

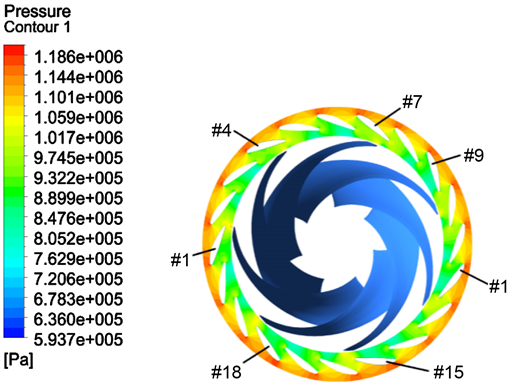
Figure 4. Pressure distribution cloud diagram of rotor and guide vane

图4. 转轮及导叶区的压力分布云图

#16-#18、#19-#1分别为一个周期。导叶水力矩的这种周期性规律与转轮叶片和导叶间的相互位置有关。为进一步说明不同导叶的水力矩差别，做出其表面压力云图进行说明。

为使导叶有关闭趋势，导叶水力矩应为正值。若导叶头部正面的压力大于背面，导叶尾部正面的压力小于背面，则有利于造成关闭趋势。从图中可以看出，水流流过导叶后，在叶片头部附近形成高压区，该高压区影响了部分导叶(图中所示)尾部附近的压力分布，使得导叶尾部附近背面压力高于正面压力，使得导叶有关闭趋势，因此这部分导叶水力矩较大。

4.2. 机组甩荷工况下的活动导叶水力矩特性

本节根据模型电站某次甩100%负荷实验相关数据选取了初始活动导叶开度Ƴ为25.5˚，试验上游水位404.7 m，下游水位290.38 m的工况进行数值模拟。模拟过程中，0 s时刻机组进行甩负荷开始，活动导叶开始关闭，导叶关闭规律如表1所示。

4.2.1. 甩负荷活动导叶水力矩计算

计算过程每个时间步长监测一次各个导叶所受的合水力矩数值(200 Hz)，通过数值计算监测得到甩负荷过程20个活动导叶所受水力矩变化，由于甩负荷过程各导叶关闭所受水力矩变化规律相似，限于篇幅，选取部分导叶水力矩计算结果进行出图分析，如图5所示，可以看到整个甩负荷过程中导叶水力矩方向基本都与导叶关闭转向相反，变化规律基本一致，但都存在数值大幅度剧烈震荡变化现象，这是由于机组甩负荷过程中活动导叶关闭，导叶区域瞬态内流特性复杂不稳定，翼型两侧流动压差变化剧烈引起导叶合力矩大小方向以及作用点的瞬时变化。甩负荷发生时，水力矩变化增加，当机组转速接近飞逸转速时，水力矩出现瞬时最大值，通过对比可以发现，导叶3水力矩监测相对其他导叶最大瞬时数值较大，约为80 kN∙m，其余导瞬时叶水力矩最大值均在70 kN∙m左右，活动导叶相对于蜗壳的位置以及水流流

Table 1. Closing rule of movable guide vane

表1. 活动导叶关闭规律

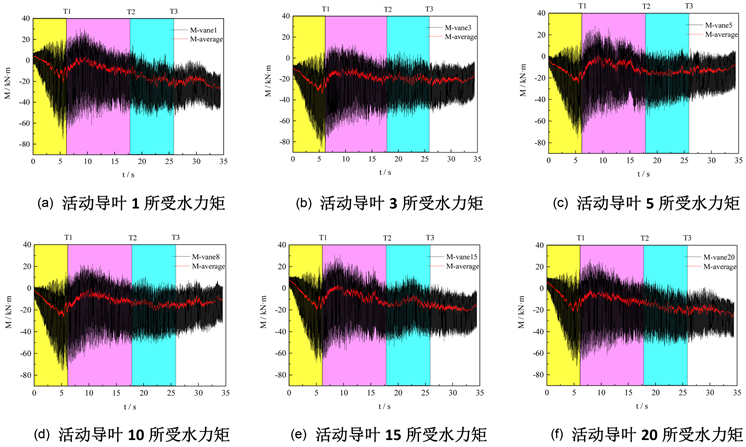
Figure 5. Hydraulic moment of moving guide vane

图5. 活动导叶水力矩

态受蜗壳形状变化是造成各个导叶水力矩数值变化大小不完全一致的主要因素；进入制动过程后，水力矩震荡减小，伴随机组转速降低流量减小，各导叶水力矩基本维持相对稳定变化，幅值呈现减小趋势。为明确甩负荷过程中活动导叶水力矩数值变化趋势，将所监测到水力矩进行时均化处理，每隔20个步长数值进行时均化，所得到的水力矩时均变化曲线如图5所示，可以看到时均处理后的各导叶水力矩随时间变化规律较为明显并且平均值远小于瞬时最大值。

4.2.2. 机组甩负荷动态内流特性

1) 活动导叶区压力及流速变化

导叶在关闭过程中，随着机组转速与流量的变化导致导叶内外侧压力发生相应改变，通过图6可以看出甩负荷发生后，因导叶关闭过程中转动位置发生改变，导叶受水压力作用位置发生变化，伴随水流流速降低，水体的动能转化为压力能作用在导叶外侧区域，致使导叶外侧压力明显升高；流量转速以及导叶相对位置的瞬时变化导致活动导叶冲角增加，导致水流直接撞击翼型外侧，使得导叶外缘靠近进水边出压力增大。甩负荷进入制动区后，导叶受压升高，水力矩波动增加；至25 s后则因转速流量的降低，

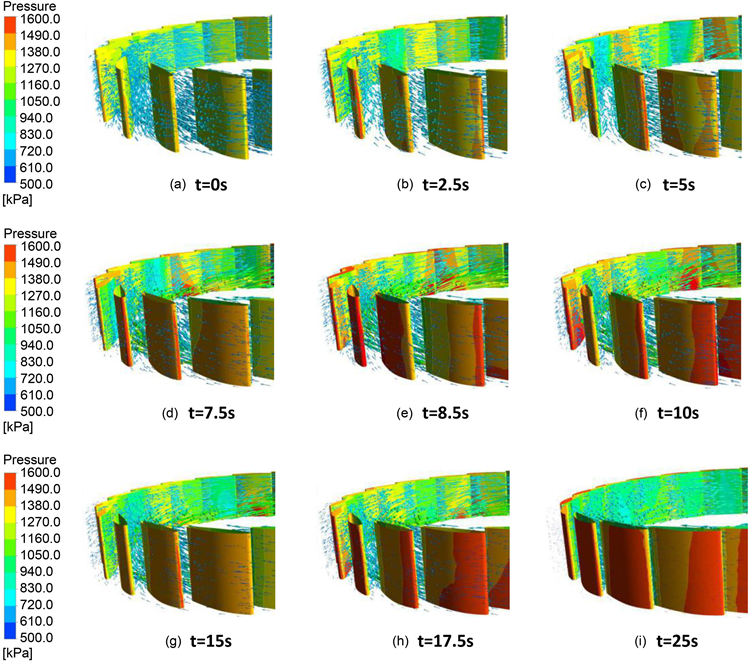
Figure 6. Pressure cloud map of moving guide vane region

图6. 活动导叶区压力云图

动能减小，导叶内侧区域压力相对增加，导致水力矩数值变化相对稳定，可以看到进入制动区后活动导叶压力呈现较大周期的波动变化。

2) 中心截面内流变化

通过观察甩负荷过程湍动能变化图7可以看出，甩负荷发生后，伴随转速升高，流态变化，湍流强度由叶片压力面中心流域处逐渐增大。而当机组达到飞逸转速时(6.51 s)，湍流强度并非到达极值，而是存在于进入反水轮机工况1 s左右时；可以看到叶片进水边处湍流强度相对较大，这是因为机组转速流量的降低以及活动导叶关闭过程中出水角的改变影响到转轮入流角的变化，形成脱流，并且转轮外援侧周向流速较大，导致叶片靠近进水区域流道湍动能较大，但随后伴随转速流量的持续下降，湍流强度逐渐降低。

由图8可见，甩负荷发生后，无叶区附近涡核分布略有减小；而通过涡核变化趋势可以看出，涡核发生于叶片吸力面靠近出水边一侧，因水泵水轮机转轮尺寸较大，叶片子流道相比于常规水轮机转轮较为狭长，因此伴随转速升高，即使处于水轮机工况，但依旧存在显著的水泵离心作用，涡核受离心作用影响逐渐向转轮进口扩散，但因流量转速的瞬时变化，水流流向抑制涡核向无叶区扩散，在转轮力矩趋于0的时刻(t = 6.51 s)，涡核在子流道内出现破碎，逐渐向叶片进口处发展分布，逐渐堵塞流道且现象随时间变化愈加明显，而涡核破碎过程伴随的能量变化这刚好与前面的转轮水力矩高强度区域(图5)相对应，由此可以断定甩负荷过程中转轮和活动导叶水力矩的不稳定特性是由转轮域至无叶区的大量涡核发展分布对应的特殊流动导致的；而旋涡伴随转轮也以一定得角速度转动，形成旋转失速现象，引发转轮内部

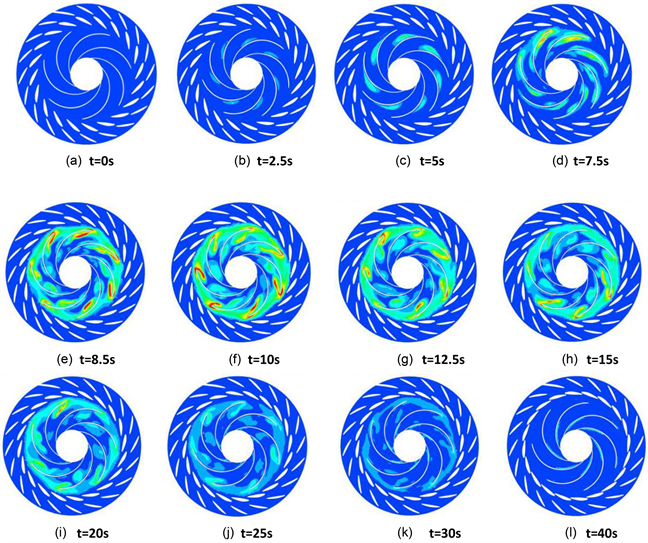
Figure 7. Central section turbulent kinetic energy transformation diagram

图7. 中心截面湍动能变化图

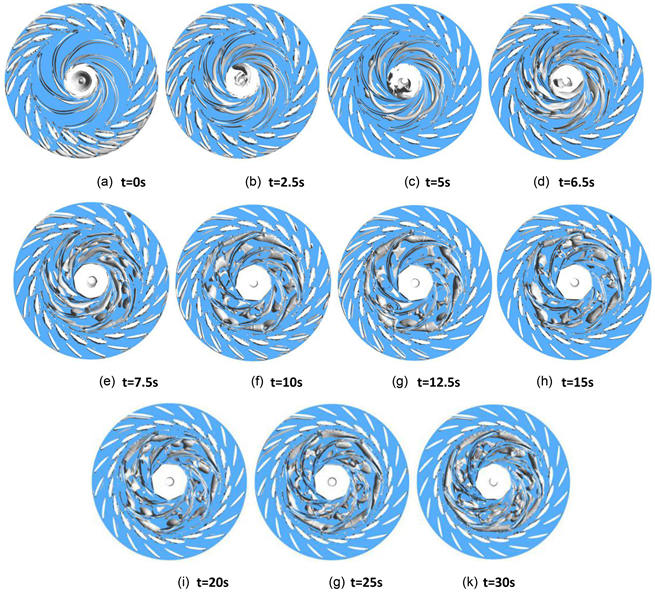
Figure 8. Distribution diagram of core vortex at center section

图8. 中心截面涡核分布图

流量分布极为不均匀，造成流道阻塞流量减小，转轮受力呈现非对称性，诱发转轮乃至整个机组水力激振，引发叶片及相关部件疲劳断裂情况发生，失速涡中心产生的低压区造成转轮出口的周期性横流流动对主轴也有一定冲击；且伴随涡核破灭耗散，对导叶内侧压力变化产生较大影响，可以看到图6导叶内侧压力梯度变化较大，致使导叶水力矩变化波动幅值较大。

3) 叶轮内流变化

通过转轮纵截面流线变化图9可以看出，甩负荷发生后，转轮出水边脱流现象明显，率先诱发涡旋流动，随后伴随转轮高速转动下的水泵效应漩涡逐渐向转轮子流道区域扩展耗散直至无叶区，漩涡的发展演变伴随着大量的能量转换，转轮叶片受力稳定性差，引发水力激振，这也是引起转轮以及导叶水力矩波动变化的原因之一。对于叶片，旋转失速出现后，流动在叶片背面存在分离，叶片正面受到水流的冲击，旋涡初生于叶片背面。于是在制动工况下，叶片将承受较大的交变应力，这对叶片强度及表面材料都提出了更高的要求。

通过对比图8可以看出，从转轮流道流线分布可以看出约从t = 10 s时刻开始叶片子流道涡核发展破碎延伸到转轮出口，造成活动导叶出口形成涡核占据无叶区，这种涡旋会压缩过流区间，使得水流从被迫从导叶出水侧以极高的流速冲击到叶片的压力面，这也是叶片压力面以及活动导叶内侧面区域形成局部高压的原因。随着时间演进，转轮叶片内的流线愈发紊乱，叶片背水面进口形成回流涡结构越来越大，

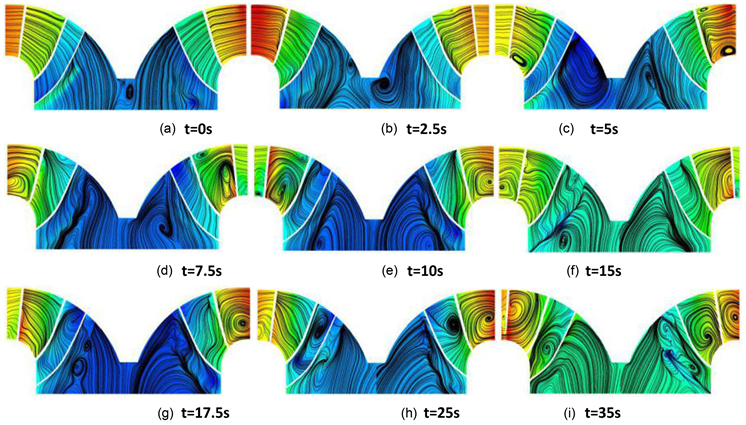
Figure 9. Flow line variation diagram of the runner section

图9. 转轮截面流线变化图

整个涡的纵向尺寸占据了流道的1/2至2/3，使得主流被更多的挤向转轮上冠下环区域，导致转轮轴向力剧烈变化发生引发机组振动，而这些涡旋的阻塞流动是造成水泵水轮机反“S”区特性的一个重要原因。

而机组进入飞逸转速代表着甩负荷进入反“S”区，此时导叶相对开度较大，水流与转轮叶片进口间的较大冲角，而狭长的转轮叶片产生的较大离心力，使得在活动导叶和转轮进口的无叶片区域形成的旋水环，大大阻碍了进入转轮的流量；同时，导叶低压面少量涡形成的脱流，转轮叶片低压面并延伸到相邻叶片高压面的较大附着的涡，以及在叶片尾部脱流产生的二次涡，都使得流量减小。

受水流冲击作用，转轮叶片压力大小沿径向向内侧呈逐渐递减变化，伴随甩负荷开始，转轮叶片压力面变化集中在上冠叶片出水边处，如图10所示。这是由于出叶片水边脱流诱发漩涡产生集中在转轮出水侧区域导致涡旋分布影响叶片压力变化；而甩负荷过程冲角的改变导致叶片进水侧出现局部低压区，引发进水流道涡旋流的产生。

而甩负荷发生后，由于漩涡的产生发展产生流场的压力变化直接作用于叶片吸力面侧，导致叶片吸力面一侧压力变化较为显著。伴随涡旋的扩展，无叶区及导叶内部出现涡阻滞流动，局部高压向叶片内部发展范围扩大，这种叶片进口高压区会逐渐在所有叶片上出现，且逐渐向转轮内部延伸，使得转轮内部出现了明显的高压区与低压区分界。

通过图11可以看到，甩负荷发生后，低压区明显增多，且呈现周向不均匀分布，集中分布在靠近叶片出水侧；并且25 s前后出现压力分布整体骤降现象，这可能是因为甩负荷过程中机组转速流量的变化引起流场复杂变化导致水击现象的产生，由此产生了大幅度的压力变化导致整个机组流域压力骤降。

机组达到飞逸转速后进入制动区，此时活动导叶开度依旧较大，由于转速和流量的减少使得机组转轮进口冲角瞬时增大率大于活动导叶出水角的降低率，水流在叶片吸力面进水侧靠近叶缘处发生撞击形成高压，在叶片压力面进水侧叶缘处出现脱流产生负压，转轮叶片受力变得极为不均匀容易引起疲劳破坏，但伴随转速流量的降低以及活动导叶出水角的改变，高压区逐渐减小。

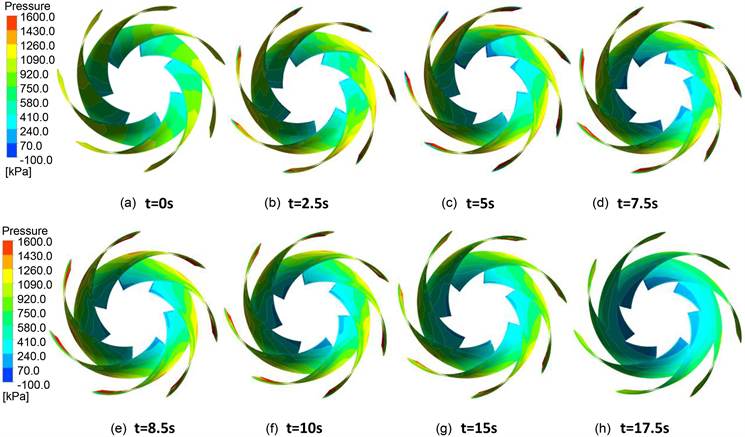
Figure 10. Pressure variation diagram of blade pressure surface

图10. 叶片压力面压力变化图

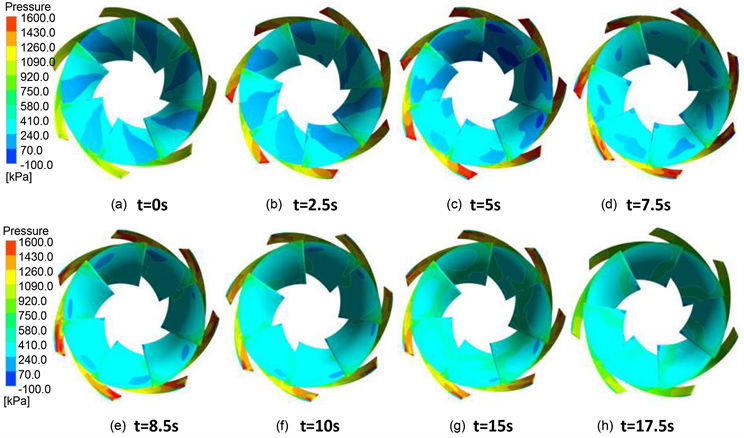
Figure 11. Pressure variation diagram of blade suction surface

图11. 叶片吸力面压力变化图

而转轮进出口存在这些脱流在部分流动内逐步发展成面积较大的环流，造成流道拥塞。水流被迫流向其他流道，引起流量的重新分配，进而导致转轮的转动矩、转速的波动以及运行的不稳定。这点可以根据活动导叶流道内的流态变化得到进一步的解释，当活动导叶部分流道内出现涡流时，流道间的流量同样会重新分配，由此初步判断将导致活动导叶所受水力矩产生波动，进而引起导叶开度出现波动加剧转速的波动。

5. 结论

本文主要建立抽水蓄能电站的三维全流道模型，利用三维湍流计算方法对模型进行稳定发电运行、发电机工况甩负荷飞逸过渡过程两种工况进行了数值模拟，并对活动导叶的水力特性进行了计算和分析，主要结论如下。

1) 机组稳定发电情况下，机组各导叶所受水力矩各不相同，呈现一种周期性分布的规律。且导叶开度变化会导致水力矩的变化。导叶水力矩的这种周期性规律与转轮叶片和导叶间的相互位置有关。

2) 机组在甩负荷过程中导叶水力矩方向基本都与导叶关闭转向相反，变化规律相同。机组在甩负荷过程中，导叶的水力矩数值存在较大范围的波动，主要原因是活动导叶在关闭过程中导叶区域的流动较为复杂且不稳定。

3) 通过分析转轮内部的涡核分布情况，分析得出甩负荷过程中转轮和活动导叶水力矩的不稳定特性是由转轮域至无叶区的大量涡核发展分布对应的特殊流动导致的；而旋涡伴随转轮也以一定的角速度转动，形成旋转失速现象，引发转轮内部流量分布极为不均匀，造成流道阻塞流量减小，转轮受力呈现非对称性，容易诱发转轮乃至整个机组水力激振。

4) 通过观察叶轮内部流动分布，可以看出在甩负荷发生后转轮出水边脱流现象明显，率先诱发涡旋流动，旋涡的发展伴随着能量的变化，这也是引起转轮以及导叶水力矩波动变化的原因之一。

基金项目

国家电网公司科技项目资助(合同号：SGBXSJJS1700007)。

NOTES

^*通讯作者。