基于全站仪坐标测量的立式储罐变形检验方法研究

Research on Deformation Detection Method of Vertical Storage Tank Based on Total Station Coordinate Measurement

摘要: 通过总结全站仪坐标测量原理及误差分析，提出将其用于大型立式储油罐体变形检验的一种检测方法，总结了常见罐体圆度、垂直度、凹凸变形等尺寸误差检验的工作流程和数据分析方法，同时还讨论了浮顶变形相关的检测方法，并通过实际工程中的实例罐体检验验证，证实了全站仪坐标测量方法用于立式储罐变形检验的适用性和有效性，为今后圆筒状立式储油罐体的变形检验工作提供了一种便捷有效的检验方法。

Abstract: By summarizing the principle of total station coordinate measurement and error analysis, a method of measuring deformation of large vertical oil storage tank is put forward. The workflow and data analysis methods of measuring dimensional errors, such as roundness, verticality, concave-convex deformation of tank, are summarized. Meanwhile, the detection methods related to floating roof deformation are also discussed. The applicability and validity of the total station coordinate measuring method for deformation inspection of vertical storage tanks are verified by a practical engineering example. It provides a convenient and effective method for deformation inspection of cylindrical vertical storage tanks in the future.

1. 引言

钢制立式储油罐体作为原油储备运输的重要设备，其具有省材料、占地少、投资省、储量大、易操作等优点，也是大多数国家广为采用的石油储存设备之一 [1] 。随着近20年来我国经济发展和使用需求的快速增长，石油储量越来越多，储罐规模逐步向大型、超大型方向发展，目前应用最为广泛的为立式圆筒状钢制浮顶储罐，容积一般以5万立方和10万立方居多。储罐规模的大型化和结构复杂完善化发展，给我国石油石化行业的原油存储、转运、输送带来极大便利的同时，也造成影响其安全稳定的因素更为复杂多样。尤其当储罐在运营使用过久或受到其它因素影响导致发生倾斜变形、浮盘沉盘，甚至沉顶、翻顶等问题后，其罐体的圆度、局部凹凸变形、垂直度等均会发生较大变化，对储罐安全和基地生产带来严重隐患，甚至发生重大安全事故 [2] [3] 。因此，针对储油罐体在运营服役一定时期后，对其结构变形情况和安全状态进行准确有效检验就尤为重要。

现有的储罐变形检测主要针对外观质量检测，对其完整的变形情况往往无法进行准确、有效、经济高效的获取，又或需采用三维激光扫描等复杂技术才能得以实现，但设备成本过高、后期数据处理过于复杂，导致针对罐体的各项变形检验尚无快捷有效的方法 [4] [5] [6] [7] 。全站仪坐标测量为现下工程领域发展较快、技术成熟、结果可靠的测量方法之一，本文结合全站仪坐标测量原理及技术，详细总结了其用于储罐各项变形检验项目的工作流程及计算过程，并运用至实际的储罐变形检测项目进行验证，实践表明该方法对储罐变形检验有效且较为准确，为储罐的安全运营和变形修复提供了可靠依据。

2. 全站仪坐标测量及误差分析

全站仪为当前工程测量所应用的主要设备之一，其在土木、交通、矿山、水利、能源等各个领域均应用广泛。其空间点位坐标测量原理为空间球坐标测量的原理，即已知一现有点坐标，假设全站仪对目标待测点的水平角、垂直角(天顶距)、斜距分别为(α, β, D)，根据右手坐标系可得出待测点P的空间三维坐标为：

$\{\begin{array}{l}x=D\sin \beta \cos \alpha \\ y=D\sin \beta \sin \alpha \\ z=D\cos \beta \end{array}$ (1)

测量示意图如图1所示。此外，根据范百兴等 [8] [9] [10] 研究成果，可计算不同型号全站仪测量时测量点坐标的中误差值。以TS30全站仪为例，其测角误差为0.5''，测距误差为0.6 + 1 ppm，计算得出其坐标点位测量误差估算值如表1示。从表可见，TS30全站以用于坐标测量的点位误差坐标基本都在2 mm以下，足以满足绝大多数结构物体的变形测量应用。

Table 1. Estimation error of coordinate point position measurement for TS30 total station

表1. TS30全站仪坐标点位测量误差估算值表

注：其中m_pc为平面坐标误差；m_p为空间坐标误差；m_z为Z方向垂直坐标误差。

3. 基于坐标测量的罐体变形检验方法

3.1. 测量方式和工作流程

大型储油罐体外观变形检验主要包括罐体几何圆度、罐壁垂直度、罐壁凹凸度、导向油管垂直度、以及浮顶相关的变形检测等内容。主要工作方式为根据全站仪坐标测量原理，对罐体各部分组件设立若干测点，并进行平面坐标测量和三角高程测量，再根据测点坐标，建立局部坐标系，并采用平差法进行坐标计算并绘图，以最终确定罐体各部分的几何变形情况。

测量工作可根据《立式圆筒形钢制焊接储罐施工规范》(GB50128-2014)的有关要求 [11] ，结合待测罐体的实际情况，将立式圆柱形罐体分为6~9个观测截面，每个观测截面在东、南、西、北及各45˚夹角方位上布设24~36个测点。测量检验前，先在罐体内部中心位置处安置全站仪，并预设该点为(0, 0, 0)或其他坐标均可，照准北方或可瞄准一固定参照物为北向进行后视定向，设置测量参数，再根据测量需要选择棱镜或免棱镜测量，逐个测量各个测点坐标。观测示意图如图1所示，采用假定坐标系设置测站坐标及后视定向，仪器所在位置坐标设为(0, 0) (仪器位置不在罐中心)，X轴指向北方向，Y轴指向东方向。

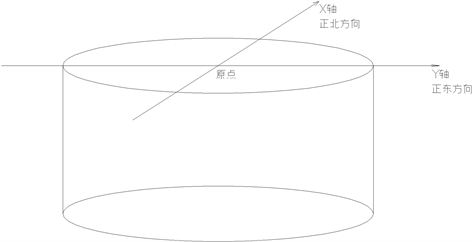
Figure 1. Schematic diagram of observation coordinates

图1. 观测坐标示意图

3.2. 数据处理方法

测量数据采用平差法进行计算，平差法为测量数据处理中最常采用的方法之一，包括条件平差、间接平差等，所有经典的平差计算均是基于最小二乘法原则对测量数据误差进行调整计算 [12] [13] [14] 。本文的平差计算主要采用计算机条件法进行严密平差，各期平差计算采用统一的起算数据进行。此外，观测成果计算和分析中的数值取位符合需精确到0.01 mm。

如已知点坐标为： $A\left(X_A,Y_A\right)$ ， $B\left(X_B,Y_B\right)$ ，待定点：P (需计算其坐标)，观测数据：a, b (g = 180 − a − b)，计算各边方位角：

$\begin{array}{l}{\alpha }_{AB}={\tan }^{-1}\frac{y_B-y_A}{x_B-x_A}\\ {\alpha }_{AP}={\alpha }_{AB}-\alpha \\ {\alpha }_{BP}={\alpha }_{BA}+\beta \end{array}$ (2)

其各边长度得：

$\begin{array}{l}c=\sqrt{{\left(x_B-x_A\right)}^2+{\left(y_B-y_A\right)}^2}\\ a=c\cdot \frac{\sin \alpha }{\sin \gamma },b=c\cdot \frac{\sin \beta }{\sin \gamma }\end{array}$ (3)

则待测点P的坐标如下：

$\begin{array}{l}{x}_P=x_A+b\cdot \cos {\alpha }_{AP}\\ y_P=y_A+b\cdot \sin {\alpha }_{AP}\\ x_P=x_B+a\cdot \cos {\alpha }_{BP}\\ y_P=y_B+a\cdot \sin {\alpha }_{BP}\end{array}$ (4)

1) 圆心点坐标计算

根据圆的一般公式： $x^2+y^2+Dx+Ey+F=0$ ，为达到测量数据与拟合函数之间误差的平方和为最小，可将其改写为：

$M={\displaystyle {\sum }_{i=1}^n{\left(x_i^2+y_i^2+D{x}_i+E{y}_i+F\right)}^2}$ (5)

令：

$\frac{\partial M}{\partial D}=\frac{\partial M}{\partial E}=\frac{\partial M}{\partial F}=0$

则可将式(5)转换为线性方程组，整理合并为：

$\{\begin{array}{l}D{\displaystyle {\sum }_{i=1}^n{x}_i^2}+E{\displaystyle {\sum }_{i=1}^n{x}_i{y}_i}+F{\displaystyle {\sum }_{i=1}^n{x}_i}=-{\displaystyle {\sum }_{i=1}^n{x}_i^3-{\displaystyle {\sum }_{i=1}^n{x}_i{y}_i^2}}\\ D{\displaystyle {\sum }_{i=1}^n{x}_i}{y}_i+E{\displaystyle {\sum }_{i=1}^n{y}_i^2}+F{\displaystyle {\sum }_{i=1}^n{y}_i}=-{\displaystyle {\sum }_{i=1}^n{x}_i^2{y}_i-{\displaystyle {\sum }_{i=1}^n{y}_i^3}}\\ D{\displaystyle {\sum }_{i=1}^n{x}_i}+E{\displaystyle {\sum }_{i=1}^n{y}_i}+nF=-{\displaystyle {\sum }_{i=1}^n{x}_i^2-{\displaystyle {\sum }_{i=1}^n{y}_i^2}}\end{array}$ (6)

求解方程组(6)可获得D、E、F的相应数值，并由此可以得出圆心坐标为 $\left(-\frac{D}{2},-\frac{E}{2}\right)$ 。

2) 圆度误差计算

根据前述圆心坐标计算中求解计算得出的圆心坐标为 $\left(-\frac{D}{2},-\frac{E}{2}\right)$ ，圆半径为 $\sqrt{\frac{D^2+E^2-4F}{4}}$ ，并根

据拟合圆心和半径计算出圆心坐标至各测点的实测半径值，据此计算储油罐体测量断面各测点的半径偏差以及圆度误差，圆度误差计算方法为最大半径与最小半径之差和拟合半径的比值，以百分比表示，计算示意图如图2。

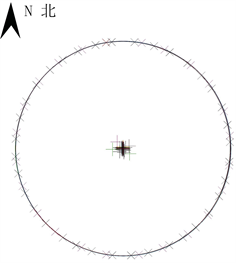
Figure 2. Schematic diagram of roundness error calculation

图2. 圆度误差计算示意图

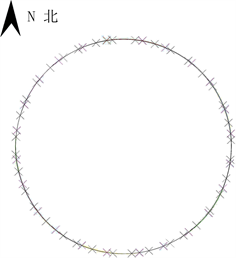
Figure 3. Schematic diagram of measurement and calculation of local concave and convex deformation

图3. 局部凹凸变形测量及计算示意图

3) 罐壁局部凹凸变形计算

通过现场测量点进行拟合得出圆心坐标与半径后，计算罐壁各点对应半径，即可得出罐壁各点位置的局部凹凸变形值，计算示意图如图3所示。但是，由于罐壁现场测量点有限，现有的检测方法仅根据所测测点值给出有限点的变形情况，但是无法准确体现罐壁圆弧表面的全面变形情况，故可采用三次样条函数插值计算方法进行拟合计算圆弧表面的变形，计算可采用MATLAB编程进行，据此可得出整个罐壁圆弧表面的局部凹凸变形情况。

4) 导向油管和罐壁垂直度计算

导向油管和罐壁垂直度计算方法均利用投影在同一点上的罐顶观测点和罐底观测点坐标进行计算 [15] ，罐体整体垂直度是通过罐顶圆心与罐底圆心坐标的投影偏差进行计算。其计算公式如式(7)所示，计算示意图如图4所示。

$\Delta =\frac{\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2}}{H}\times 100\%$ (7)

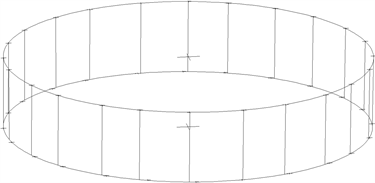
Figure 4. Schematic diagram of measurement and calculation of verticality of tank wall

图4. 罐壁垂直度测量及计算示意图

5) 扶梯中心线与导轨中心线偏差计算

储油罐体内部设有通行扶梯，扶梯下方与位于浮顶上方的导轨相接，以供人员检修等使用，由于罐体体积大、高度深，扶梯在使用过程中会出现晃动、偏移等，导致其与下部导轨会出现偏差甚至脱离，故在进行变形检验时也需对其中心偏差进行检测校对。扶梯中心线与导轨中心偏差检验可采用多点测量的方式，即测量各点的坐标，再进行平面投影，以做图形比对，进而从成果图上量测其偏差值，如图5所示。

Figure 5. Schematic diagram of deviation between escalator and guide rail center

图5. 扶梯与导轨中心偏差测量示意图

6) 浮顶部分变形检验计算

立式储油罐体内设钢制浮顶，其结构分上下两层，中部设有浮舱，浮顶下盘设有钢制立柱，以便原油排空后浮顶下落支撑至罐底；浮顶上盘上部设有排水孔及浮舱人孔人若干。油罐在使用过程中往往因为各种因素会导致浮顶出现不同程度的变形，因此也需进行检验计算，现有的凹凸变形检测方法主要采用1 m长直式样板进行间歇测量，所测结果仅为相对变形值，对某一区域整体大面积变形或浮盘各区域准确变形值尚无法得出，本文提出的主要采用方法为下盘凹凸变形利用立柱支撑点坐标实测与设计值对比，上盘采用直接测量的方式进行计算分析，可得出浮盘整体的凹凸变形情况。

4. 实测工程案例分析

4.1. 工程概况

某储油基地43号成品油储罐为立式双盘内浮顶钢制圆柱形储罐，公称容积100,000 m³，直径为80 m，罐壁高度为21.8 m，由9层不同厚度钢板焊接而成，壁板公称厚度从下至上分别为：6~9#层12 mm、5#层15 mm、4#层18.5 mm、3#层21.5 mm、2#层27 mm和1#层32 mm，单层高度2.44 m (1#层除外)。内浮顶为上下两层双盘式结构，上浮盘中心与边缘高，中间圈层底，设计坡度1.5%；下浮盘为同一设计高度，浮盘与罐底设有8层支柱支撑，罐底中心高，外侧低，坡度为0.8%，其中下浮盘边缘距罐底上表面原设计高度1.8 m，如图6所示。自2009年开始使用起，经过8年多使用，期间未对其进行过任何变形及质量检测，2017年中由于罐内积水过多且浮盘排水孔堵塞导致浮盘发生整体倾覆，肉眼可见罐壁内侧有大量擦痕，且下浮盘有明显凹凸变形，如图7所示。故此，罐体各部件变形及是否会影响安全生产情况未知，需对该储罐进行全面变形检测，以掌握其整体变形情况，为储罐修复和安全生产提供技术支持和参考。拟对其进行检测的主要内容包括：1) 储罐不同壁厚处罐壁的几何圆度；2) 储罐罐壁及整体垂直度；3) 储罐罐壁局部凹凸变形；4) 导向油管的垂直度；5) 扶梯中心线与导轨中心线偏差；6) 浮顶下浮盘凹凸变形；7) 浮顶上部排水孔与倾斜变形部分浮舱人孔高差。

测量选用徕卡TS30全站仪，采用相对坐标系，原点设在罐底中心，以扶梯中心为北向。针对罐壁从底至顶布设了6个断面，每层24个测量点；扶梯从下往上，布设测点5个，导轨从扶梯连接处往罐内，布设测点3个；浮顶下盘凹凸变形测量采用沿支撑立柱布设测点的方式，共布置8圈188个测点，各圈测点起点均以导向油管及扶梯下方的出入口为起点(测量北向)，同时针对南侧变形较大区域进行了加密测量，共布设加密点20个。根据设计原图，浮顶下盘原设计标高均为同一个标高水平，为一水平圆盘，故在对其凹凸变形检测时以中心高程为基准水平，进行比对计算；上浮盘检测排水孔2个，紧急排水孔4个以及浮舱人孔23个，主要针对浮顶倾斜变形区域进行检测。

Figure 6. Appearance of 100000 m³ storage tank

图6. 10万立方储罐外观图片

Figure 7. Internal state of storage tank

图7. 储罐内部状态照片

4.2. 数据处理及结果

根据前述检测和计算方法，获得了该立式储油罐体的各项变形情况，具体结果见表2、表3所示，其浮顶下盘凹凸变形检验结果及示意见图8。

Table 2. Detection results of appearance and deformation of No. 43 vertical storage tank

表2. 43号立式储罐外观变形检测结果

Table 3. Detection results of floating roof deformation of No. 43 vertical storage tank

表3. 43号立式储罐浮顶变形检测结果

从表2、表3以及图8可以看出，储罐罐壁最大凹凸变形值分别为12.298 mm和−17.449 mm，罐体圆度误差最大为0.297%，罐体圆心垂直度为0.112%，导向油管垂直度分别为0.174%和0.075%，浮顶下盘倾斜变形区最大凹凸变形为41 mm和−155 mm，排水孔与人舱浮孔最小高差为245 mm。参考《立式圆筒形钢制焊接储罐施工规范》(GB50128-2014)的相关规定 [11] ，可得出该储油罐体变形检验的主要结果如下：

1) 各层罐壁圆度误差均超出施工验收规范要求。

2) 储罐壁板局部凹凸偏差中，第一层(壁厚32 mm)、第二层(壁厚27 mm)及第四层(壁厚18.5 mm)超出验收规范要求，其余各层符合要求。

3) 罐壁垂直度在北、西方向略超出验收规范要求，储罐整体垂直度符合规范要求，偏移方向为北侧(即扶梯侧方向)。

4) 对比原设计资料，浮顶下盘整体下沉，且下沉量从内往外逐步增大；各测点高差负值表明浮盘相对原标准高度有下沉或凸出鼓起，高差为正值表明浮盘相对原高度上隆或向上凹陷隆起。其中A/B/C/D三层变形上凹变形量有超过原设计高度，整体各层最大凹凸变形差值约60 mm，大致圈定三个凹凸变形较大区域位置如图8示。

5) 各浮舱人孔与北侧(扶梯侧)排水孔的高差最小为0.245 m，最大为0.302 m；与南侧排水孔的高差最小为0.476 m，最大为0.493 m。各人孔与北侧和南侧排水孔的高差明显不一致，北侧低于南侧，说明此区域浮盘较南侧有明显变形，与浮顶下盘凹凸变形测量结果基本一致。

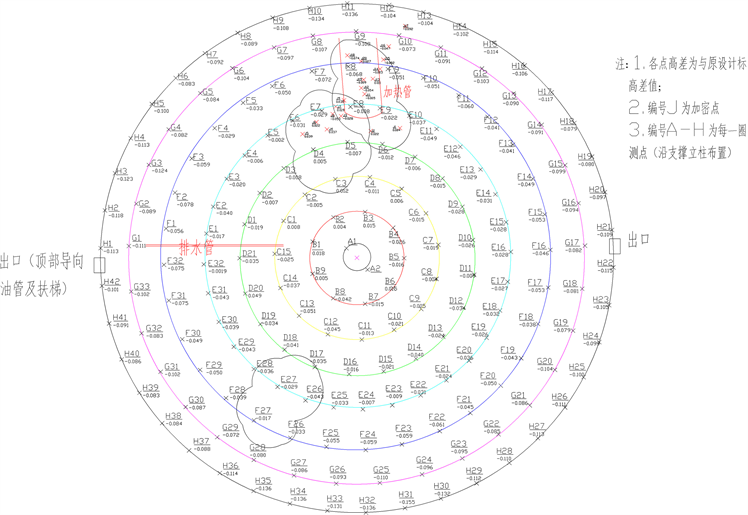
Figure 8. Sketch map of concave and convex deformation detection for floating roof footwall

图8. 浮顶下盘凹凸变形检测示意图

5. 结论

本文通过分析全站仪坐标测量的原理及误差估算，提出基于坐标测量的储油罐体变形检验方法，总结出罐体圆度、垂直度、凹凸变形、浮顶变形等检测内容的工作流程和数据分析处理方法，并通过某一实际工程案例的立式储罐变形检验验证，获得了较为准确有效的储罐变形数据，并为其使用修复和安全生产提供了数据参考，同时证实了全站仪坐标测量方法用于立式储罐变形检验工作的适用性和有效性，也为今后类似各型储油罐体的变形检验工作提供了一种经济、便捷、有效的检验方法。

基金项目

中央高校基本科研业务费(FRF-BD-17-006A)；国家重点研发计划项目资助(2016YFC0600703)。