基于静载试验的既有桥梁健康状况评估

Assessment of Existing Bridge Health Status Based on the Static Load Test

摘要: 本文结合某既有桥梁，建立桥梁结构有限元模型，模拟计算不同工况下桥梁受力与变形情况，确定桥梁静载试验的监控截面及监控点，通过不同的加载方案，得到了桥梁在不同受力状态下关键部位的变形及受力数据，对比实际监测与理论计算值，对桥梁整体健康安全状况进行评价，为以后桥梁检测中的静载试验及健康状况评价提供一些参考。

Abstract: The force and deformation of bridge under different working conditions are calculated through the finite element model of an existing bridge structure. The monitoring section and monitoring point of the static load test are determined based on the calculation results. The deformation and stress of key parts of the bridge under different stress states are monitored under different working conditions. The health case of the bridge is evaluated by means of comparing actual monitoring data with theoretical calculation data. It provides some references for the static load test and health evaluation of bridge detection in the future.

1. 引言

随着基础设施建设项目中桥梁的大量使用，既有桥梁随着使用时间的增加，桥体会逐渐出现损伤、老化等现象，桥梁梁体表面会出现渗漏水、细小裂缝、支座变形等现象，当以上表观现象累积到一定程度就会对桥梁整体结构安全带来影响，定期或不定期对桥梁健康安全状态进行监测评价是确保桥梁正常使用的前提和关键因素。目前对桥梁健康状况评价大多是通过桥梁在不同使用状态下的各项指标的监测和测试实现的，如英国工程师在Foyle连续钢箱梁上布置传感器，收集桥梁在车辆运行及风荷载作用下主梁的振动、挠度和应变情况，以此分析、判断桥梁的健康状况 [1] [2] [3] 。而目前国内对大型桥梁的监测、评估均有较多的实际案例，如武汉的跨长江的白沙洲大桥、江苏的江阴长江大桥等均安装了健康监测用的传感设备，桥梁在实际运行过程中的各项指标数据均能实时上传到监控中心并由相应分析程序分析判断以得出桥梁的健康状态 [4] [5] 。对于中小型桥梁，目前因成本原因，无法完全做到实时采集数据并动态分析与判断，较多采用定期静、动载试验结合的方法分析桥梁在不同状态的受力与变形情况，从而分析、判断桥梁的健康安全状态 [6] [7] [8] [9] [10] 。

静载试验是通过测试桥梁结构在试验荷载作用下的控制截面的应变、位移或裂缝，分析判定桥梁的状态。评定现有桥梁的实际承载能力，判断结构的安全承载能力和使用条件，从而对既有桥梁的健康状况进行评估并提出桥梁维修、加固及运营管理的要求 [11] [12] [13] [14] [15] 。本文根据某跨铁路桥梁工程的静载试验，分析了既有桥梁在不同工况下的受力、变形情况，对桥梁健康状况进行了评价。

2. 工程概况

武汉市东湖新技术开发区某跨铁路桥梁，全桥总长594 m，如图1所示。主桥采用2 × 53 m变截面箱形预应力混凝土现浇连续刚构+2×34 m等截面斜腹板预应力砼连续箱梁；引桥采用3 × 30 m + 3 × 30 m + 4 × 30 m + 4 × 30 m = 420 m等截面预应力砼连续箱梁结构。下部结构主墩采用板式墩，其余桥墩均采用门型板式墩，基础均采用钻孔灌注桩。

桥梁主要技术标准为：汽车荷载：城-A；铁路荷载(仅主桥)：中-活载；有轨电车车辆轴重(仅主桥)：不大于12.5 t。经现场普查，发现桥梁排水也附近出现较为明显的水渍现象(图2)，现拟定对该桥实施静

Figure 1. The figure of bridge appearance and profile

图1. 桥梁外观图及剖面图

Figure 2. The watermark of bridge

图2. 桥梁外观渍水图

载试验以判定桥梁健康安全状态。

2. 静载试验目的及试验内容

2.1. 静载试验目的

通过静载试验，考察桥梁结构的整体变形规律，了解结构的实际受力状态和工作状况，并与数值计算结果进行对比，从而对桥梁的整体结构的安全承载能力和使用条件做出判断，检验桥梁结构的承载能力、结构变形及正常使用状态是否满足设计要求。

2.2. 试验内容

1) 理论计算

在进行荷载试验前，首先根据桥梁结构型式、控制活荷载等参数，采用有限元软件MIDAS/civil计算本桥控制截面在各个活荷载工况下的内力。控制截面最不利活载内力计算的方法是先求出该截面的内力影响线，利用影响线并根据加载车道数和动力系数计算出该截面在控制活荷载作用下的最不利内力。再按内力(应力)等效的原则确定加载车辆参数后，得出桥梁在试验荷载(加载车辆)作用下的理论应变值和位移值，用以和加载试验实测数据进行比较，从而判断桥梁结构是否满足承载力和使用要求。分别选取2 × 53 m (连续刚构)和2 × 34 m (连续箱梁)建立有限元模型进行计算(图3)，其对应的混凝土强度等级分别为C55和C50。

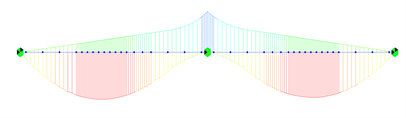
选取左幅第4联(连续刚构)和右幅第4联(连续箱梁)，采用MIDAS软件计算桥梁在控制荷载作用下的内力(弯矩)，各测试跨设计荷载标准组合弯矩包络图见图4，连续刚构对应的最大弯矩值分别16,515.5 kN∙m和−33,130.8 kN∙m，连续箱梁对应的最大弯矩值分别−8408.8 kN∙m和13,521.4 kN∙m。

(a)连续刚构 (b)连续箱梁

Figure 3. The finite element model

图3. 有限元模型图

(a)连续刚构 (b)连续箱梁

Figure 4. Design load standard combined bending moment envelope

图4. 设计荷载标准组合弯矩包络图

2) 测试截面选取及测试点布置

根据弯矩包络图，为反映桥梁在试验荷载作用下应力、挠度的大小，试验跨及测试截面详见图5，测试内容如表1所示。

Table 1. Main test section, control internal force and the test content

表1. 主要测试截面、控制内力及测试内容

考虑到测试跨的结构形式和受力特点，选取桥梁跨中截面、支点附近截面作为控制截面，测量跨中截面在各级试验荷载作用下应力及竖向变位，各截面测点布置如图6所示；测量支点截面在各级试验荷载作用下应力。

3) 试验荷载工况

根据等效荷载的原理，即设计荷载与试验荷载(载重汽车)作用效应一致的原则，并根据《公路桥梁荷载试验规程》(JTG/T J21-01-2015)规定 [16] ，对交(竣)工验收荷载，荷载试验效率宜介于0.85~1.05之间的要求，通过软件计算得出加载车吨位和台数。本次荷载试验各工况采用3~6辆载重汽车进行加载，加载车辆前轴重100 kN，后轴重400 kN，总轴重500 kN。

Figure 5. The test section of main girder stress and deflection (unit: cm)

图5. 主梁应力、挠度测试截面(单位：cm)

Figure 6. The arrangement of measuring points for stress and deflection

图6. 应力、挠度测点布置示意图

根据前面计算结果，本次桥梁结构选取三种工况状态分析结构状态，工况一对应连续刚构中的A-A、B-B截面的受力与变形，平面加载位置如图7中(a)所示，工况二对应连续箱梁中的C-C、D-D截面的受力与变形，平面加载位置如图7中(b)所示，工况三对应连续刚构中的A-A、B-B截面的最大中载正弯矩和最大中载负弯矩，平面加载位置如图7中(c)所示。

根据《公路桥梁荷载试验规程》(JTG/T J21-01-2015)规定，对交(竣)工验收荷载，荷载试验效率宜介于0.85~1.05之间的要求。

$0.85\le \eta =\frac{S_S}{S\left(1+\mu \right)}\le 1.05$ (式2.1)

式中： $\eta$ ——静力试验荷载效率；

$S_S$ ——静载试验荷载作用下控制截面内力计算值；

$S$ ——设计标准活荷载不计冲击作用时产生的某试验工况的最不利计算效应值；

$\left(1+\mu \right)$ ——设计计算取用的动力增大系数。

本次荷载试验各工况荷载效率见表2。

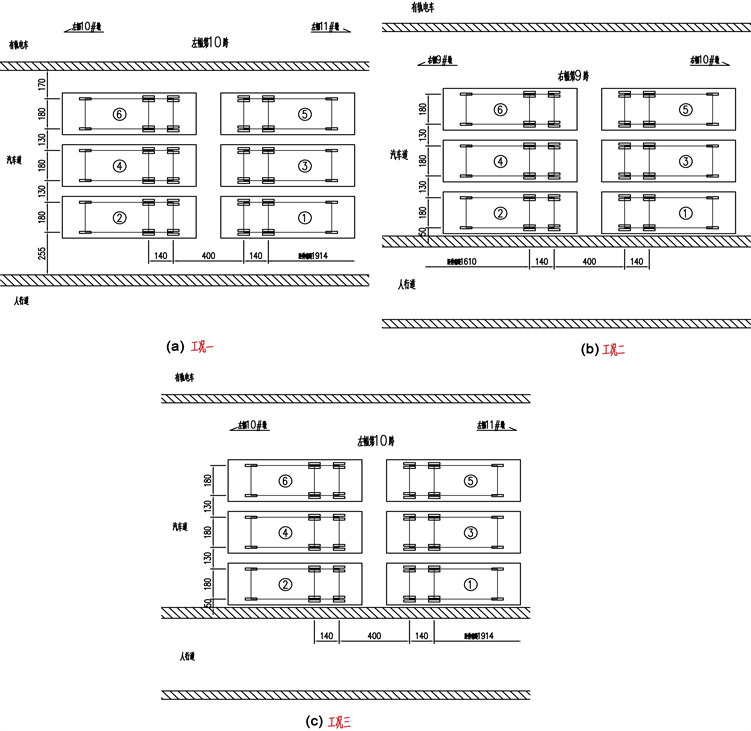
Figure 7. The position for loading (unit: cm)

图7. 平面加载位置(单位：cm)

Table 2. The efficiency of static load test load

表2. 静载试验荷载效率

注：设计控制内力已计入冲击系数(冲击系数按2004《桥规》进行计算)。

3. 测试数据分析

3.1. 实测数据计算

3.1.1. 实测挠度与应变计算

跨中截面在静力荷载试验时的挠度，按下式进行计算：

$S=D-\left(D_1+D_2\right)/2$ (式3.1)

式中：S — 桥梁某工况跨中截面在静力荷载试验时的挠度；

D — 该工况作用下跨中实测竖向变位值；

D₁ — 该工况作用下一端支座处竖向变位值；

D₂ — 该工况作用下另一端支座处竖向变位值。

静力荷载试验的各测点实测变位与应变的计算按下式进行。

1) 总变位(或总应变)：

$S_t=S_I-S_i$ (式3.2)

2) 弹性变位(或弹性应变)：

$S_e=S_I-S_u$ (式3.3)

3) 残余变位(或残余应变)：

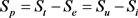(式3.4)

式中：S_i — 加载前测值；

S_I — 加载达到稳定时测值；

S_u — 卸载后达到稳定时测值。

3.1.2. 测点实测应力计算

1) 在单向应力状态下，测点应力可按下式进行计算：

$\sigma =E\epsilon$ (式3.5)

式中：σ — 测点应力；

E — 构件材料的弹性模量；

ε — 测点实测应变值。

2) 在主应力方向已知的平面应力状态下，测点应力可按《公路桥梁荷载试验规程》(JTG/T J21-01-2015)规定进行计算。

3.1.3. 主要测点的校验系数及相对残余变形的计算

对加载试验的主要测点(即控制测点或加载试验效率最大部位测点)按下式计算校验系数ζ：

$\zeta =S_e/S_s$ (式3.6)

式中：S_e—试验荷载作用下量测的弹性变位(或应变)值；

S_s—试验荷载作用下的理论计算变位(或应变)值。

对加载试验的主要测点，按下式计算其相对残余变位(或应变)：

${S^{\prime }}_P=\left(S_P/S_t\right)\times 100\%$ ； (式3.7)

式中： ${S^{\prime }}_P$ ——相对残余变位(或应变)，S_P、S_t见公式(4)、公式(2)。

3.2. 试验结果及分析

3.2.1. 挠度测试结果及分析

在各试验荷载工况作用下，连续刚构及连续箱梁测试截面竖向挠度测试结果见图8，图中工况一及工况三对应跨中A-A截面挠度，工况二对应跨中D-D截面挠度，图中各测点挠度均为负值，表明加载时各测加载时实际向下变形，在不同工况下，A-A截面及D-D截面的最大变形均发生在截面中部，测试截面在各荷载工况作用下的挠度值均小于规范规定的L/600，满足规范要求。根据前述加载量计算得到A-A、D-D截面挠度理论计算值分别为−2.52 mm和−3.01 mm，据式3.6可以计算得到A-A截面在工况一和工况三两种加载形式下的校验系数分别为0.69和0.71，D-D截面的校验系数为0.58，A-A、D-D截面均能满足校验系数要求。

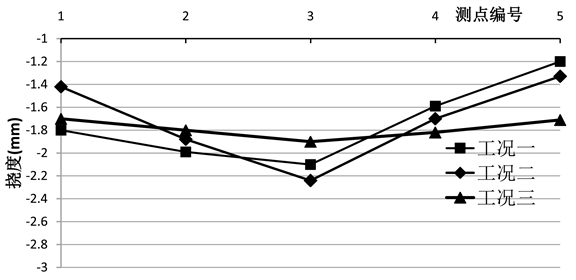
Figure 8. Deflection value under different working conditions

图8. 不同工况下各测点挠度值

在不同加载工况下，根据式3.7计算得到各测试截面在荷载试验载重汽车退出桥跨后的挠度残余变形详见表3。

Table 3. The main residual deformation value under corresponding working conditions (mm)

表3. 主桥在对应工况作用下残余变形值(mm)

测试结果表明试验跨各测试截面的残余变形均小于《公路桥梁荷载试验规程》(JTG/T J21-01-2015)的规定，满足规范要求，试验跨各主要受力构件在试验荷载作用下具有良好的弹性恢复能力。

3.2.2. 应变测试结果及分析

各测试截面在最不利试验荷载工况作用下，各测点应力测试结果及分析见图9至图11，其中，残余应变值按式3.8计算得到，图9和图10分别为A-A截面和B-B在工况一和工况三情况下的应变值及残余应变值，图11为C-C和D-D截面在工况二情况下的应变值及残余应变值。应力符号定义为：正值(+)表示拉应力，负值(−)表示压应力；图中实测值及理论值均为满载工况下应力值。

Figure 9. Measured strain and residual strain values of A-A section

图9. A-A截面实测应变及残余应变值

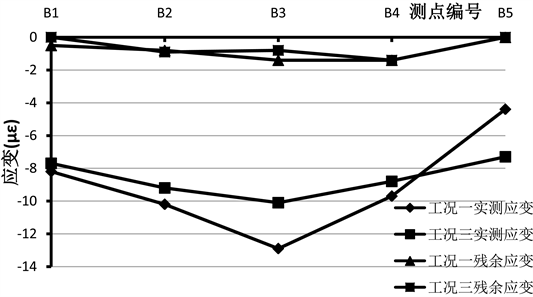
Figure 10. Measured strain and residual strain values of B-B section

图10. B-B截面实测应变及残余应变值

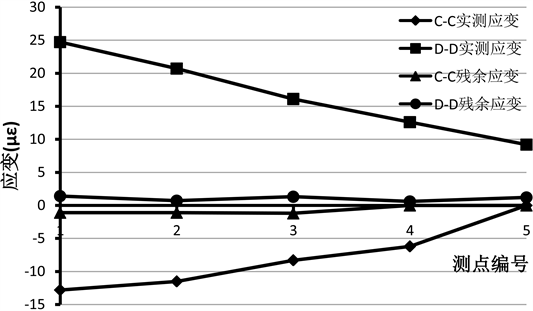
Figure 11. Measured strain and residual strain values of C-C section and D-D section

图11. C-C、D-D截面实测应变及残余应变值

A-A截面在工况一及工况三下，理论计算应变值为17，根据图9所得数据，可计算工况一、工况三对应的校验系数分为0.63及0.59；B-B截面在工况一及工况三下，理论计算应变值为−13，根据图10所得数据，可计算工况一、工况三对应的校验系数分为0.7及0.66；在工况二下，C-C、D-D截面对应理论计算应变值分别为−18及30，实测数据分析得到对应的校验系数分别为0.54和0.56。各测试截面在试验工况荷载作用下，各截面的正应力校验系数为0.54~0.75 (<1.0)。根据《公路桥梁荷载试验规程》(JTG/T J21-01-2015)规定，说明各试验跨强度满足设计荷载等级的正常使用要求。

各测试截面在荷载试验载重汽车退出桥跨后的残余应力最大值为1.5，对应的相对残余应变最大值为0.15，小于规范容许值0.2，因此，各截面残余应力均能满足要求。表明试验跨各主要受力构件在试验荷载作用下具有良好的弹性恢复能力。

4. 结论

1) 测试截面在各荷载工况作用下的挠度值均小于规范规定的L/600，满足规范要求，试验跨跨中截面的挠度校验系数在0.58~0.75之间，校验系数均小于1，依据《公路桥梁荷载试验规程》(JTG/T J21-01-2015)，说明本桥试验跨满足设计荷载等级正常使用要求。

2) 各测试截面在试验工况荷载作用下，各截面的正应力校验系数为0.52~0.75 (<1.0)。根据《公路桥梁荷载试验规程》(JTG/T J21-01-2015)规定，说明各试验跨强度满足设计荷载等级的正常使用要求。

3) 试验跨各测试截面的残余变形和残余应变均小于《公路桥梁荷载试验规程》(JTG/T J21-01-2015)的规定，满足规范要求，试验跨各主要受力构件在试验荷载作用下具有良好的弹性恢复能力。

NOTES

^*通讯作者。