关于有效应力定理预测地层压力的几个问题

Some Problems about Pore Pressure Prediction from Effective Stress Theorem

摘要: 地层压力预测在石油勘探和开发中是一项非常重要的工作，关于地层压力预测理论和方法的应用存在一些疑问和误解。本文就Terzaghi (1923)和Biot和Williss (1957)提出的有效应力定理中各参数的物理含义和地质含义进行了全面的分析，并且指出了当前地层压力存在的问题和难点，总结了钻前压力预测和钻后压力预测的用途和意义，对进一步提高压力预测精度具有重要的参考价值。

Abstract: Pore pressure prediction is a very important task in oil exploration and exploitation, and there are some doubts and misunderstandings about the application of theory and method of pore pressure prediction. In this paper, the physical and geological meanings of the parameters in the effective stress theorem presented by Terzaghi (1923) and Biot and Willis (1957) are comprehensively analyzed, and the existing problems and difficulties of pore pressure are pointed out. The purpose and significance of pre-drilling pore pressure prediction and post-drilling pore pressure prediction are summarized, which will enhance the pore pressure prediction accuracy further and are referable for oil exploration and exploitation.

1. 引言

有效应力定理具有广泛的用途，普遍应用于矿山开发、隧道工程、堤坝建设和石油勘探开发中，是岩土力学中的一个非常重要的理论。尽管有效应力定理被人们普遍使用和接受，但是几十年来关于有效应力定理的质疑声一直不断，特别是在石油勘探开发中，关于有效应力定理的应用存在一些疑问和误解。

Terzaghi (1923)根据实验室测量(图1)，提出含水饱和土壤的有效应力定理，土壤在应力条件下的应变和破坏取决于压力差(有效应力) [1]

$P_p=P_c-P_d$ (1)

式中：P_c是围压，P_p是孔隙流体压力，P_d是压力差(有效应力)。

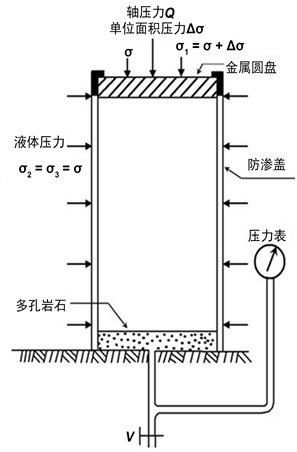
Figure 1. The triaxial compression testing device (Terzaghi, 1923)

图1. 三轴压缩测试装置(据Terzaghi, 1923) [1]

图1中展示了一个饱和黏土竖直圆柱样品，其顶部被金属圆盘覆盖，其底部被多孔岩石托着，避免样品与排水阀门V直接相连，防止黏土在施压状态下通过阀门漏出。

Biot (1941)建立了饱含水固结黏土的三维力学模型，模型中的参数比较抽象，不是很明确 [2] 。后来Biot和Willis (1957)基于低渗透性多孔介质(例如岩石)提出了修正后的有效应力定理，由此引入有效应力系数的定义 [3] ，即

$\begin{array}{l}n{P}_p=P_c-P_e\\ n=1-\frac{K_{dry}}{K_{ma}}\end{array}\}$ (2)

式中：P_c是围压，P_p是孔隙流体压力，P_e是有效应力。K_dry为多孔干燥岩石的体积模量(排水状态下的体积模量)，K_ma为岩石基质的体积模量，n是有效应力系数(也称为Boit或Biot-Willis系数，有的文献中用α表示有效应力系数)。Nur和Byerlee (1971) [4] 从理论和实验测试手段证实了Biot和Willis (1957) [3] 提出的有效应力定理的有效性，在这里需要强调的是，Biot和Willis (1957) [3] 的有效应力定理描述了饱和多孔岩石在孔隙压力保持不变的情况下岩石应变与应力的关系，不能解释饱和岩石孔隙压力随着围压增加而增加的力学机制。事实上，Biot和Willis (1957) [3] 提出的有效应力定理式(2)包含了Terzaghi (1923) [1] 提出的有效应力定理式(1)，地面疏松干燥的多孔土壤的体积模量K_dry往往远小于土壤颗粒的体积模量K_ma。Sarker和Batzle (2008)的研究也证实在较浅的地层中K_dry $\ll$ K_ma，n ≈ 1；因此在较浅的地层中上述式(2)可简化为式(1) [5] 。

Zimmerman (1991)从二维力平衡的角度推导出岩石基质的平均应力(有效应力)表达式(图2) [6]

$P_c=\left(1-\varphi \right)\bar{P}+\varphi P_p$ (3)

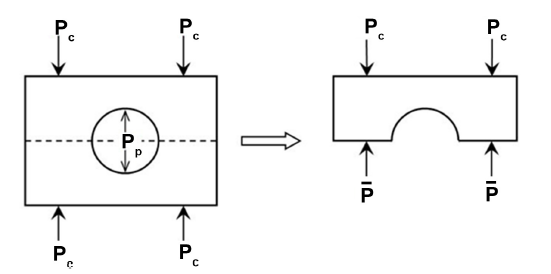
Figure 2. Force-balance argument for the derivation of the mean-stress relationship (Zimmerman, 1991)

图2. 用于推导平均应力关系的力平衡原理(据Zimmerman, 1991) [6]

式(3)在实践应用中很少见，其主要原因是式(3)是一个二维力平衡理论模型，难以解释三维应力状态下岩石的力平衡状态。

在石油勘探开发实践中，最常用的是Terzaghi (1923)提出的有效应力定理，而Biot和Willis (1957)提出的有效应力定理大多情况下以理论的形式存在。在Terzaghi (1923)的有效应力定理中，孔隙流体压力P_p等于岩石所承受的围压P_c与岩石骨架(相当于排水状态下的岩石)所承受的有效应力P_d之差；Biot和Willis (1957)的有效应力定理引入了有效应力系数n的定义，其有效应力P_e与Terzaghi (1923)的有效应力定理中P_d有差别。根据前人的研究结果和长期地层压力预测研究工作，现对有效应力定理预测地层压力容易含糊的几个问题进行剖析。

2. 围压P_c

目前在石油勘探开发中，人们对Terzaghi (1923) [1] 和Biot和Willis (1957) [3] 提出的有效应力定理作了大的简化。事实上，Terzaghi (1923) [1] 和Biot和 Willis (1957) [3] 提出的有效应力定理式(1)和式(2)中围压P_c是指三个主应力方向的平均应力，即P_c = (σ₁ + σ₂ +σ₃)/3，而不是上覆地层压力P_ov，一般规定σ₃为上覆地层压力P_ov，σ₁和σ₂分别为两个水平主应力(有最大和最小水平主应力之分) (图3)，上覆地层压力P_ov只是三个主应力中的一个应力，有时P_c与P_ov的关系受区域构造运动的影响(图4)。

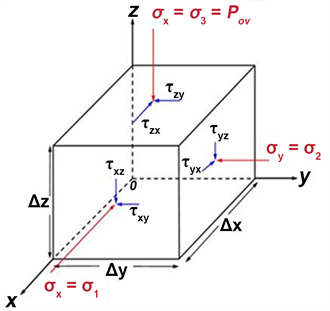
Figure 3. The diagrammatic sketch of three-dimensional stress of rock

图3. 岩石三维受力示意图

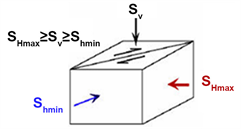
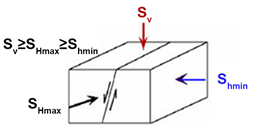正断层走滑断层 逆断层

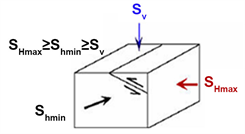
Figure 4. The three types of faults, classified according to relative magnitudes of the principal stresses (Anderson, 1942)

图4. 根据主应力相对大小关系划分的三种类型的断层(Anderson, 1942) [7]

图4中S_Hmax是最大水平主应力；S_hmin是最小水平主应力；S_v是垂直应力，可认为是上覆地层压力P_ov，围压P_c = (S_v + S_Hmax + S_hmin)/3。例如在逆推覆构造区域S_Hmax ≥ S_hmin ≥ S_v，P_c ≥ P_ov；在正断层构造区域S_v ≥ S_Hmax ≥ S_hmin，P_c ≤ P_ov；在走滑构造区域S_Hmax ≥ S_v ≥ S_hmin，P_c与P_ov的关系不确定。Zoback (2010)指出，在存在较大挤压应力或者沉积和初始压实后孔隙压力增加较大的情况下，不能利用简单压实曲线对孔隙压力进行预测 [8] 。

3. 有效应力P_e

有效应力概念来源于土力学的研究中，是指土壤在荷载作用下，通过粒间接触面传递的平均法向应力，是颗粒之间的接触应力，是一种虚拟的应力，在实践中无法进行测量 [1] 。由于组成多孔土壤或多孔岩石的颗粒排列、体积大小和几何形状是不规则的，各颗粒的有效应力一般都不相等，因此对于单位体积的土壤或者岩石而言，有效应力是指组成多孔土壤或多孔岩石颗粒的总体所承受的平均应力。Terzaghi (1923) [1] 和Biot和 Willis (1957) [3] 提出的有效应力定理式(1)中的P_d和式(2)中的P_e分别指土壤和岩石的平均有效应力，而不是垂直有效应力。事实上，对于Terzaghi (1923)的有效应力定理 [1] ，在三个主应力方向有

$\begin{array}{l}{P}_{e1}={\sigma }_1-P_p\\ P_{e2}={\sigma }_2-P_p\\ P_{e3}={\sigma }_3-P_p\end{array}\}$ (4)

对于Biot和 Willis (1957)的有效应力定理 [3] ，在三个主应力方向有

$\begin{array}{l}{P}_{e1}={\sigma }_1-n{P}_p\\ P_{e2}={\sigma }_2-n{P}_p\\ P_{e3}={\sigma }_3-n{P}_p\end{array}\}$ (5)

式(4)中P_d = (P_e1 + P_e2 + P_e3)/3，式(5)中P_e = (P_e1 + P_e2 + P_e3)/3。P_e1、P_e2和P_e3分别为相对应的三个方向的有效应力，σ₁、σ₂、σ₃和P_e1、P_e2、P_e3的区别是，σ₁、σ₂、σ₃分别是作用在岩石上三个主应力方向的力，而P_e1、P_e2、P_e3是岩石骨架三个主应力方向所承受的力(有效应力)。式(5)中垂直应力方向σ₃ = P_ov，那么

$P_{e3}=P_{ov}-n{P}_p$ (6)

在实际应用中，人们常常简化有效应力系数n = 1，那么式(6)可简化为

$P_{e3}=P_{ov}-P_p$ (7)

式(7)就是目前人们常用的地层压力预测模型，用声波速度或者地震波速度描述垂直有效应力P_e3 (表1)

$P_{e3}=f\left(V\right)$ (8)

用声波速度或者地震波速度描述垂直有效应力主要是针对页岩和泥岩而言的，一些不依赖于泥页岩欠压实理论的地层压力预测模型，声波速度或者地震波速度也仅仅只能描述单一岩性的垂直有效应力，在实际应用中这些方法预测地层压力的精度都会受到岩性的影响(见表1)。除此之外，Banik等(2013) [17] 和胡华锋等(2018) [18] 用波阻抗分别替代Bowers (1995)和Eaton (1972)模型中的纵波速度，提出了直接利用波阻抗预测地层压力的方法，其依据是密度和速度呈正相关关系，但是其本质与Bowers (1995)和Eaton (1972)模型一样，预测地层压力的精度仍然受到岩性的影响。利用有效应力定理预测地层压力，其难点和重点就是垂直有效应力的计算。就目前而言，钻前压力预测主要还是根据地震叠加速度计算层速度使用基于泥页岩欠压实理论Eaton法(Eaton, 1972) [10] 预测地层压力，主要是对地层中可能存在的异常高压进行预测，其预测结果作为石油钻井泥浆比重配备的参考依据。尽管其预测精度有限，但是地震叠加速度是目前作为钻前压力预测唯一容易得到的地层速度信息，是钻前压力预测最常用的速度资料。

4. 有效应力系数n

有效应力系数在地层压力预测中是一项非常关键的参数，有效应力系数的精确估算一直是一个难题，一直局限于实验室的测量，并没有得到广泛的应用，在地层压力估算中n经常被假设为1。Geertsma (1961) [19] 、Krief等人(1990) [20] 、Nur等人(1995) [21] 、Hilterman (2001) [22] 和马中高(2008) [23] 根据实验室测量方法，将有效应力系数n看成是孔隙度f的函数，提出了一些经验公式，但这些经验公式往往只适用于局部地区或者单一岩性，对于全区或者复杂岩性的应用，有时就受到了局限(Wang, et al. 2016) [24] 。

Table 1. Prediction method of pore pressure based on P-wave velocity

表1. 基于纵波速度的地层压力预测方法

Wang等人(2016) [24] 根据Pickett (1963)和他人的实验结果 [25] ，干燥岩石的泊松比常常近似地等于矿物的泊松比，或K_dry/K_ma = μ_dry/μ_ma (Mavko et al. 1998, p. 244) [26] 的关系联立Biot-Gassmann 原理(Gassmann, 1951 [27] ; Biot, 1956 [28] )推导出一种新的估算有效应力系数的方法。

$\begin{array}{l}a{K}_{ma}^2+b{K}_{ma}+c=0\\ a=\frac{\varphi }{K_f}\left(K_{sat}+\frac{4}{3}{\mu }_{sat}\right)-1\\ b={\rho }_{ma}{V}_{ma}^2\left(1-\frac{\varphi K_{sat}}{K_f}\right)+\left(1-\varphi \right)K_{sat}-\frac{4}{3}\left(1+\varphi \right){\mu }_{sat}\\ c=K_{sat}\left(\frac{4}{3}{\mu }_{sat}-{\rho }_{ma}{V}_{ma}^2+\varphi {\rho }_{ma}{V}_{ma}^2\right)\\ K_{ma}=\frac{-b+\sqrt{b^2-4ac}}{2a}\\ \frac{K_{dry}}{K_{ma}}=\frac{\frac{K_{sat}}{K_{ma}}\left[1+\varphi \left(\frac{K_{ma}}{K_f}-1\right)\right]-1}{\frac{K_{sat}}{K_{ma}}+\left[1+\varphi \left(\frac{K_{ma}}{K_f}-1\right)\right]-2}\end{array}\}$ (9)

式中：a，b，c是方程的系数，ρ是饱和岩石的体积密度， $\varphi$ 是岩石的孔隙度，K_sat是饱和岩石体积模量，μ_sat是饱和岩石的剪切模量，K_f 是孔隙流体体积模量，V_p和V_s分别是岩石的纵波速度和横波速度，ρ_ma为岩石基质的体积密度，V_ma是岩石基质的纵波速度。在式(9)中通过估算岩石基质体积模量的新方法，由Gassmann方程 [27] 计算干燥岩石体积模量K_dry和岩石基质体积模量K_ma的比值来求取多岩性有效应力系数n。式(9)估算岩石的有效应力系数，不受区域限制，不受岩性影响，适用于多岩性的有效应力系数的估算。

Norris (1989)给出了有效应力系数的一般边界为 [29]

$\frac{3\varphi }{2+\varphi }\le n\le 1$ (10)

由于 $3\varphi /\left(2+\varphi \right)$ 总是超过孔隙度 $\varphi$ 一个有限的量，当 $\varphi$ 大于零时，n总是大于 $\varphi$ 。Wang 等人 (2016) [24] 的计算结果也证实了Norris (1989)的结论是有效的 [29] 。在两种极端情况下：1) 当孔隙度 $\varphi =0$ 时，K_dry = K_ma，n = 0为固结良好的沉积岩、致密的沉积岩。2) 当孔隙度φ ≥ φ_crit (φ_crit为临界孔隙度)时，K_dry = 0，n = 1为未固结的沉积物或流体，因此0 ≤ n ≤ 1 (Hilterman, 2001) [22] 。

5. 孔隙流体压力P_p

地层压力又称地层孔隙流体压力，是指地层孔隙流体所承受的压力，分为正常地层压力、异常低地层压力和异常高地层压力。王鸿升(2016)对异常高地层压力研究现状进行了概述 [30] ，对比了国内外异常高地层压力成因(见表2)。其实关于异常高地层压力成因国内与国外的分类本质上是一样的，比如说沉积成岩型主要是地层的压实作用(如欠压实，也称为不平衡压实)产生异常高地层压力，与岩石孔隙体积的变化相对应。成烃型主要是生烃作用，导致流体膨胀产生异常高地层压力，与孔隙流体体积变化相对应。构造型主要指由构造应力场的作用导致围压额外增加引起孔隙流体超压。流体压力(水压头)的变化及流体运动引起的孔隙流体超压在油藏的开发过程中表现尤为明显，往油藏中注水，往往能增加油藏的地层压力。不过，国内学者在异常高地层压力的分类上提出了非渗透性地层超压和渗透性地层超压的观点，这种观点对地层压力的预测研究非常重要。Shaker (2002)认为，目前地层压力的术语可能被混淆了，预测的地层压力是那些相对不渗透地层(页岩和泥岩)的孔隙流体压力，而实际测量的地层压力却是储层特性岩石

Table 2. Comparison of genesis of abnormal high pressure both at home and abroad

表2. 国内外异常高地层压力成因对比

(砂岩)的孔隙流体压力。然而在很多情况下，砂岩孔隙中的压力与页岩夹层的压力没有直接的关系，假如存在直接的关系，可能会导致严重的钻井事故。因为超压页岩中的砂岩目的层压力可能比周围页岩低，稍有不慎，就有可能由于过重的补偿泥浆将砂岩压漏。预测的地层压力和测量的地层压力之间的关系是非常复杂的，涉及到地质背景的分析和烃类的预测 [40] 。而Shaker (2002) [40] 指出了目前地层压力预测最根本的问题，如一些基于泥岩或页岩欠压实理论的方法，预测的是泥岩或页岩的孔隙流体压力(非渗透性地层压力)，而实际测量的是储层类岩石(如砂岩)的孔隙压力(渗透性地层压力) (王鸿升，2016) [30] 。这就涉及到岩石的孔隙是否连通的问题，如果岩石的渗透率接近于零，岩石中的各孔隙互相不连通(图5)，那

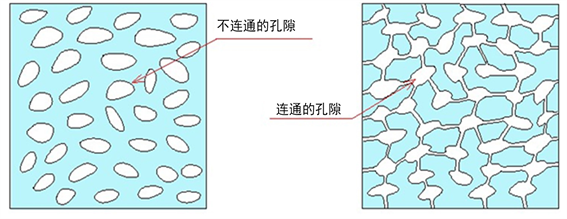
Figure 5. The porous rock model of disconnected pore and connected pore

图5. 不连通孔隙与连通孔隙岩石模型

么孔隙流体的压力如何来描述呢？问题的根源在于，多孔岩石在非渗透性的情况下，岩石孔隙流体的压力是无法直接测量的。不过根据有效应力系数的定义来讲，当岩石的孔隙度φ = 0时，有效应力系数n = 0，根据式(2)可得，孔隙流体压力P_p = 0，上覆地层的静岩压力全部被岩石基质所承担，因为没有孔隙，顾名思义就不存在孔隙流体压力了，但是岩石的渗透率为零，不代表岩石的孔隙度为零，有孔隙存在但孔隙不连通，渗透率也能为零。

Biot和Willis (1957) [3] 提出的修正后的有效应力定理式(2)是否适用于非渗透性地层的孔隙流体压力计算，到目前没有一个肯定的结论。在一般情况下，泥岩和页岩的渗透率很低，可接近于零。Mitchel指出结合水的结构不同于一般水，但结合水在水动力特性与一般水没有本质的区别，达西定律还是适用的 [41] 。李广信(2011)通过实验室测量发现，黏性土结合水是能传递水压力的,但是其力学机制难以从应变与应力的关系来进行解释 [42] 。

6. 结论

有效应力定理(Terzahi, 1923 [1] ; Biot和Willis, 1957 [3] )揭示了多孔弹性材料中多孔骨架与孔隙流体分担围压的力学机制，这一理论主要是建立在孔隙压力保持不变的情况下岩石应变与应力的关系，不能解释饱和岩石孔隙压力随着围压增加而增加的力学机制。沉积岩在压实成岩过程中孔隙压力随着围压增加而增加，因此现有有效应力定理理论上存在缺陷。

地层压力预测对于石油钻井安全尤为重要，根据目前的理论和方法，仅用纵波速度不能全面的预测井下地层连续的压力分布。井位完钻后，如能根据测井资料估算更为精确的地层压力可提高地应力的估算精度，在油藏工程方面具有重要的应用价值。因此在石油勘探和开发中，最好是对钻前压力预测和钻后压力估算采取不同的对策，结合地质背景，针对具体问题具体分析，从理论和方法技术上综合形成一套压力预测方案。

基金项目

国家科技重大专项课题“陆相页岩油甜点地球物理识别与预测方法”(2017ZX05049-002)和胜利油田分公司课题“地震低频油气判识技术研究——以垦东北为例”(YKW1705)联合资助。

参考文献