1. 引言
天然气水合物，是水和天然气在低温高压下形成的晶体状固态混合物，其沉积物是指含水合物的天然土体。作为一种新型能源，天然气水合物清洁无污染、燃烧放热量大，1 m3水合物相当于164 m3的天然气燃烧释放的热量 [1] ，是世界各国研究开采的重点。目前水合物开采工艺尚不成熟，且水合物储层复杂，开采环境恶劣，开发过程中储层极易坍塌。因此研究水合物沉积物的力学性质对于保证水合物的安全开采具有重要意义 [2] 。
目前国内外已有众多学者对水合物沉积物进行研究，加深了人们对于水合物沉积物力学性质的认识。但水合物在土壤中的赋存条件苛刻，采集水合物沉积物原状试样所需设备昂贵，且相关的试验技术不成熟，试验研究存在极大困难。因此许多学者选择通过人工合成水合物或者似水合物的方式来进行室内试验研究。Soga等 [3] [4] [5] 通过在低于冰点的砂子和细冰粒的混合物中人工合成水合物，研究了水合物沉积物的强度以及其他力学参数与饱和度的量化关系；Hyodo等 [6] [7] 利用冰–砂混合物和水–砂混合物与天然气形成两种不同类型的水合物沉积物，研究了不同形成方法、温度、有效围压以及水合物分解等对沉积物强度及变形特性的影响。然而室内试验无法对水合物沉积物力学性质的各项影响因素进行单独探讨，限制了水合物沉积物复杂力学性质的系统研究。
颗粒流方法 [8] 因其在计算混合体材料以及表现岩体的几何特点等方面的巨大优势，在岩土问题研究应用中愈加广泛，成为研究这类问题的有力工具。Brugada等 [9] 利用颗粒流软件对两种不同生成顺序的水合物沉积物进行了三轴压缩模拟，并对两种不同生成顺序的试样对比分析水合物沉积物的力学特性；Jung等 [10] 模拟了两种赋存方式的水合物沉积物，分析了不同类型水合物沉积物的应力应变关系及微观力链网络的差异；Masui等 [11] 使用颗粒流软件对砂土颗粒介质进行双轴压缩试验的数值模拟，从速度场、位移场、转动场以及力链网络等4个方面对砂土颗粒介质体系剪切带的形成与演化过程和机理进行了详细的分析；杨期君等 [12] 利用“半径膨胀法”生成不含水合物的沉积物试样，然后计算满足所需饱和度的水合物颗粒数目，并将水合物颗粒在土颗粒孔隙中随机填充，再使所有颗粒经过充分运动达到平衡，最后得到所需饱和度的水合物沉积物试样；蒋明镜等 [13] [14] [15] [16] 考虑水合物对土颗粒的胶结作用，用平行胶结模型将多个水合物颗胶结在一起生成水合物团簇，从而模拟沉积物中水合物的破坏。上述研究为水合物沉积物力学性质的研究提供了新思路，有助于人们了解其复杂力学性质，但建模过程繁琐、复杂，并不能很好地反映水合物沉积物的实际情况。
为了有效利用颗粒流方法对水合物沉积物力学性质进行模拟分析，本文采用同时生成土体–水合物两种类型颗粒并赋予线性接触的方式制备不同饱和度水合物沉积物颗粒组构模型试样，研究饱和度及围压对水合物沉积物强度特性的影响，研究结果可为水合物开采所涉及的井壁失稳、地层变形等工程问题提供基础力学参数和技术参考。
2. 水合物沉积物颗粒组构模型试样制备
构建有效反映材料细观结构的颗粒组构模型试样，是进行数值模拟分析的前提与基础。根据Waite等 [17] 对水合物存在模式的分类：当水合物饱和度Sh < 25%时，水合物在沉积物孔隙中，为孔隙填充型水合物；当水合物饱和度25% < Sh < 40%时，孔隙填充型水合物转变为骨架支撑型水合物。
本文基于颗粒流软件提出了一种制备水合物沉积物的颗粒组构模型试样方法，建立0%、10%、20%、30%和35%五种饱和度水合物试样，制备流程如图1所示。
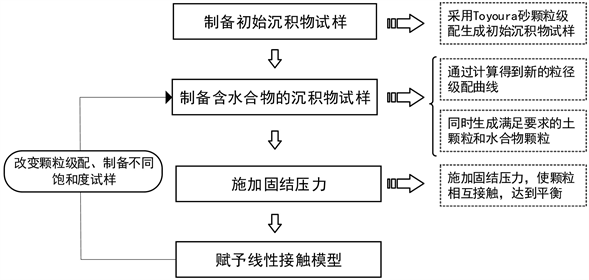
Figure 1. Flow chart for preparing particles arranged model samples of hydrate sediment
图1. 水合物沉积物颗粒组构模型试样制备流程
首先采用图2所示的Toyoura砂粒径级配生成初始孔隙比为0.42，直径2 mm，高度4 mm的不含水合物的初始沉积物圆柱体试样，模拟土颗粒的圆球颗粒直径为0.1~0.4 mm。然后将水合物颗粒的粒径设置为一较小的定值，设定土颗粒粒径的取值范围，根据饱和度、初始孔隙率及初始粒径级配曲线，计算新的孔隙率及粒径级配曲线，再按照满足饱和度和孔隙度要求的粒径级配曲线同时生成土颗粒和水合物颗粒。因为水合物是在沉积物的孔隙中形成，试样中的水合物颗粒直径应较小，根据计算经验，本文的水合物颗粒直径取为0.06 mm。接下来对试样施加一定的固结压力(本文取0.5 MPa)，使颗粒在固结压力下相互接触，达到平衡。最后将线性接触模型赋予生成的不同饱和度的沉积物颗粒组构模型试样。
本文材料参数中的密度和摩擦系数采用南海海槽的数据 [11] ，颗粒的法向刚度根据其粒径变化保持接触模量为常数，如表1所示。
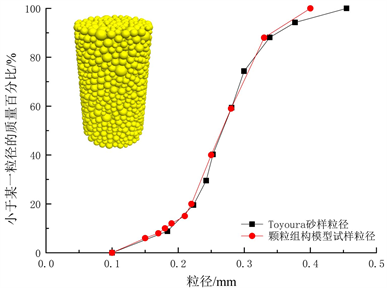
Figure 2. Grain gradation curve and particles arranged model specimen
图2. 颗粒级配曲线与颗粒组构模型试样
Table 1. Sample parameters of Particle Flow Code simulation
表1. 颗粒流模拟中的接触以及材料参数
最终制成的饱和度为10%、20%、30%和35%的水合物沉积物颗粒组构模型试样图和接触图如图3所示，其中黄色颗粒为土颗粒，蓝色颗粒为水合物颗粒，红色为颗粒间的接触。当水合物饱和度较低时，沉积物中颗粒接触较少，水合物颗粒对沉积物试样不起胶结作用；当水合物饱和度较高时，沉积物中颗粒接触显著增加，水合物颗粒使土颗粒胶结，使沉积物试样的强度提高。
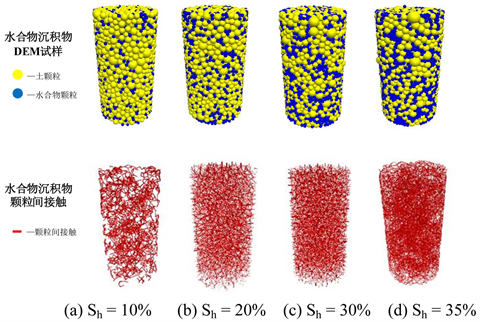
Figure 3. Particles arranged model samples and contacts of hydrate sediment in different saturations
图3. 不同饱和度下的水合物沉积物颗粒组构模型试样和颗粒间接触
3. 三轴压缩模型验证
为研究水合物沉积物的力学性质，对不同饱和度、围压下的水合物沉积物试样进行了一系列假三轴压数值模拟试验。试验流程为：利用PFC3D的伺服控制技术使整个试样保持恒定围压，通过上、下墙体的移动对颗粒组构模型试样加载进行三轴压缩数值模拟实验，加载过程对上、下墙体速度采取逐级增加的方式。
本文颗粒流数值模拟曲线和Brugada等 [9] 水合物沉积物试样的试验曲线对比如图4所示。饱和度为20%时，本文的颗粒流数值模拟曲线和Brugada等模拟结果取得较好的一致，本文模拟的剪切峰值强度是1.57 MPa，Brugada等模拟结果剪切峰值强度是1.54 MPa，误差为1.9%。因此本文的颗粒组构模型数值成样方法能有效反映水合物沉积物的特点，可用来进行水合物沉积物的力学性质分析。
4. 计算结果分析
4.1. 应力应变
不同水合物饱和度(Sh = 0%，10%，20%，30%和35%)沉积物颗粒组构模型试样在1 MPa围压下的应力–应变关系如图5所示，曲线大致可分为四个阶段：第I阶段是弹性阶段，曲线为偏离纵轴的斜直线，偏应力随着轴向应变的增大近似直线增加；第II阶段是弹塑性阶段，随着曲线斜率的减小，偏应力达到了峰值；第III阶段水合物沉积物表现出软化现象，偏应力迅速下降并趋于稳定的值，试样发生破坏；第IV阶段显示了水合物沉积物试样的残余强度，残余应力以几乎恒定的速率变化，直到三轴压缩试验结束。
计算结果表明：饱和度是影响水合物沉积物力学性质的重要因素。随着水合物饱和度的增加，沉积物试样表现出明显的应变软化现象。沉积物试样的剪切强度(最大偏应力)随水合物饱和度的增大而增大，剪切强度主要是由颗粒–颗粒之间的相互作用，当水合物饱和度从Sh = 0%增加到Sh = 35%时，剪切强度从1.40 MPa增加到1.88 MPa；在加载的初始阶段，沉积物试样的偏应力随着轴向应变增大而近似线性增大，宏观弹性模量随着饱和度增加而增大，由于水合物的存在，沉积物试样的强度得到提高。
4.2. 体积应变
图6给出了不同水合物饱和度在围压为1 MPa下的体积应变和轴向应变的关系曲线。图中曲线表明，水合物饱和度从Sh = 0%增大到Sh = 35%时，水合物沉积物试样的体积压缩量变化较小，水合物沉积物颗粒组构模型试样表现出先体积压缩后体积膨胀的趋势，并且体积膨胀现象随着饱和度的增加而愈发明显。在相同的土颗粒中填充不同体积的水合物颗粒，所填充的水合物颗粒数目越多，土颗粒间的孔隙就会越少。随着轴向应变的增加，水合物和土颗粒间的接触会逐渐破坏，土颗粒和水合物颗粒通过颗粒间的挤压和错动来调整所处位置，从而水合物沉积物试样表现出体积膨胀的现象，饱和度越高，现象越明显。
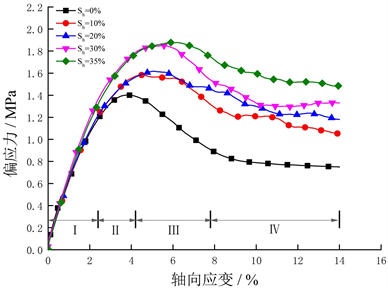
Figure 5. Effect of hydrate saturation (Sh) on stress-strain relationship
图5. 不同饱和度下沉积物的应力–应变关系曲线
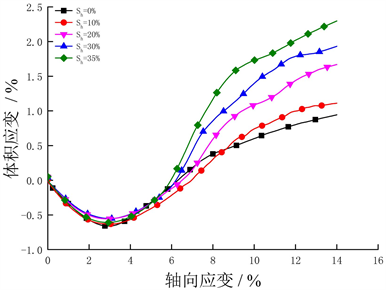
Figure 6. Effect of hydrate saturation (Sh) on volumetric response
图6. 不同饱和度下沉积物的体积应变关系曲线
4.3. 围压对水合物沉积物力学性质的影响
考虑围压对沉积物试样力学性质的影响，图7为水合物饱和度为20%时三种不同围压下体积应变的变化。结果表明，随着围压的增加，水合物沉积物体积应变近似线性增加，当围压从1 MPa增加到3 MPa，最大体积应变增加约300%。图8为不同围压下最大压缩体积应变与水合物饱和度的关系图。一般来说，最大压缩体积应变随着水合物饱和度的增加而减少，但减少量不大。可见在低饱和度时，水合物饱和度的改变对沉积物试样的内部结构影响不大，水合物的对沉积物试样并不能起到胶结作用。
图9为在不同围压、饱和度下的水合物沉积物应力应变关系。以水合物饱和度为20%的结果为例，当围压从1 MPa增加到3 MPa时，峰值剪切强度从1.45 MPa增加到4.42 MPa，增加约300%，弹性模量从60 MPa近似线性增加到83 MPa。在相同饱和度下，水合物沉积物试样的弹性模量、峰值剪切强度均随围压的增加而增大。
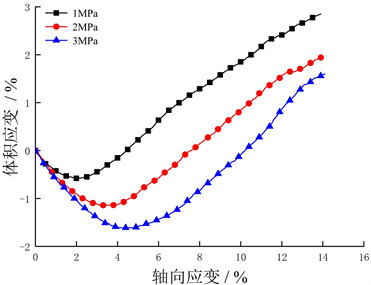
Figure 7. Effect of confining pressure on volumetric response: hydrate saturation Sh = 20%
图7. 水合物饱和度为20%不同围压下的体积应变关系图
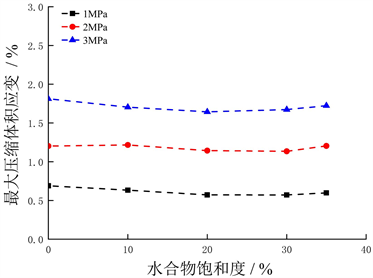
Figure 8. Maximum compressive volumetric strain vs hydrate saturation (Sh)
图8. 最大压缩体积应变与水合物饱和度的关系曲线
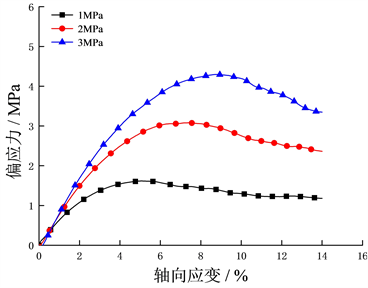(a) 水合物饱和度为10% 
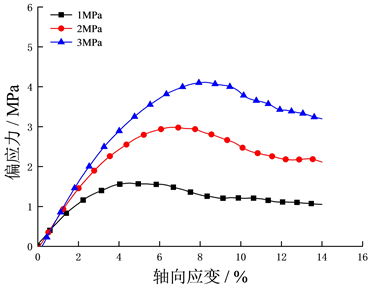(b) 水合物饱和度为20% 
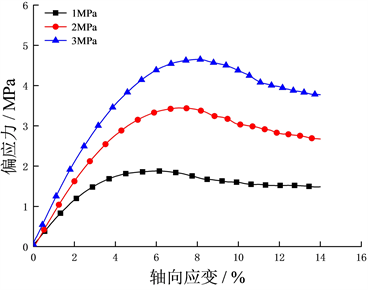(c) 水合物饱和度为30% 
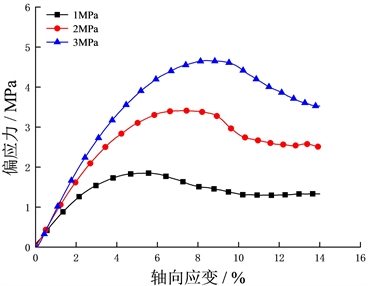(d) 水合物饱和度为35%
Figure 9. Effect of confining pressure on stress-strain relationship
图9. 不同围压下水合物沉积物的应力–应变关系图
4.4. 黏聚力与内摩擦角
根据图9不同围压时的水合物沉积物三轴压缩试验的应力应变关系，可求得不同水合物饱和度Sh沉积物试样的强度参数内摩擦角
和黏聚力
，如图10、图11所示。
水合物沉积物试样的内摩擦角随着水合物饱和度的增大而增大，当水合物饱和度为10%时，内摩擦角为22.6˚，水合物饱和度增加为35%时，内摩擦角为32.6˚，近似线性增大。而试样的黏聚力变化趋势平缓，这与Brugada等 [9] 开展的孔隙填充型沉积物特性相符合，即对于低水合物饱和度沉积物试样，水合物对于试样力学特性的贡献主要是摩擦特性而非胶结特性。
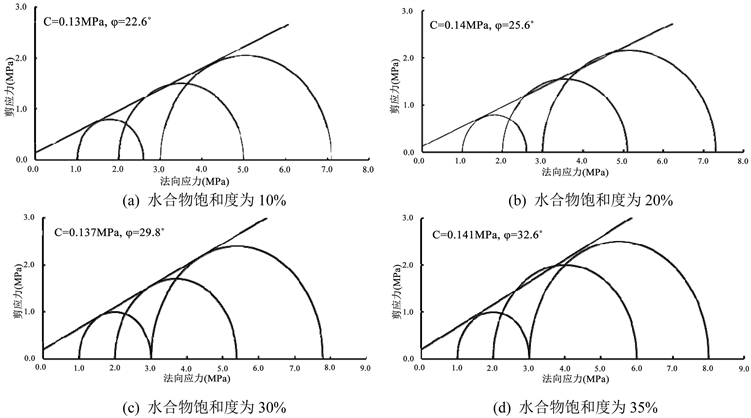
Figure 10. Mohr-coulomb failure diagram under different saturation
图10. 不同水合物饱和度的摩尔圆曲线
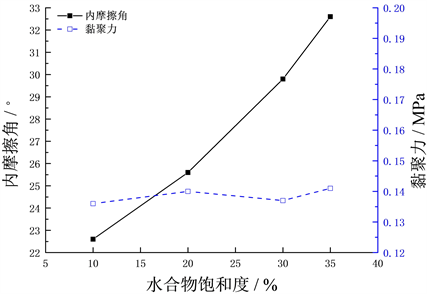
Figure 11. Variation of friction angle and cohesion vs hydrate saturation (Sh)
图11. 水合物沉积物的内摩擦角和粘聚力水随合物饱和度的变化关系曲线
5. 结论
本文基于颗粒流理论，采用同时生成土体–水合物两种类型颗粒并赋予线性接触的方式制备不同饱和度水合物沉积物颗粒组构模型试样，通过模拟三轴压缩试验来研究不同饱和度水合物沉积物的力学特性。
主要结论如下：
1) 饱和度是影响水合物沉积物力学性质的重要因素。水合物的存在提高了沉积物的强度，饱和度越高，水合物沉积物的强度越大、应变软化现象明显。在三轴压缩试验中，水合物沉积物会出现先体积压缩后体积膨胀的趋势，且随着饱和度的增加而愈发明显；
2) 围压对水合物沉积物力学性质的影响较大。在相同饱和度下，水合物沉积物试样的弹性模量、剪切强度、体积应变、最大压缩体积应变均随围压的增加而提高，围压的增加有助于改善水合物沉积物的受压变形能力；
3) 水合物沉积物的内摩擦角随饱和度增加变化显著，而黏聚力变化幅度较小，水合物对沉积物力学特性的贡献主要是摩擦特性。
基金项目
国家重点研发计划(2017YFC0307604)与中央高校基本科研业务费专项(16CX05001A)资助项目。
NOTES
*通讯作者。