基于四种季节属性HWT模型的电力需求预测

Electricity Demand Forecasting Using HWT Model with Four-Fold Seasonality

摘要: 基于日、周和年三种时间属性的滑动平均模型预测方法已经在电力需求短期预测方面得到了广泛应用。在本文中，我们研究了一种新的短期电力需求的模型和预测方法，即在日、周和年时间属性的基础上增加了一个月周期，并将这种新的周期应用到HWT模型中得到基于四种时间周期属性的预测算法，通过新加坡市场电力需求预测模型仿真得知，新的包含月周期的预测方法准确性更高。

Abstract: Seasonality methods have been developed to model the intraday, intraweek and intrayear seasonal cycles of the electricity load data in one-day ahead electricity demand forecasting. In this paper, we investigate the short-term modeling and forecasting of electricity demand where an intramonth cycle has also been discovered. Thus based on the intramonth cycle, a new mathematical modeling scheme is developed for HWT exponential smoothing model to accommodate the intramonth seasonal cycle and by using six years of Singapore data. We show that fourfold seasonal method outperforms the triple seasonal method in Singapore.

1. 引言

在电力工业系统中，电是通过电厂产生，然后通过电网输送和分配给负载终端 [1] 。由于电力不能有效地储存，电力系统的稳定性要求电力产生和消耗之间始终保持功率平衡。因此，准确的提前需求预测对生产者和消费者都十分重要。通过准确的电力需求预测，发电厂可以更有效地安排发电量以减少损耗；电力消耗终端也可以从实时调度中获益，社会效益将得到最大化 [2] 。此外，准确的电力需求预测也将有助于系统安全评估、网格自动控制和维护 [3] [4] 。需求预测方法可分为基于参数的方法和基于人工智能的方法。前者将模型描述为一组数学函数，其中参数的选择直接影响数学模型的准确性，而基于人工智能的方法利用如神经网络等模型中的非线性函数逼近和预测能力。近年来，在电力需求建模和预测方面取得了广泛的成果：如基于参数的模型 [5] [6] [7] ，基于人工智能的模型 [8] [9] [10] [11] 等。Holt Winters Taylor (HWT)指数平滑模型 [5] [6] 和自回归滑动平均模型(ARMA) [5] [7] 是两种有效的基于参数的方法，其主要优点在于处理具有规律的时间序列的预测上能发挥优良性能。另一方面，人工神经网络(ANN) [8] [9] ，径向基函数网络(RBFN) [10] [11] 和专家系统 [12] [13] 等基于人工智能的方法也得到了广泛的使用。此外，卡尔曼滤波 [14] 和小波变换技术 [15] 也被广泛应用于这一领域。以上列举的各种方法都有自己的特点，如模糊逻辑专家系统依赖于专家经验提取的大量规则，因此操作者的经验不一致和不可靠。对于上述所有方法，基于三种时间属性的HWT指数平滑模型在短期电力负荷预测方面都优于所有其他需求预测模型 [5] 。一般说来，对于城市级电力需求预测这种波动较小规律性较强的时间序列预测问题，基于参数的预测方法的预测精度更高。因此HWT预测算法和ARMA预测模型等方法也得到更多的关注。目前可见的基于参数的预测方法都采用了日、周和年这三个周期时间属性。

我们发现，月周期也能够被利用在电力需求的时间序列预测中，因为电力需求的波动有一定的月周期属性，这主要是由能源市场的独特性所决定。通常大的电力消费者如冶炼厂等会与发电厂以月为单位签订Take-or-Pay (TOP)协议，根据该协议，在一个月内不管消费者能否用完月额度，消费者都需要付整个月额度的钱，从而避免浪费，所以在月底的时候冶炼厂等消费者会加班加点生产下一月度的计划，用完整个月的电力消费额度。所以在月底的时候电力消费要明显高于月初的时候，这就说明了电力需求波动会有一定的月周期属性。在电力预测方面，需要我们去利用这一周期属性。虽然道理很简单，但是已有的文献中都没有从这个方面进行考虑。

本文提出了一种基于四种时间周期属性的电力需求预测自适应Holt Winters Taylor指数平滑算法，四种时间周期属性包括日、周、月、年四种。通过新加坡电力需求历史数据的仿真得知，我们本文提出的预测算法能够更加精确的预测未来短期电力需求，可以证明基于四种时间周期属性的方法要优于前面文献中提到的方法。本文所提出的指数平滑方法可以在其它的预测领域得到应用，比如企业准确的现金流预测 [16] 等。本文主要的贡献在于通过额外的一个月周期属性建立了新的多周期属性的预测数学模型。

2. 标准三季度HWT指数平滑模型

HWT 指数平滑模型由Brown, R.G.和Holt, C.C.首先提出，用于描述季节性时间序列的趋势 [17] [18] ，然后由J.W. Taylor进一步扩展到双季节性模式 [6] 。该模型良好的鲁棒性和预测的高精度使得其在季节时间预测方面得到了广泛的应用。由于有白天和夜晚、工作日和周末、夏天和冬天的区别，日模式、周模式和年模式的电力需求各有不同，周期属性在HWT指数平滑模型中通常被当做一个时间属性的模式参考。标准三种时间属性的HWT指数平滑模型可以描述为

$L\left(t\right)=\alpha \left[d\left(t\right)-\left(T\left(t-1\right)+S_1\left(t-s_1\right)+S_2\left(t-s_2\right)+S_3\left(t-s_3\right)\right)\right]+\left(1-\alpha \right)\left(L\left(t-1\right)+T\left(t-1\right)\right)$

$T\left(t\right)=\beta \left[L\left(t\right)-\left(L\left(t-1\right)+T\left(t-1\right)\right)\right]+\left(1-\beta \right)T\left(t-1\right)$

$S_1\left(t\right)=\gamma \left[d\left(t\right)-\left(L\left(t-1\right)+T\left(t-1\right)+S_2\left(t-s_2\right)+S_3\left(t-s_3\right)\right)\right]+\left(1-\gamma \right)S_1\left(t-s_1\right)$

$S_2\left(t\right)=\lambda \left[d\left(t\right)-\left(L\left(t-1\right)+T\left(t-1\right)+S_1\left(t-s_1\right)+S_3\left(t-s_3\right)\right)\right]+\left(1-\lambda \right)S_2\left(t-s_2\right)$

$S_3\left(t\right)=\delta \left[d\left(t\right)-\left(L\left(t-1\right)+T\left(t-1\right)+S_1\left(t-s_1\right)+S_2\left(t-s_2\right)\right)\right]+\left(1-\delta \right)S_3\left(t-s_3\right)$

$\hat{d}\left(t,k\right)=L\left(t\right)+kT\left(t\right)+S_1\left(t-s_1+k\right)+S_2\left(t-s_2+k\right)+S_3\left(t-s_3+k\right)$

其中，L是平均级电力需求，T是电力需求趋势，S₁、S₂、S₃分别是日模式、周模式和年模式的时间属性项，s₁、s₂和s₃的定义类似于原始模型，α、β、γ、λ和δ是相应的平滑参数。d(t)是在时刻t的真实电力需求， $\hat{d}\left(t,k\right)$ 是在时刻t的第k步提前预测。同时，忽略所有每年模式的相关项，则可得到双季节HWT指数平滑模型。

平均级电力需求L，需求趋势T 和时间属性项S₁、S₂、S₃，都是由历史电力需求数据估计而来，同时根据过去四年采集的数据来利用标准基因算法(GA) [19] [20] 估算最优平滑参数α、β、γ、λ和δ。本文中，我们利用提出的改进GA算法来确定最优或者次优参数集α、β、γ、λ和δ。GA算法是由Holland提出的一种随机搜寻方法，这种方法可以模仿基于达尔文的“适者生存”原则的生物系统的发展过程，并相对于其他仿生优化算法，该算法是应用最广泛的算法之一。GA算法是一种基于群体的自适应搜索技术，当搜索空间足够大时，它是极其有效的。

3. 四种季节HWT指数平滑模型

新加坡国家能源市场中，每月花费超过500新币的非家用消费者可选择成为电力自由消费者，他们可以和任意电力零售商以协议价格签署电力供应合同。通常情况下，消费者和零售商签订的合同是Take-or-pay (TOP)合同，这种合同是一种买卖双方签订的书面协议，要求无论买方是否用完了一个月的配额，买方依旧按月满配额结算，按时付款。因此为了减少浪费，消费者将在每个月底消费使用更多的电。图1显示了平均每日耗电量，具有以下特性：

1) 每月底的电力消费量大于每月前十天的电力消费量；

2) 每月的最后一天的电力消费量最低。

Figure 1. The average daily electricity consumption in Singapore

图1. 新加坡平均每日耗电量

$L\left(t\right)=\alpha \left[d\left(t\right)-\left(T\left(t-1\right)+S_1\left(t-s_1\right)+S_2\left(t-s_2\right)+S_3\left(t-s_3\right)+S_4\left(t-s_4\right)\right)\right]+\left(1-\alpha \right)\left(L\left(t-1\right)+T\left(t-1\right)\right)$

$T\left(t\right)=\beta \left[L\left(t\right)-\left(L\left(t-1\right)+T\left(t-1\right)\right)\right]+\left(1-\beta \right)T\left(t-1\right)$ ，

$S_1\left(t\right)=\gamma \left[d\left(t\right)-\left(L\left(t-1\right)+T\left(t-1\right)+S_2\left(t-s_2\right)+S_3\left(t-s_3\right)+S_4\left(t-s_4\right)\right)\right]+\left(1-\gamma \right)S_1\left(t-s_1\right)$ ，

$S_2\left(t\right)=\lambda \left[d\left(t\right)-\left(L\left(t-1\right)+T\left(t-1\right)+S_1\left(t-s_1\right)+S_3\left(t-s_3\right)+S_4\left(t-s_4\right)\right)\right]+\left(1-\lambda \right)S_2\left(t-s_2\right)$ ，

$S_3\left(t\right)=\delta \left[d\left(t\right)-\left(L\left(t-1\right)+T\left(t-1\right)+S_1\left(t-s_1\right)+S_2\left(t-s_2\right)+S_4\left(t-s_4\right)\right)\right]+\left(1-\delta \right)S_3\left(t-s_3\right)$ ，

$S_4\left(t\right)=\zeta \left[d\left(t\right)-\left(L\left(t-1\right)+T\left(t-1\right)+S_1\left(t-s_1\right)+S_2\left(t-s_2\right)+S_3\left(t-s_3\right)\right)\right]+\left(1-\zeta \right)S_4\left(t-s_4\right)$ ，

$\hat{d}\left(t,k\right)=L\left(t\right)+kT\left(t\right)+S_1\left(t-s_1+k\right)+S_2\left(t-s_2+k\right)+S_3\left(t-s_3+k\right)+S_4\left(t-s_4+k\right)$

模型(1)代表一种新的HWT指数平滑方法，该方法可以用于获取日、周、月、年四种时间周期属性。这种四个时间周期属性的方法是在基于三种时间属性方法的表达式基础上进一步包含了第四个时间属性和额外的平滑公式。在这个公式中，lt、dt、S₁和S₂与三种时间属性模型意义相同。S₃和S₄定义为月和年这两种时间周期属性。

Figure 2. Average intraday cycle for each day of the week

图2. 一周内的平均日内周期

4. 应用四种时间周期属性方法进行电力预测

4.1. 数据：新加坡的历史电力需求

本章节将利用从2009年到2013年这五年内每半小时的新加坡真实的电力需求数据来验证所提出的四种时间属性方法的有效性。前两年的数据用于估计预测方法的参数，剩下三年的数据用于验证后验预测的准确性。图2用于表示一周内的平均日内周期，由此可见一周内的每一天日内周期都不相同。总的来说，周日是一周内电力需求最低的一天，而傍晚则是每天中电力需求最高的时刻。周六和周日类此，只是早上有一个高峰时刻出现。历史电力需求的具体要求和放大的图片可以分别如图3和图4所示，其中，可以看到存在着强烈的每天、每周和每年的季节属性。

如图4所示，相比较于平时，公共假期(上周的第三天)可以看到异常的电力需求出现，这种现象会给电力需求模型的简历制造障碍。为了消除这些异常值得影响，一般可以用上一周同一时间的数据来代替公共假期的电力需求数据，这样可以近似接近原始模型。然而，一个更有效的方法是利用本文提出的方法，用基于标准模型如ARMA模型和神经网络模型等的预测值需求来代替公共假期的电力需求数据。这种方法被证明比原始模型方法更有效 [7] [8] 。在下面的仿真验证中可以看到当使用新放来代替公共假期的电力需求数据可以明显降低整个模型的预测误差。

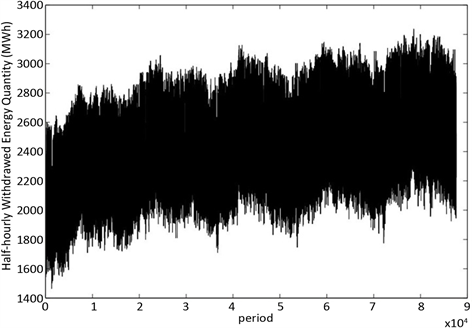
Figure 3. Electricity demand time series of Singapore (Jan 2009-Sep 2014)

图3. 新加坡电力需求的时间序列(2009年1月~2014年9月)

4.2. 模型评价指标

为了评估三种季节属性的ARMA，HWT和IC指数平滑模型的电力需求预测的准确性，我们在每个模型中都将用从00:00开始的半小时超前时间来预测未来24小时的电力需求，并利用绝对百分比误差absolute percentage error (APE)进行比较。绝对百分比误差可以定义为

$AP{E}_i=\frac{1}{n}{\displaystyle {\sum }_{j=1}^N\left|\frac{d_{ij}-\widehat{d_{ij}}}{d_{ij}}\right|},i=1,\cdots ,48,j=1,\cdots ,N$ (1)

其中，d_ij是第j天的第i个半小时的真实电力需求， $$ 是相应的预测需求。在电力系统中，大规模的经济损失可能会导致在特定时间段的预测需求误差较大。因此，另一种模型预测标准，最大绝对百分比误差maximal absolute percentage error (MAPE)，定义为

Figure 4. Half-hourly electricity demand time series of Singapore (Jan 2009- Sep 2014)

图4. 半小时电力需求时间序列(2009年1月~2014年9月)

$MAP{E}_i=\frac{1}{10}{\displaystyle {\sum }_{m=1}^{10}\left|\frac{d_{im}-\widehat{d_{im}}}{d_{im}}\right|},i=1,\cdots ,48,m=1,\cdots ,10$ (2)

其中，m为第i半小时的最大需求误差为前十的天数。

4.3. 仿真结果

四种时间属性HWT指数平滑模型的参数可取为α = 0.01，β = 0.25，γ = 0.04，λ = 0.1，δ = 0.032，ζ = 0.01，这些参数的选择是根据GA算法，通常来说，四种时间属性的HWT指数平滑模型的性能是要比三种季节属性的方法要好，这是因为它包含了更多的时间属性。由图5中的红线可知，四种时间属性HWT指数平滑模型具有1.61%的平均APE，两种季节属性方法只有1.67%平均APE。尽管在预测APE时这两种方法性能相近，三种季节属性的方法在预测MAPE上要具有更优的性能。图6显示的是前十大预测误差的平均值。

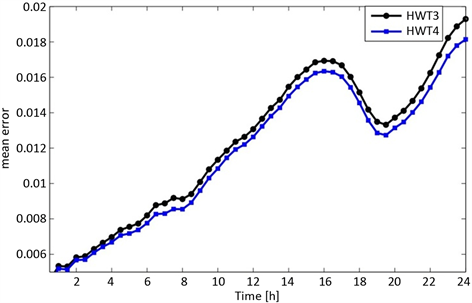
Figure 5. Forecasting APE in HWT exponential smoothing model

图5. 四种时间属性HWT指数平滑模型

Figure 6. Forecasting MAPE in HWT Seasonal model

图6. HWT季节模型中预测的MAPE平均值

5. 结论

本文对新加坡电力市场的电力需求进行了预测，首先研究了标准电力需求模型，即HWT指数平滑模型。该模型在热带区域例如新加坡的电力预测可以取得良好的预测精度。为了进一步提高预测精度，本文提出了四种时间属性的模型并在仿真中证明该模型在提升预测精度方面的有效性。