1. 引言
ESMD [1] [2] 是英文“Extreme-point Symmetric Mode Decomposition”的简称,其中文意思是“极点对称模态分解”。该方法是希尔伯特-黄变换方法 [3] [4] [5] 的新发展,由两部分组成:第一部分是模态分解,可以产生数个模态与一条最佳的自适应全局均线;第二部分是时-频分析 [6] 。本文主要针对ESMD方法的第一部分进行改进,原方法具体计算步骤如下:
该方法只考虑一维观测数据,即通常所谓的“时间序列”,记为
,其中N是一个正整数。先是找出数据Y的所有极值点(极大值和极小值点),对相邻极值点用线段连接并将线段中点依次记为
,然后通过一定方式补充左、右边界中点
、
,利用所获取的
个中点构造p条插值线
并计算它们的均值曲线
,然后对
重复上述步骤直到
,(
是预先设定的容许误差)或筛选次数达到了预先设定的最大值K。此时分解出第一个经验模
,再对
重复上述操作依次获得
直到最后余量R只剩一定数量的极值点。
最后的剩余模态R为“自适应全局均线(adaptive global mean curve)”,简称AGM曲线。事实上,只有当数据的拟合曲线是最佳的,去掉该曲线的剩余信号才可以被视为脉动量,进而可分解出一系列波动信号并认识其时-频变化特征。记原始信号为
,则其全局平均(数学期望)为
(1)
相应的方差为
. (2)
这种常值形式的平均是最简单的全局均线形式。其实作为全局均线应当能够反应数据的总体变化趋势。这里的AGM曲线
是由数据自动优选出来的,具有数据自适应特点。这里优选借用了“最小二乘”策略,此时的方差定义为
(3)
在实际应用中,我们通常选取
,采用标准差比率
(4)
来反应AGM曲线R相对于全局平均
的优化程度。
在数据分析中对称性与周期性关系密切,ESMD方法采用的是极点对称法则,这与我们以往所知道的周期的概念并不一样。一个极大值点与相邻的两个极小值点之间为一个周期,或者一个极小值点与相邻两个极大值点之间构成一个周期,也就是说两个相邻极值点之间是半个周期。极点对称反映的是连接极大值点和相邻极小值点的线段中点,所有对称中点都位于零值线上,这个中点称为局部中点。
ESMD方法适用于非线性、非平稳信号,如气候 [7] 、海气通量 [8] 等随机的时间序列数据,其在处理对称数据时取局部中点具有很好的代表性,分解之后的模态与自适应全局均线能准确的表达对称数据的信息与变化趋势。本文主要针对ESMD方法在处理非对称数据时所存在的缺陷对该方法进行改进。
2. ESMD方法在处理非对称数据时出现的问题及原因
基本上,符合时间序列的数据都可以用ESMD方法来处理,而且数据量越大效果越好。ESMD方法一般适应于在每半个周期中关于中点较对称(即极点对称)的数据。对于非对称数据(这时数据在形式上表现为峰谷不对称)来说,ESMD方法中选取的中点失去了代表性。峰谷不对称按照数学期望 [9] 来说,大部分数据点位于局部中点的一侧,只有一小部分位于另一侧,从而造成数据线峰谷不对称的现象。
本文针对非对称数据的一般示例进行讨论,即某一条河流近几十年的地表径流量数据。地表径流量的数据之所以不对称是因为春秋冬三季降雨量少,而夏季雨水较多。数据虽然具有较强的周期性,但是在每半个周期上并不关于局部中点对称,大部分都集中在局部中点的下方。这时如果用ESMD方法对数据进行处理,取中点并不能客观的代表原数据的趋势,反而会产生较大的偏差。所以最后求得的AGM曲线与原数据的标准差
比全局平均与原数据的标准差
要大,在筛选次数从1到40时,代入(4)式得到的标准差比率v都是大于100%的(如图1)。这种情况说明,数据的非对称性使得自适应全局均线反而比不上整体的平均值 [2] 。可以看出ESMD方法在处理类似于地表径流量这类非对称数据时存在极大的误差,从而严重影响最后结果的可信度。
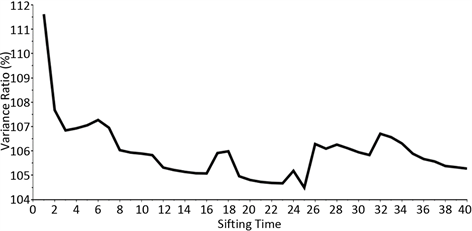
Figure 1. Standard deviation ratio with different screening times (original method)
图1. 筛选次数不同时的标准差比率(原方法)
3. ESMD改进算法的实验结果与分析
本文针对上述这种特殊情况,对ESMD方法进行改进,将这时不具有代表性的中点替换为能反应每半个周期数据情况的局部均值。每半个周期内的数据全部相加后除以相应的个数,即为局部均值。这时得到的自适应全局均线设为
,设求得与原数据
的方差为
(5)
标准差比率为
. (6)
图1是原ESMD方法取局部中点时,求得筛选次数不同所对应不同的标准差比率。从图中可以看出最佳筛选次数为25次,对应的最小标准差比率为
。
图2是改进的ESMD方法取局部均值时,求得筛选次数不同所对应不同的标准差比率。从图中可以看出最佳筛选次数为23次,对应的最小标准差比率为
,并且最大的方差比率也没有超过101.5%。
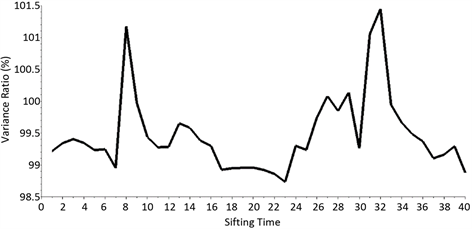
Figure 2. Standard deviation ratio with different screening times (improved method)
图2. 筛选次数不同时的标准差比率(改进的方法)
从1到40次筛选次数对应的方差比率可以看出,改进的ESMD方法明显比原方法的结果有了明显的优化,不仅方差比率降低了,筛选次数也相应减少了,从而节省了计算时间。
图3(a)表示原方法的模态分解,(b)表示原方法的数据与全局自适应均线的对比图,图4(a)表示改进方法的模态分解,(b)表示改进方法的数据与全局自适应均线的对比图。从图3(a)与图4(a)可以看出两种方法下的模态分解虽然有差距,但并不是很大。从图3(b)与图4(b)可以看出两种方法得到的全局自适应均线虽然形态近似,但是范围不同,原方法得到的全局自适应均线变化较剧烈,在极小值点几乎不变的情况下,受到极大值点的影响很明显,变化的范围在
到
之间;而改进的方法得到的自适应全局均线受极值点的影响较小,变化范围在
到
之间。
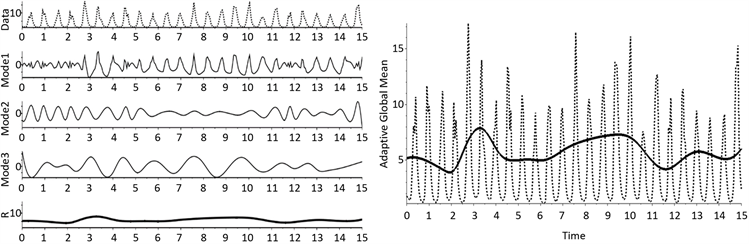 (a) (b)
(a) (b)
Figure 3. Modal decomposition and adaptive global mean (original method)
图3. 模态分解和自适应全局均线(原方法)
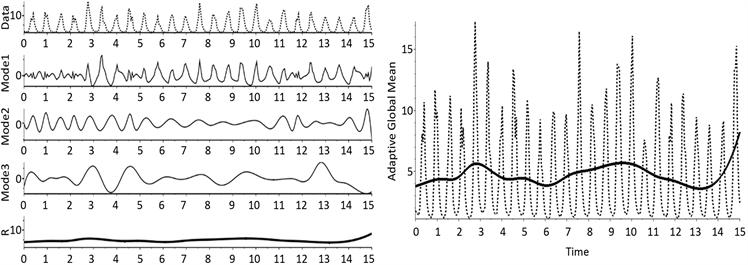 (a) (b)
(a) (b)
Figure 4. Modal decomposition and adaptive global averaging (improved method)
图4. 模态分解和自适应全局均线(改进的方法)
图5为原方法与改进方法得到的自适应全局均线的比较图放大后的部分图像,从图中可以看出改进方法后得到的AGM曲线明显比原方法的AGM曲线整体下移,且变化更加平缓。
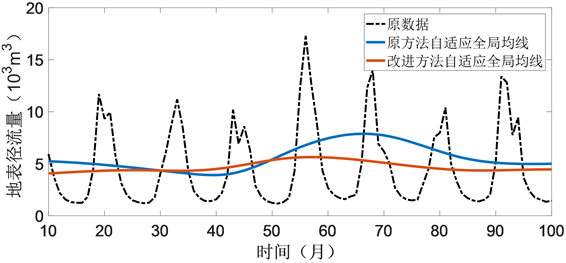
Figure 5. Comparison between the original method and the improved method adaptive global moving average
图5. 原方法与改进方法自适应全局均线的比较
针对ESMD方法优化前与优化后,基于“最小二乘法”进行方差验证,比较结果如表1。全局平均与原数据的方差为13.32,局部中点插值后的数据与对应原数据的方差为12.50,局部均值插值后的数据与对应原数据的方差为8.06。

Table 1. System resulting data of standard experiment
表1. 标准试验系统结果数据
从表1中可以看出,在非对称数据基础上,局部均值插值后的数据与原数据的方差小很多,从而证明局部均值比局部中点更具有代表性。
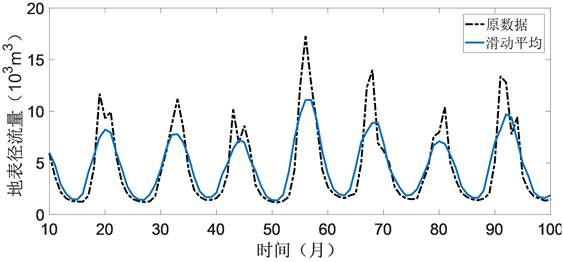
Figure 6. 5 points sliding average processing was performed on the original data
图6. 对原数据进行五点滑动平均处理
图6是对原数据进行五点滑动平均处理后的一部分图像,从图中可以看出五点滑动平均与原数据拟合较好,细节未丢失,但是并没有反映出数据的总体趋势,相比之下,ESMD方法既有数据不同模态下的变化趋势,并且最后得到的是自适应全局均线,反应数据的总体趋势,事实证明ESMD方法对数据分析方面非常全面。
4. 结论
本文提出的用局部均值代替局部中点对非对称数据进行ESMD方法的模态分解,编入程序后得到的结果明显优于之前的算法。最后筛选出的自适应全局均线更能准确的反应数据的总体变化趋势与数值变化范围。由此可看出,对于非对称数据处理,局部均值比局部中点更具有代表性。