1. 引言
在本文中,我们研究Boiti-Leon-Pempinelle (BLP)系统
(1.1)
的行波解。Boiti等人 [1] 首先建立了BLP系统的可积性。之后,文献 [2] - [13] 给出了许多不同的行波解。但因为没有考虑到BLP系统所对应的行波系统的所有分支相图,这些文献所求出来的行波解并不完整。本文也将基于行波变换
(1.2)
来研究系统(1.1)的其他行波解,其中c表示波速。将变换(1.2)代入系统(1.1),得到
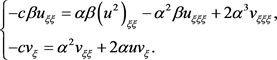 (1.3)
(1.3)
对系统(1.3)的第一个等式对
进行两次的积分,得
(1.4)
令
,则(1.4)可简化为
(1.5)
从(1.3)第二个等式可以得到
(1.6)
因此,我们对方程(1.5)进行求导,可得
(1.7)
再将等式(1.5)和(1.7)代入(1.6),得到
(1.8)
利用
,则系统(1.8)改写成如下形式
(1.9)
它的首次积分为
(1.10)
其中h是积分常数。
本文的主要目的就是通过动力系统的分支理论 [14] [15] [16] [17] 来研究系统(1.1)的行波解。我们的贡献包括如下三点:
1) 本文在函数
之上建立了系统(1.1)一个新的哈密顿函数。
2) 基于定性理论和哈密顿函数,我们证明了该系统异宿轨的一个有趣现象,即异宿轨的存在与积分常数g无关。
3) 应用动力系统的分支理论,我们得到了系统(1.1)的平滑和非平滑行波解的精确表达式。
2. 主要结论
在本节,我们列出了BLP方程的平滑和非平滑行波解。为方便起见,先定义如下
定理2.1:当
时,系统(1.1)的精确行波解如下:
1) 三个周期波解
(2.1)
(2.2)
(2.3)
2) 三个扭结波解
(2.4)
(2.5)
(2.6)
3. 理论推导
现在,我们先讨论由首次积分(1.10)所确定的水平曲线的动态。令
(3.1)
有三个零点
(如图1),由下式给出
(3.2)
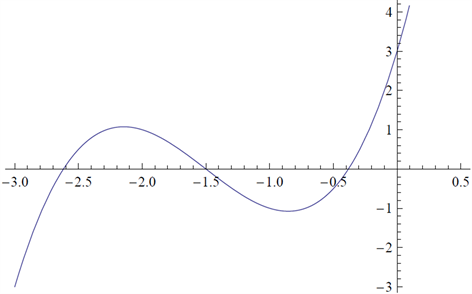
Figure 1. The figure of
for
and
图1.
在
且
时的图像
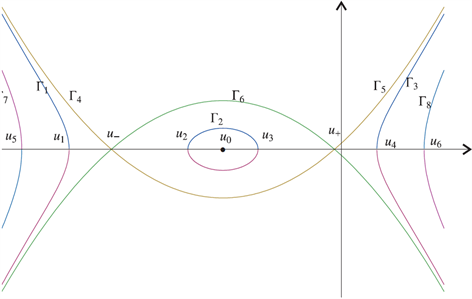
Figure 2. The phase portrait of the BLP equation
图2. BLP方程的相图
由(1.1)的相图(如图2),可以看出,存在通过点
的轨道
。它的轨道的显式表达式为
(3.3)
其中,
,
,
,且
。
再将(3.3)代入
,并沿着
进行积分,我们得到
(3.4)
通过查找积分表得到行波解(2.1)。
同理,我们可以继续沿着轨道
进行积分,并得到相应的行波解(2.2)~(2.6)。
4. 结论
本文我们通过动力系统的分支理论证明了行波的存在并证明了扭结波的存在性不受波速和积分常数的影响。同时我们发现一个新的不同于参考文献 [2] 中的哈密顿函数,并得到新的行波解。
从这个意义上讲,我们丰富了Boiti-Leon-Pempinelle方程的性质,并证明了所涉及方法的适用性。