1. 引言
雷击对于电网安全运行的影响一直备受关注,统计表明,包括山东电网在内,220 kV及以上交流输电线路,由于雷击引起的跳闸和重启的概率超过半数 [1] 。目前输电线路的设计中,防雷主要采用规程法和电气几何模型法(electro-geometric model, EGM) [2] ,国内外也提出了改进的EGM和先导模型法(leader progression model, LPM)等 [3] 。规程法主要基于早期30 m以下单回路矮塔设计的经验总结而来,有很大的局限性,在如今高杆塔的防雷设计研究中并不适用。先导模型法由于雷电现象的复杂多样性,诸多学者对雷击物理过程的描述还有很大分歧,且对雷电和长间隙试验观测的数据过于依赖。EGM是把雷电的放电特性和杆塔结构尺寸等因素结合起来进行分析,与实际运行经验相符合,具有很好的普适性。本文在山东地区差异化防雷研究中,使用EGM法。
山东地理位置处于我国东部沿海地区,属于我国雷暴频发地区,且地形地貌复杂多样,不同地区雷暴日差别明显 [4] [5] ,各地不同的气候特征,对于雷电活动也有明显影响 [6] [7] 。本文以山东电网为例,基于改进的电气几何模型法,研究了架空线路的差异化防雷,对提高输电线路运维水平,减少雷电活动对电网的破坏,具有至关重要的作用。
2. 地区不同雷电活动影响
山东省是我国受亚洲夏季风影响最强的地方之一,山东中部地区年平均雷暴日大于25 d,由于地形、纬度等因素的影响,鲁中山区和鲁南沂蒙山区雷暴日数较多,其中沂源的雷暴日达到36 d,而威海的石岛雷暴日较少,只有16 d [8] 。各个地区雷暴日差别较大,雷电分布的差异决定了在防雷计算与设计中不能简单地使用单一固定的雷电参数。
目前工程上使用的雷电定位系统都是比较先进的,理论上可以实时完整的记录覆盖区域内的地闪发生情况。因此使用合适的方法便可以较为准确地统计出线路走廊内实际的地闪发生情况。但是有些地区地闪密度分布数据并不完备,尤其是新建线路的数据更少。此时可根据地区的雷暴日来近似计算地闪密度从而实现差异化防雷设计。
IEEE 1243-1997推荐地闪密度可以利用公式(1)来计算。
(1)
式中:
为雷暴日。
计算输电线路雷击跳闸率的时候,每100km线路每年遭受雷击次数,通常用公式(2)计算。
(2)
式中:
为地闪密度;b为两根避雷线间距离;
为避雷线平均高度;
为线路电压等级。
现行规程法所使用的雷电流幅值分布函数的计算方法以及相应的雷电流幅值密度函数的计算方法如式(3)所示。
(3)
式中:C为常数,在我国一般地区C通常取88,在某些特殊地区如西北地区(不包括陕南)和内蒙古自治区部分地区C通常取44。
IEEE推荐的雷电流幅值分布函数的计算方法以及相应的雷电流幅值密度函数的计算方法如式(4)所示。
(4)
利用规程法和IEEE推荐公式分别计算雷电流密度并对比实测值发现,IEEE公式更接近山东实际雷电流分布情况,如表1所示,因此,雷击跳闸率计算中,山东地区的雷电流幅值分布及其概率的计算推荐采用IEEE推荐的公式。

Table 1. The discipline method is compared with the IEEE recommended formula
表1. 规程法与IEEE推荐公式比较
3. 反击跳闸率影响因素及其计算
雷电直击于线路架空地线或者杆塔时,雷电流一部分经架空地线流向线路两侧,大部分经杆塔及接地装置流入大地,引起塔顶电位升高,而造成绝缘子串的闪络放电,这种现象称为反击。雷电反击过电压与雷电参数,杆塔型式、高度和接地电阻等。
3.1. 反击跳闸率的计算
线路绝缘按照塔头绝缘,即绝缘子串或塔头间隙的50%冲击放电电压计算,则雷击杆塔时的反击跳闸率按照公式(5)计算。
(5)
式中:N为年雷击次数;
为绕击率;g为击杆率;
为建弧率;
为雷击杆塔超过耐雷水平
的概率,
按照上述公式(4)计算。
击杆率是指雷击杆塔的次数与线路遭受雷击的总次数的比值,击杆率的大小受地线根数和地形因素的影响。按照表2计算。

Table 2. Different terrain Striking Rate
表2. 不同地形击杆率表
3.2. 线路耐雷水平的计算
雷击塔顶反击的耐雷水平,按照公式(6)计算。
(6)
式中:
表示绝缘子串正极性50%冲击放电电压;
为杆塔高度,m;
表示横担对地高度,单位m;
表示杆塔分流系数;
表示导线平均高度,单位m;k表示导线和避雷线间的耦合系数;
表示导线和避雷线间的几何耦合系数;
表示避雷线对地平均高度,单位m;
表示杆塔冲击接地电阻,Ω;
为雷电波形的波头时间,μs;
为杆塔等值电感。
输电线路杆塔的分流系数是指由于避雷线具有分流的作用,使雷电流只有一部分流过杆塔电感和接地电阻。分流系数可以按照表3来进行选择。
建弧率可用公式(7)计算。
(7)
式中:E为工频弧道平均电场强度。
当中性点有效接地,可用公式(8)计算,中性点非有效接地时,可用公式(9)计算。
(8)
(9)
式中:
为系统额定电压,V;
为绝缘子闪络距离,m;
为木横担间距,若为铁或水泥横担,则为0,m。
雷击塔顶时,地线上的冲击电压超过地线的起始电晕电压,地线上将出现电晕。由于电晕的存在,地线的径向尺寸影响范围将会增大,需要考虑电晕的影响,此时导线的几何耦合系数应当乘以电晕校正系数。
对于22~500 kV等特高压以下输电线路路,一般需要考虑冲击电晕对线路的影响,表4为通常情况下简单修正电晕影响时所需要的校正系数。

Table 4. Corona correction factor for lightning strikes the top of the tower
表4. 雷击塔顶时的电晕校正系数
3.3. 电磁环境对防雷设计的影响
在特高压交直流输电线路的防雷设计中,还必须考虑电磁环境情况这一重大技术问题。因此,对于线路耦合系数来说,分为特高压以下线路耦合系数计算和特高压考虑冲击电晕的耦合系数计算两种方式。
当不考虑冲击电晕的影响时,输电线路各相导线自波阻抗与互波阻抗用公式(10)和公式(11)表示。
(10)
(11)
式中:
表示各相导线与其他导线镜像之间的距离,单位m;
表示各相导线对地高度,单位m;
表示各项导线之间的距离,单位m;
表示导线半径,单位m。
当考虑冲击电晕的影响后,此时输电线路导线的等值波阻抗计算如公式(12)所示。
(12)
式中:
表示几何波阻抗,单位Ω;u表示导线上的工作电压,单位V;
表示线路上的起晕电压,单位V;M为常数,正极性时,M = 1.36,负极性时,M = 1.13。
分裂导线电晕起始电压的值按照公式(13)所示。
(13)
式中:r表示导线半径,单位m;n表示分裂导线数;
为起晕场强,单位V/m;
为分裂导线等效半径,m;A表示分裂间距,单位m;起晕场强的计算由Peek公式得到,即公式(14)所示。
(14)
式中:m为导线表面粗糙系数;
表示相对空气密度系数。
分裂导线间距可用公式(14)表示
(15)
式中:d为相邻两根分裂导线的距离,m。
计算线路分裂导线的等效半径如公式(16)所示。
(16)
线路双避雷线的起晕电压可用公式(17)计算。
(17)
式中:
为避雷线的半径,单位m;
表示避雷线的平均高度,单位m;D为避雷线间的距离,单位m。
求输电线路的自波阻抗,将其代入公式(18),即可得到电晕时的线间耦合系数。
(18)
式中:
表示线路的波阻抗矩阵[Z]中第m行第m列的代数余子式。
在输电线路计算中(特别是防雷计算)通常情况下不考虑杆塔上的波过程,而是用集中电感来模拟杆塔。我国规程给出了不同结构杆塔单位长度的电感值。该模型较简单、方便,并且可以根据数学公式直接计算求得线路反击耐雷水平,我国规程的防雷计算就采用此模型。但此方法是一简化计算方法,与实际生活中的雷击过程有一定的差距,因为将杆塔看作一等值电感,此时杆塔上任意点电位是相同的,这种情况下不能反映雷击杆塔顶部时雷电流在杆塔上的传播过程及反射波对杆塔各节点电位的影响与绝缘子串上电压随时间变化的过程。
随着电力系统的不断发展,线路杆塔的高度也在不断增加,早期根据30m以下架空线路杆塔设计的实践经验总结出来的电感模型有很大的局限性,对高塔的计算有较大误差,在如今高杆塔的防雷设计研究中并不适用。雷击塔顶导致的雷电流从塔顶流入大地的过程是一个暂态波过程,单波阻抗模型在这一方面与集中电感模型相比有了质的飞跃。这两种模型分别反映了2种完全不同的物理过程,而波阻抗模型更接近于实际情况,并且这两种模型塔顶过电压的表示方式是不一样的。经塔底反射回的过电压波和雷电产生的过电压波的同作用产生波阻抗模型中的塔顶过电压;而在电感模型中,线路杆塔的接地电阻和塔身的等效电感感抗上的电压降之和表示塔顶的过电压。对比现阶段的各种计算模型,其中日本的山本修、原武久2人给出的计算公式与工程实际更加接近,受到较多试验数据资料的支持。如公式(19)所示。
(19)
式中:c为光速;t为杆塔遭受雷击时计时时刻。
关于原武久给出的公式(19),计算得出的波阻抗随着时间的变化而变化,在高杆塔防雷设计中,可以只采用简单的静态波阻抗模型,即取波阻抗的最大值进行设计。如公式(20)所示。
(20)
若双回特高压塔架有导线与避雷线,常采用多层传输塔模型,目的是研究杆塔的雷电冲击响应特性,并且预测线路杆塔在遭受雷击时其绝缘子串反击闪络的情况。目前的杆塔模型很难将其结果推广到结构较为复杂的传输塔上,大多适用于结构简单的传输塔,因为这些模型很少有考虑横担与支架对杆塔Z产生的影响。因此在差异化防雷的设计中,建议采用西安交大提出的多波阻抗模型如公式(21)所示。该模型计算相对简单,并与Hara提出的无损杆塔模型一致性较高 [9] 。其多阻抗模型示意图如图1所示。

Figure 1. Multi-wave impedance model diagram
图1. 多波阻抗模型示意图
(21)
(22)
(23)
4. 绕击率影响因素及其差异化计算
由于先导模型法还不是很成熟,而EGM具有很好的可操作性,建议架空输电线路绕击雷电性能的计算采用EGM法。对于水平导体,针对雷击距这点来讲,不同学者研究所得出的雷击距公式是不同的,并且大多数学者没有考虑线路架设的高度差异对击距产生的影响,得出的公式只是雷电流的一元方程。Eriksson提出的雷击距公式具有更好的普适性 [10] 。雷电绕击的电气几何模型如图2所示。
Eriksson提出的计算方法如公式(24)所示。
(24)
式中:h为导线平均高,m;I为雷电流幅值,kA。
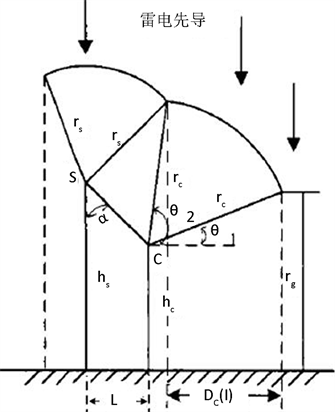
Figure 2. Schematic diagram of conventional lightning strike model
图2. 常规雷电绕击模型示意图
雷电先导的对地击距与对导线击距的比值(击距系数)是随着导线高度的增加而减小的,IEEE工作组提出当导线的平均高度小于40 m时,对地击距如公式(25)所示。
(25)
对于超特高压线路,线路杆塔,先导对大地的击距与其对避雷线和导线的击距是不相等的,因此当导线的平均高度大于40m时,对地击距如公式(26)所示。
(26)
雷击导线的区域随着雷电流的增加而减小,当雷电流达到某一程度时,击中避雷线或大地,线路不再发生绕击,此时称为最大绕击电流,其大小受到杆塔的尺寸、地形因素的影响。
计算最大绕击电流
。已知hs、hc、L求当
时的I值,即为最大绕击电流
。求出最大绕击电流
,即可进一步求出平原地形的绕击率。
的计算见公式(27)。
(27)
式中:
为避雷线和导线平均高度,单位m;L如图2,表示导线与避雷线间的的水平距离,单位m。
绕击闪络率及绕击跳闸率的计算见公式(28):
(28)
式中:
,其计算过程见式(2);
表示雷电流幅值分布,其计算见式(4)。
根据电气几何模型,绕击率计算还需要的公式,如公式(29)、(30)、(31)和(32)所示。
(29)
(30)
(31)
(32)
式中,
为避雷线平均保护角。
(33)
5. 结语
在日常生活中架空输电线路遭受雷击引起的线路跳闸事故,不但会使电力输送单位不能可靠供电,加大线路负担,增加线路以及设备的维护维修成本;而且当输电线路遭受直击雷时,产生的雷电波还会沿着线路传送到变电站中,可能进一步引发重大事故。本文针对雷电跳闸率的计算方法进行研究,结合山东地区地形地貌复杂、雷暴日差别明显以及气候因素,给出了更为符合山东地区防雷计算的改进电气几何模型法,对山东地区的差异化防雷作出贡献,对改进山东地区电网的输电线路设计防雷措施,增强输电线路供电的安全可靠性,保障发电厂、变电站的安全稳定运行具有重要的意义。
基金项目
本项目由山东电力工程咨询院有限公司科技项目资助(项目编号:37-2016-24-K0016)。