基于双密度双树复小波变换的图像压缩

Image Compression Based on Dual Density Dual Tree Complex Wavelet Transform

摘要: 随着多媒体信息技术的高速发展，产生了极其庞大的图像数据。当对这些数量庞大的图像数据进行存储和传送时，利用图像压缩编码技术减少其数据量是很有必要的。本文的研究目的是寻找一种压缩质量较好的图像压缩方法。本文在小波变换与图像压缩的理论基础上进行研究，提出了基于双密度双树复小波变换的图像压缩方法，通过Matlab仿真实验得出了实验结果的比较和分析，最终确认了该方法相比传统的图像压缩方法对图像的压缩质量有明显的优化。

Abstract: With the rapid development of multimedia information technology, the extremely large image data is produced. When these massive image data are stored and transmitted, it is necessary to use image compression coding technology to reduce the amount of data. The purpose of this study is to find a method of a better quality of compressed image. The paper is based on the theory of wavelet transform and image compression, and an image compression method based on dual-density du-al-tree complex wavelet transform is proposed. According to MATLAB simulation, experimental results are given. Finally, it is confirmed that this method has obvious optimization compared with the traditional image compression method for image compression quality.

1. 引言

近年来，信息技术和移动通讯的爆炸式发展，使得图像数据的传送有了海量的增长，伴随着高清和超清图像视频的普及，图像压缩编码技术发挥着越来越重要的作用。图像压缩 [1] 是在确保图像质量的基本要求下，实现尽可能大幅度地减小图像的数据量，当图像本身的数据大比例降低了，它的传输和存储就变得方便容易得多。

小波变换的图像压缩编码方法是先通过小波变换对图像进行多分辨率分解得到不同空间且不同频率的一系列子图像，再对所得的子图像分别进行系数编码。小波基函数的选择是其中关键的内容，选择不同的小波基函数来进行图像压缩所取得的压缩效果一般都不一样，本论文的研究中选择的是以双密度双树复小波变换作为小波基函数。

小波变换 [2] 在频域以及时域上有着良好的局部化特性，同时能够把图像数据信息定位至任意数量级的精度上。正是因为这些优点，基于小波变换的图像压缩编码方法逐渐发展并取代了传统的基于离散余弦变换和其他子带编码技术，成为当今应用广泛并且有着可观发展前景的数据压缩方法。

2. 双密度双树复小波变换

2.1. 双树复小波变换

一维双树复小波 [3] 以如下形式表示

$\psi \left(t\right)={\psi }_h\left(t\right)+j{\psi }_g\left(t\right)$ (2-1)

其中 ${\psi }_h\left(t\right)$ 表示复小波的实部， ${\psi }_g\left(t\right)$ 表示复小波的虚部，二者皆为实函数。双树复小波变换以此种方式用两个相对独立的实小波变换来表示。我们称双树复小波的实部为树A，称其虚部为树B。假定树A的低通滤波器为 $h_0\left(n\right)$ ，树A的高通滤波器为；树B的低通滤波器为 $g_0\left(n\right)$ ，树B的高通滤波器为 $g_1\left(n\right)$ 。在这里，与两组滤波器 $h_0\left(n\right)$ 及 $g_0\left(n\right)$ 相对应的小波基函数 ${\psi }_h\left(t\right)$ 及 ${\psi }_g\left(t\right)$ 近似满足Hilbert变换对，即：

${\psi }_h\left(t\right)\approx H\left\{{\psi }_g\left(t\right)\right\}$ (2-2)

二维双树复小波 [4] 可以通过对一维双树复小波作张量积的方法获得：

$\psi \left(x,y\right)=\psi \left(x\right)\psi \left(y\right)$ ，由(2-1)代入可得

$\begin{array}{c}\psi \left(x,y\right)=\left[\left({\psi }_h\left(x\right)+j{\psi }_g\left(x\right)\right)\right]\left[\left({\psi }_h\left(y\right)+j{\psi }_g\left(y\right)\right)\right]\\ ={\psi }_h\left(x\right){\psi }_h\left(y\right)-{\psi }_g\left(x\right){\psi }_g\left(y\right)+j\left[{\psi }_g\left(x\right){\psi }_h\left(y\right)+{\psi }_h\left(x\right){\psi }_g\left(y\right)\right]\end{array}$

2.2. 双密度小波变换

双密度小波变换 [5] 的分解是利用两个高通滤波器和一个低通滤波器来实现的。记尺度函数 $\phi \left(t\right)$ 及其相应的低通滤波器为 $h_0\left(n\right)$ ，小波函数 ${\psi }_1\left(t\right)$ 相应的高通滤波器为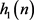，小波函数 ${\psi }_2\left(t\right)$ 相应的高通滤波器为 $h_2\left(n\right)$ ，则有

$\{\begin{array}{l}\phi \left(t\right)=\sqrt{2}{\displaystyle \underset{n}{\sum }{h}_0\left(n\right)\phi \left(2t-n\right)}\\ {\psi }_1\left(t\right)=\sqrt{2}{\displaystyle \underset{n}{\sum }{h}_1\left(n\right)\phi \left(2t-n\right)}\\ {\psi }_2\left(t\right)=\sqrt{2}{\displaystyle \underset{n}{\sum }{h}_2\left(n\right)\phi \left(2t-n\right)}\end{array}$ (2-3)

二维双密度小波变换可以通过对两个一维双密度小波变换进行行，列滤波获得。

2.3. 双密度双树复小波变换的获取

可以用两个双密度小波变换实现一维双密度双树复小波变换 [6] 。第一个双密度小波变换对应数A (实部)，第二个双密度小波变换对应数B (虚部)。树A使用一个低通滤波器 $h_0\left(n\right)$ 以及两个高通滤波器 $h_1\left(n\right)$ 和 $h_2\left(n\right)$ ，树B则是使用一个低通滤波器 $g_0\left(n\right)$ 及两个高通滤波器 $$ 和。记 $$ 和 $g_0\left(n\right)$ 对应的尺度函数分别为 ${\psi }_h\left(t\right)$ 和 ${\psi }_g\left(t\right)$ ， $h_1\left(n\right)$ 和 $h_2\left(n\right)$ 对应的小波函数为 $$ 和 ${\psi }_{h,2}\left(t\right)$ ， $g_1\left(n\right)$ 和 $g_2\left(n\right)$ 对应的小波函数为和 ${\psi }_{g,2}\left(t\right)$ 。

现在对同组的两个小波函数互相迁移半个单位，即

$\{\begin{array}{c}{\psi }_{h,1}\left(t\right)={\psi }_{h,2}\left(t-0.5\right)\\ {\psi }_{g,1}\left(t\right)={\psi }_{g,2}\left(t-0.5\right)\end{array}$ (2-4)

同时两组小波函数满足Hilbert变换对，

$\{\begin{array}{c}{\psi }_{g,1}\left(t\right)=H\left({\psi }_{h,1}\left(t\right)\right)\\ {\psi }_{g,2}\left(t\right)=H\left({\psi }_{h,2}\left(t\right)\right)\end{array}$ (2-5)

上述的尺度函数和小波函数构成了如下所示的复尺度函数和复小波函数，

$\varphi \left(t\right)={\varphi }_h\left(t\right)+j{\varphi }_g\left(t\right)$ (2-6)

$\{\begin{array}{c}{\psi }_1\left(t\right)={\psi }_{h,1}\left(t\right)+j{\psi }_{g,1}\left(t\right)\\ {\psi }_2\left(t\right)={\psi }_{h,2}\left(t\right)+j{\psi }_{g,2}\left(t\right)\end{array}$ (2-7)

3. 基于双密度双树复小波变换的图像压缩

3.1. 图像质量评价标准

在评价图像质量时，一般可以采用比较PSNR (峰值信噪比)来进行，PSNR的值越高就意味着图像的质量越好。PSNR的定义式为

$\text{PSNR}=10\log \left(\frac{{255}^2}{MSE}\right)$ (3-1)

其中MSE定义为

$MSE=\frac{1}{w\times h}{\displaystyle \underset{i=0}{\overset{w-1}{\sum }}{\displaystyle \underset{i=0}{\overset{h-1}{\sum }}{\left(a\left[i\right]\left[j\right]-b\left[i\right]\left[j\right]\right)}^2}}$ (3-2)

在式(3-2)中，w，h分别是图像的宽和高，而 $a\left[i\right]\left[j\right],b\left[i\right]\left[j\right]$ 分别是原始图像数据和重构图像数据。在此采用的原始图像是 $512\times 512$ 的灰度图像，计算重构后所得到图像的PSNR。

3.2. 实验结果比较和分析

本次实验选用比较有代表性的Lena图，在MATLAB仿真实验中结合小波工具箱使用双密度双树复小波变换对Lena图进行压缩，并和JPEG标准压缩进行对比。依次对Lena图分别压缩不同的倍数(在此依次选取4、8、16、32、64倍压缩)获得重构图像以及PSNR值。实际比较结果如图1~图3所示：

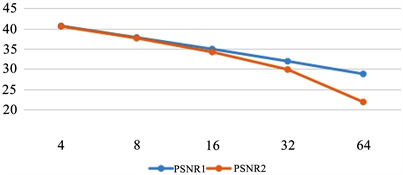
Figure 1. PSNR value comparison diagram of the two compression methods

图1. 两种压缩方法的PSNR值对比图

Figure 2. Compression Lena graph based on dual density dual tree complex wavelet transform

图2. 基于双密度双树复小波变换压缩Lena图

Figure 3. JPEG standard compressed Lena

图3. JPEG标准压缩Lena图

在图1中，PSNR1是基于双密度双树复小波的图像压缩的PSNR值，PSNR2是JPEG标准压缩的PSNR值。

综合以上的实验结果不难得出结论，采用双密度双树复小波变换后，重构图像的PSNR值比JPEG标准的更高，主观上看重构图像的效果明显更好。因此，基于双密度双树复小波变换的图像压缩效果和压缩质量都是比较好的。

4. 总结

基于小波变换的图像压缩方法，关键的一步是小波基函数的选择，选择不同的小波基函数来进行图像压缩所取得的压缩效果一般都不一样，本次选择的是双密度双树复小波变换，在理论上探究了利用双密度双树复小波变换来进行图像压缩所拥有的优势，通过对比实验结果验证了选取双密度双树复小波变换进行图像压缩确实有较好的效果。由于小波基函数数量庞大，用于图像压缩的最优小波基函数往往极难选取，同时还没有找到可以完全利用各种不同小波变换的所有统计特性的方法，因此基于小波变换的图像压缩方法还有很多值得研究的地方。