基于双种群协同进化遗传算法的电力仓库货位分配方法

Slotting Optimization in Automated Power Warehouse Based on Double-Population Co-evolutionary Genetic Algorithm

摘要: 针对电力自动化立体仓库出入库效率和高层货架稳定性问题，建立了多目标货位分配优化模型。提出了一种基于精英保留策略的双种群协同进化遗传算法并用于求解该模型。仿真实验结果验证了该算法比标准遗传算法具有更好的收敛性，能够有效提高物料出入库效率和货架的稳定性。

Abstract: Slotting optimization greatly affects the efficiency of automated power warehouse. This paper con-structs a multi-objective model of slotting optimization which takes warehousing efficiency and high-rise shelf stability into account. A Double-Population Coevolutionary Genetic Algorithm (DPCGA) based on elite retention strategy is proposed to solve the problem. The simulation result shows that DPCGA is practical and effective. It has better convergence and can effectively improve the efficiency of material storage and shelf stability.

1. 引言

电力行业是国家重要的基础能源行业，电力企业中发展使用先进的物资管理仓库，是电力物资顺畅流通的有力保障，优化仓储管理，降低仓储成本，提高仓储效率是仓储优化的重要任务。而合理的货位分配与设置是提高仓储效率的关键。

Malmborg [1] 在研究立体仓库时，指出不同的货位分配对取货平均费用有影响，在货物存取过程中通过计算存储空间的变化，比较不同货位分配策略下产生的费用成本，并描绘出费用分布概率函数。Onut [2] 主张构建起多层次的货架，依据不一样物品的周转率，来明确相关物品所储存的具体位置，并用粒子群算法(PSO)来求解这个问题。Muppani [3] 以存储空间最小化和拣选总成本最小化为优化目标，依托于分类存储法创建了非线性数学模型，并运用分支界定法进行求解。指出分类存储法在压缩搬运成本与节约仓储空间上优势突出。Henn [4] 对人工拣选作业仓库展开了研究，指出最小化搬运距离的函数模型可以借助禁忌搜索算法来求解，获得了较好的优化效果。Xie Jing [5] 采用分组约束的方法(SLAP-GC)对货物储存位置分配问题进行了研究，并利用有效制约邻域禁忌搜索(RNTS)算法求解储存位置分配方案。国内郑凌莺等 [6] 运用了“类聚”的概念和方法处理同系列产品就近存储的问题，从而实现物流中心的货位优化分配；陈月婷等 [7] 对自动化立体库分区和货位分配策略进行了研究，在仓库分区优化的基础上，提出了货位优化模型，并采用改进的Pareto遗传算法对模型进行求解；邱建东等 [8] 提出了应用遗传算法来优化周期性病毒货位分配优化；张贵军等 [9] 提出一种精英多策略差分进化算法，以货架重心低、出入库频率高、货物离出入库口近等为原则建立货位分配优化模型并求解。

综上可知，众多学者针对货位分配进行了大量的研究，但是在求解过程中多以单一群智能优化算法求解模型，易陷入局部最优，出现早熟收敛。本文以电力自动化立体仓库为研究对象，建立了基于货架稳定性、出入库效率为目标的优化模型，设计了一种结合精英保留策略、协同进化思想的双种群协同进化遗传算法。该算法将遗传算法进化种群划分为主、从种群，主种群加快算法收敛，从种群加入随机个体，保证了种群的多样性，从而提高了搜索能力。仿真实验验证了模型和算法的有效性。

2. 模型构建

自动化立体库也常被称为高层自动化仓库或者自动仓储AS/RS (AS/RS: Automated Storage and Retrieval System，自动存取系统)。它主要由仓库建筑体、立体式货架、托盘、堆垛机、输送系统、控制系统和计算机管理系统等部分组成，通过高层货架、巷道堆垛机和辊子输送机等机械化、自动化设备以及配电柜、托盘等辅助设备，运用货物条码、RFID技术和计算机控制等信息化技术进行仓储作业。

电力自动化立体仓库的存储系统决定了整个仓库的运行效率。成功的货位分配策略可以提高存储空间利用率，缩短仓库堆垛机移动的距离从而减少作业时间，而且可以减缓存储系统的磨损速度。

根据电力自动化立体仓库实际运行情况，有以下假设：

1) 假设货架有a排b列，每排货架有c层，每层可容纳d个货位，为方便计算，将每个货位的长度、高度和宽度归一化为单位1。将第x排y层第z列的货位标记为(x, y, z), x = 1, 2, 3, $\cdots$ , a; y = 1, 2, 3, $\cdots$ , b; z = 1, 2, 3, $\cdots$ , c。设置离出入口最近的一排为第1排，离出入口最近的一列为第1列，离地面最近的一层为第1层。

2) 假设仓库中可以存放Ｎ种不同的货物，相同种类的物品可以合并托盘放在同一货位中(大小不得超过货位容量)，不允许同一货位中存放不同类型的货物。

3) 假设每种货物的重量用M表示，货物的周转率用P表示，即某货物在一定时间内的周转次数为P。

4) 每两排货架间有一巷道，巷道中有一台堆垛机。定义水平x方向、Y方向运动速度分别是V_x和V_y；在垂直方向即Ｚ方向上运行速度为V_z。

2.1. 出入库效率原则

为了提高出入库效率，周转率高的物料应该离出入口较近从而使得总体的出入库时间较短。假设堆垛机取货时间可忽略，对于位于x排y列z层的货位(x, y, z)上的某货物，其出入库时间可简化为堆垛机

运行时间，即 $\frac{x}{v_x}+\frac{y}{v_y}+\frac{z}{v_z}$ 。仓库在一定周期内的出入库效率可用以下函数表示：

$f_1={\displaystyle \underset{x=1}{\overset{a}{\sum }}{\displaystyle \underset{y=1}{\overset{b}{\sum }}{\displaystyle \underset{z=1}{\overset{c}{\sum }}\left(\frac{x}{v_x}+\frac{y}{v_y}+\frac{z}{v_z}\right)\cdot p_{x,y,z}}}}$

2.2. 货架稳定性原则

为了保持仓库货架的稳定性，按照上轻下重、降低重心的原则，仓库货架的总重心可表示为f₂：

$f_2=\frac{{{\displaystyle \sum }}_{x=1}^a{{\displaystyle \sum }}_{y=1}^b{M}_{x,y,z}\cdot z}{{{\displaystyle \sum }}_{x=1}^a{{\displaystyle \sum }}_{y=1}^b{M}_{x,y,z}}$

联立以上目标函数，可得货位优化模型为：

$\{\begin{array}{l}\min f_1=\underset{x=1}{\overset{a}{{\displaystyle \sum }}}\underset{y=1}{\overset{b}{{\displaystyle \sum }}}\underset{z=1}{\overset{c}{{\displaystyle \sum }}}\left(\frac{x}{v_x}+\frac{y}{v_y}+\frac{z}{v_z}\right)\cdot p_{x,y,z}\hfill \\ \min f_2=\frac{{{\displaystyle \sum }}_{x=1}^a{{\displaystyle \sum }}_{y=1}^b{M}_{x,y,z}\cdot N_{x,y,z}\cdot z}{{{\displaystyle \sum }}_{x=1}^a{{\displaystyle \sum }}_{y=1}^b{M}_{x,y,z}}\hfill \end{array}$

$s.t.\{\begin{array}{c}1\le x\le a\\ 1\le y\le b\\ 1\le z\le c\\ x,y,z\in Z\end{array}$

显然，这是一个多目标优化问题，通过对设置权重，可将多目标问题转化成单目标问题：

$f={\varpi }_1\underset{x=1}{\overset{a}{{\displaystyle \sum }}}\underset{y=1}{\overset{b}{{\displaystyle \sum }}}\underset{z=1}{\overset{c}{{\displaystyle \sum }}}\left(\frac{x}{v_x}+\frac{y}{v_y}+\frac{z}{v_z}\right)\cdot p_{x,y,z}+{\varpi }_2\frac{{{\displaystyle \sum }}_{x=1}^a{{\displaystyle \sum }}_{y=1}^b{M}_{x,y,z}\cdot N_{x,y,z}\cdot z}{{{\displaystyle \sum }}_{x=1}^a{{\displaystyle \sum }}_{y=1}^b{M}_{x,y,z}}$

其中 $0\le {\varpi }_1\le 1，0\le {\varpi }_2\le 1且{\varpi }_1+{\varpi }_2=1$ 。

3. 算法设计

在标准遗传算法(Standard Genetic Algorithm, SGA)中，所有个体构成的种群是一个不可分割的整体，遗传操作算子作用在整个种群上。单种群遗传操作策略对初始参数较为敏感，算法收敛性能差，容易早熟、陷入局部最优。为了提高遗传算法效率，Tsutsui [10] 提出了种群分裂(forking)的思想用于多峰优化问题中寻找多个峰值。多种群遗传算法(Multi-population Genetic Algorithm, MPGA)随之发展而来。它在遗传算法并行运算的基础上，采用多个种群进行协同进化。对于不同的种群，采用不同的遗传操作参数组合来控制种群的进化，而且，各种群之间并不是相互独立的，它们通过移民算子来实现种群之间的信息交换，以实现搜索种群染色体个体的多样性，达到全局搜索的效果，避免未成熟收敛问题。

本文提出的双种群协同进化遗传算法(Double Population Genetic Algorithm, DPGA)将种群划分为主、从两个种群，两个种群按照不同的策略来完成各自的进化。主种群用于加快算法收敛，采用适应值共享策略，在选择过程中采用轮盘赌选择策略并结合了精英保留策略，也可视为精英种群；从种群的进化目标是提高种群的搜索能力，需要尽量维持较高水平的多样性，选择策略使用锦标赛选择策略，同时采用随机移民策略来维持种群个体的多样性，也可视为普通种群。算法描述如下：

Step 1：初始化：t = 0，种群规模N，随机初始化种群 $P_S\left(t\right)$ ， $P_S\left(t\right)$ 计算种群的适应度值，将种群按适应度值降序排列；

Step 2：选择前M个优秀个体作为精英库 $Best\left(t\right)$ 成员；

Step 3：记录 $P_M\left(t\right)$ 中的最优个体M-elite (t)，记录 $P_S\left(t\right)$ 中的最优个体S-elite (t)，并用S-elite (t)替换 $P_M\left(t\right)$ 中适应值最小的个体；

Step 4：主种群 $P_M\left(t\right)$ 经适应值共享后选择产生子种群 $P_M\left(t+1\right)$ 并对 $P_M\left(t+1\right)$ 执行交叉、变异操作；

Step 5：对精英库 $Best\left(t\right)$ 中的每个个体 $Bes{t}_i\left(t\right)$ ， $\left(i=1,2,\cdots ,\text{M}\right)$ ，分别与M-elite (t)执行交叉和变异操作，得到新个体 $Bes{t^{\prime }}_i\left(t\right)$ ，若新个体的适应度值大于M-elite (t)的适应度值，则替换掉 $P_M\left(t+1\right)$ 中适应度值最小的个体；

Step 6：记录 $P_M\left(t+1\right)$ 中的最优个体M-elite (t + 1)，若其优于 $Best\left(t\right)$ 中的最优个体，则用M-elite (t + 1)取代 $Best\left(t\right)$ 中的最差个体，得到更新后的精英库 $Best\left(t+1\right)$ ；

Step 7：在从种群 $P_S\left(t\right)$ 中选出种群 $P_S\left(t+1\right)$ 进行交叉、变异等演化操作；

Step 8：更新种群；

Step 9：判断是否满足终止条件；若是，则结束；否则转到Step 3。

3.1. 编码设计

在电力自动化立体仓库中，所有物品需要通过托盘入库并依托于托盘存放在某一货位上。也就是说入库操作就是为托盘寻找合适货位并通过堆垛机存放在该货位上。考虑到入库时可选货位数量是固定的，我们选择整数编码的方法，每个个体的编码表示一种可行的货位分配方案：用数字所在位置表示货位，数字表示托盘编号，无托盘货位上设置为0，从而形成一条染色体，染色体长度为可选货位的数量。

3.2. 种群初始化

遗传算法的最终结果会受到种群规模的影响。种群规模越大其代表性就越强，优化的幅度就越大；种群规模越小其代表性就越差，优化的幅度就越小。但同时，种群规模越大，其计算过程就会越复杂。一般在设计遗传算法时会将种群规模控制在50~500之间，这样既可以保证种群的多样性又可以避免计算过程太复杂。

种群初始化方法为随机生成一定数目的个体来作为遗传算法初始种群。在本文应用实例中，设定空闲货位数目为K，将入库的L个托盘依次编号为1~L，初始种群为由1~L及(K-L)个0随机排列组成的长度为K的数组。

3.3. 适应度评价函数

适应度是遗传算法描述个体性能的重要指标，算法根据适应度的大小对个体进行优胜劣汰，适应度越大的个体遗传到下一代的概率就越大。

根据建模过程中得到的函数模型，电力仓库货位优化问题为求函数的极小值问题，因此，可采用原目标函数加1后取倒数来形成适应度函数，即：

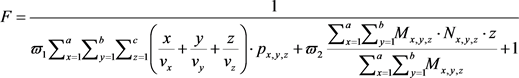
3.4. 遗传进化运算

3.4.1. 选择运算

选择运算是体现了“适者生存”原理，通过适应度评价选择出优质个体。在主种群选用轮盘赌选择(Roulette wheel selection)方法，即个体被选中的概率取决于该个体的相对适应度。第i个个体的相对适应度如下式所示：

$p_i=\frac{F_i}{{{\displaystyle \sum }}_1^N{F}_i}$

其中，F_i为第i个个体的适应度，N为种群中个体总数， ${\displaystyle {\sum }_1^N{F}_i}$ 为所有个体总适应度。

执行选择操作时，随机生成一个数 $R\in \left[0,1\right]$ ，若 $0\le R\le p_1$ ，则选择个体1； $p_{i-1}\le R\le p_i\left(i>1\right)$ ，则选择个体i。

在从种群使用锦标赛选择策略(Tournament Selection)。锦标赛选择策略是遗传算法中最为流行的选择策略。其思想是在整个种群中每次选取n个个体，以适应度值为度量参与竞争(即锦标赛)，从中选择适应值最高的个体作为新一代群体中的个体，重复这样的操作直到个体数达到群体规模。通常情况下取n = 2，也被称为二元锦标赛选择(Binary Tournament Selection)。

3.4.2. 交叉运算

交叉运算是指对两个父代个体中部分基因相互交换从而形成子代个体。设交叉概率为 $p_c$ ，将两个父代个体上随机两个位置之间的基因进行交换，并调整使其余基因合法，即可得到两个子代个体。在本文中使用Order Crossover (OX)。该交叉运算的主要步骤如下：

首先随机选择一对染色体(父代)中几个基因的起止位置(两染色体被选位置相同)：

第二步，生成一个子代，并保证子代中被选中的基因的位置与父代相同：

第三步，先找出第一步选中的基因在另一个父代中的位置，再将其余基因按顺序放入上一步生成的子代中：

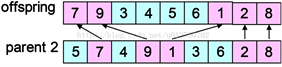
3.4.3. 变异运算

本文采用基本位变异法实现变异运算。设变异概率为 $p_m$ ，考虑到个体的合法性，当个体满足变异条件时，随机选择变异点和交换点，直接交换位于变异点和交换点上的两个基因，从而形成合法的子代个体。

4. 实验仿真与分析

对于江苏某电力自动化立体仓库，该仓库配备高层立体货架共有6排20列4层，共计480个货位，水平方向使用传送带，垂直方向使用巷道式堆垛机，仓库和货位的相关参数见表1：

Table 1. Automatic three-dimensional warehouse operation parameters

表1. 自动化立体仓库运行参数

为了方便计算，假设传送带和堆垛机以恒定速度运行，启动和拣选物料的时间忽略不计。

以该仓库在2018 年7 月的运行数据为例，该月份上下架物料如表2所示，某次入库初始空闲货位信息如表3所示，待入库托盘信息如表4所示。

Table 2. Material data of upper and lower shelves

表2. 上下架物料数据

Table 3. Initial free cargo location information

表3. 初始空闲货位信息

Table 4. Incoming pallet information

表4. 待入库托盘信息

为了验证DPGA的有效性，运用DPCGA和SGA分别对模型进行求解，取交叉概率 $p_c=0.7$ ，变异概率 $p_m=0.01$ ，初始种群规模设为50，最大迭代次数为500，DPCGA中精英种群规模为25，将DPGA和SGA分别重复运行30次，记录每一次迭代中的最优适应度值，得到两种算法的平均收敛曲线如图1所示。为了衡量解的质量和算法的稳定性，计算多次重复运行条件下所得最优解的平均值和均方差如表5所示。

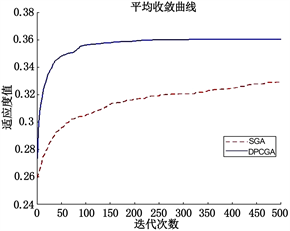
Figure 1. The optimal fitness value iteration curve

图1. 最优适应度值迭代曲线

Table 5. Algorithm stability and effectiveness

表5. 算法稳定性和有效性

如表5所示，DPCGA多次重复运行得到最优解的最大值和最小值相等，即每次重复运行可以得到同样的最优解。这说明了DPCGA对初始种群不敏感，能够稳定的收敛于全局最优解。而SGA在不同的初始条件下获得的解不一定能收敛于全局最优解，对初始种群较敏感，容易陷入局部最优。同时由图1可见，DPCGA在100次迭代以后就可以稳定，而SGA需要迭代400次以上。也就是说，DPCGA能够更快的收敛到最优解，而且相对SGA而言获得解更稳定，这是由于DPCGA引入了精英保留策略，较不容易丢失较优解，总体来讲更容易获得高质量的最优解。可见DPCGA在收敛速度、解的质量等方面均优于SGA。

5. 结束语

货位规划与分配是仓库作业的重要环节，合理的货位规划与分配是有效提高仓库作业效率的关键手段之一。本文以电力自动化立体仓库为研究对象，对货位分配方案进行了研究。首先，通过分析货物重量对货架稳定性的影响，以及货物的出入库频率和到达货位所需的时间对出入库作业效率的影响，建立了货位分配优化模型；然后提出了一种基于双种群协同进化的遗传算法对模型进行求解。最后，通过实验对模型及其求解方法进行了有效性验证。结果表明，该算法较标准遗传算法更快收敛，能更稳定的获得较好的最优解。