农业传感网络数据差错分析算法研究

Research on Data Error Analysis Algorithm of Agricultural Sensor Network

摘要: 农业气象观测要素精度的高低对观测效果有着重要影响，尤其是在野外复杂的环境下，影响温度变化的要素尤其多。目前大量用于野外温度观测的设备多为节点分散的无线传感网络，所用传感器为成本低、精度差的工业传感器，一旦出错，难以排查，且对后续分析工作影响巨大。为了降低出错无线传感器的排查难度，及时锁定出错数据，从农业传感网络数据的角度入手，对其进行差错分析，从而对野外的无线传感网络进行出错排查。通过对自动站的标准数据进行充分提取分析，发现以一年为周期，同一天不同地区之间的最高温度差成近似正态分布，类比自动站所采集的温度数据特性，通过对工业传感器采集的数据进行提取、平滑等分析，发现了该性质也适用于工业传感器，由此设计了一种数据差错分析算法，应用于野外的工业传感器的检错，通过温度这一农业气象观测的关键要素之一进行验证，验证结果证明了该算法的有效性。该检错方法不直接对现有无线传感网络进行操作，而是对其进行数据无量纲化处理，再对其进行提取、平滑和对比等处理来检错，节省了传感器检错成本，节省人力物力。

Abstract: The accuracy of the agrometeorological observation elements has an important impact on the observation effect, especially in the complex environment of the field, especially the factors affecting the temperature change. At present, a large number of devices for field temperature observation are mostly wireless sensor networks with scattered nodes. The sensors used are low-cost, low-precision industrial sensors. Once they are in error, they are difficult to check and have a great impact on subsequent analysis. In order to mitigate the difficulty in searching the dysfunctional wireless sensors and targeting the problematic data, we analyze error from the perspective of agricultural sensor network data, and subsequently check out the errors in the wild wireless sensor network. By fully extracting and analyzing the standard data of the automatic station, it is found that the maximum temperature difference between different regions on the same day is approximately normal distribution on a one-year cycle, and the temperature data characteristics collected by the analog automatic station are collected by industrial sensors. The data were extracted and smoothed, and it is found that this property is also applicable to industrial sensors. Therefore we design a data error analysis algorithm, applied to wild industrial sensor calibration. By validating temperature, which is one of the essential factors in agricultural atmosphere observation, the result demonstrates the efficiency of the algorithm. Instead of directly manipulating on the current wire-less sensor network, the algorithm conducts dimensionless processing, followed by extraction, smoothing, and comparison to inspect error, to save the cost of error inspection.

1. 前言

我国是农业大国，农业气象观测是我国农业气象服务的基础，也是地面观测的重要环节 [1] 。农业气象观测数据的质量直接影响到作物的生命活动以及野外农业气候预测的准确性，同时也影响着作物的品质和产量以及病虫害的预防工作。随着我国社会经济和科学技术的不断发展，“高产、优质、高效”已经成为我国农业新的发展方向，这也就对气象为农服务提出了更高的要求，高精度、高密度、多要素、连续稳定的农业气象观测信息是现代农业快速发展基本保证 [2] 。

随着传感器和无线通信技术的不断进步，现在的无线传感网络也大多由一些低功耗、体积小、功能多的传感器组成。但这种廉价微型的传感器，在野外复杂的环境下，容易造成磨损和测量不准，故传感器的检错至关重要 [3] 。本文选取温度要素进行观测，提出一种通过对农业气象观测数据进行分析检测对应传感器的方法。

2. 我国农业气象观测现状

自20世纪50年代开始，我国开始建设农业气象观测网，至2009年我国共有农业气象观测站631个，其中一级农业气象观测站398个，二级农业气象观测站233个，另外还有68个农业气象试验站 [4] 。1979年编制和出版了《农业气象观测规范》并在1993年对其范进行了修订 [5] 。但我国的农业气象观测体系是上世纪建立的，观测仪器设备老旧落后，多数农业气象观测任务需要人工手动操作，不仅费时费力，还消耗了大量的人力物力，造成观测任务的成本较高。为与现代农业发展相适应，自2009年开始，我国开始大量组建自动化农业气象观测网，大力推动自动化农业气象观测的发展 [6] 。随着农业技术的快速发展，气候的不断变化以及农业种植生产模式的不断改进，以往的农业气象观测模式无论是在站点布局、观测重点、观测频率以及精度上都已经无法满足现代农业发展日益提高的需求。因此，农业气象观测已经成为我国重点关注的问题之一。

3. 无线传感网络与观测要素的地域特征

随着自动气象站的推广和普及，农业气象观测相关技术已近成熟，但对于数据获取的规模和数据的分辨率方面能力还是比较有限的。这是由于自动气象站用于获取数据的设备都是一些价格昂贵高度精密仪器，具有远距离传输功能的无线通讯设备，而这些设备不可能高密度的部署，所以大多数农业自动气象站点的布局是非常广泛的，那么在监测作物生育期时想要做到精准化控制是远远不够的 [7] 。这时无线传感器网络的优势就得以体现了，大量传感器节点共同协助，收集周围的环境信息，可以包括温度，光照强度，降水量，定位等类似的信息 [8] 。本文通过对自动站采集的数据进行分析，并将找到的规律迁移到工业传感器的检错上，选取温度数据进行验证，达到不直接对工业传感器进行操作而是通过数据分析进行检错。

3.1. 观测要素验证的确定

通过对野外环境农业气象要素的观测，不仅可以有效的避免突发自然环境变化对作物的影响，精准全面的数据采集还可以为农业精准化控制提供基础，使作物常年处于最佳的生长条件。作物品种不同对与环境要求也不同，同一作物处于不同生长阶段要求的适宜环境也存在差异。本文选取对作物生长最为关键要素之一进行验证——温度。

温度：温度是对作物生长影响最多的要素之一。它主要通过光合作用、呼吸作用、蒸腾作用来影响作物生长。野外内气温分布并不是均匀的。作物的光合作用需要有一定温度范围及三基点，即作物生长过程中的最适温度、最高温度和最低温度 [9] 。当野外温度超出范围时就会影响作物的生长。三基点会随着作物生长的不同阶段而变化，如：生长前期，作物所需温度较高，否则会出现茎细叶薄的现象；生长后期，为保证果实率则需要较低的温度 [9] 。

3.2. 温度的地域特征挖掘

由于观测手段的逐步改善，在同一要素的数据记录上存在较大差异 [10] ，故选取观测手段一致的1971年到1980年间的A、B两地每天的最高温度数据作为分析的基本要素，以年为周期对不同地区同一天的最高温度差，以0.1为步进做统计计数，再对结果进行小波变换，做无量纲化处理，再进行提取、平滑、分析等处理来挖掘温度所具有的地域特征。

日高温度差：

$D_{A_n{B}_n}=T_{A_n}-T_{B_n}$ (1)

其中 $T_{A_n}$ 和 $T_{B_n}$ 分别代表A、B两地的日最高温度， $D_{A_n{B}_n}$ 代表A与B地之间的日最高温度差，其中平年的，闰年的 $1<n<366$ 。

统计计数：再−2.5℃到2℃之间，以0.1℃为步进，统计频数。

小波变换：是一个时间和频域的局域变换的时频分析方法，能有效地从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析，主要特点是通过变换能够充分突出问题某些方面的特征 [11] ，这里主要采用基于小波变换的多尺度空间中模极大值特征的提取方法，利用小波变换的信号局域化分析能力，求解小波变换的模极大值特征来检测信号的局部奇异值，即突显出日最高温度差频数的众数区间。小波是一个均值为零，且既在时域又在频域存在的函数。小波变换有很多种，这里用到的是离散小波变换(DWT)，其小波基函数为：

${\Psi }_{a,\tau }\left(t\right)=\frac{1}{\sqrt{a}}\Psi \left(\frac{t-\tau }{a}\right)$ (2)

其中a、τ限定在一些离散的点上取值。

对尺度进行幂级数离散化，令： $a=a_0^j,a_0>0,j\in Z$

则，此时小波基函数为：

${\Psi }_{a,\tau }\left(t\right)=a_0^{\frac{-j}{2}}\Psi \left[a_0^{-j}\left(t-\tau \right)\right],j=0,1,2,\cdots$ (3)

位移离散化：

$\tau =k{a}_0^j{\tau }_0$ (4)

故离散小波变换可以定义为：

${\text{WT}}_f\left(a_0^j,k{\tau }_0\right)={\displaystyle \int f\left(t\right){\Psi }_{a_0^j,k{\tau }_0}^{*}\left(t\right)\text{d}t},j=0,1,2,\cdots ,k\in Z$ (5)

无纲量化：取 $a_0=2$ ， ${\tau }_0=1$ ，则小波基为：

${\Psi }_{j,k}\left(t\right)=2^{-\frac{j}{2}}\Psi \left(2^{-j}t-k\right)$ (6)

对应的小波离散变换为：

${\text{WT}}_f\left(j,k\right)={\displaystyle \int f\left(t\right){\Psi }_{j,k}^{*}\left(t\right)\text{d}t}$ (7)

提取：对与10年的日最高温度差频数进行分析，提取固定存在的地域特性，并找出频数最大的最高气温差区间作为两地最高气温差的回归区间。

平滑：为了更好的查看数据走向、查看数据趋势 [12] ，我们采用曲线五点滑动平均方法对日最高温度频数进行平滑处理，来提高数据的光滑度，其公式如下：

非端点：

$x\left(n\right)=\frac{x\left(n-2\right)+x\left(n-1\right)+x\left(n\right)+x\left(n+1\right)+x\left(n+2\right)}{5}$ (8)

端点：

$x\left(1\right)=\frac{3x\left(1\right)+2x\left(2\right)+x\left(3\right)-x\left(4\right)}{5}$ (9)

$x\left(2\right)=\frac{4x\left(1\right)+3x\left(2\right)+2x\left(3\right)+x\left(4\right)}{10}$ (10)

$x\left(m-1\right)=\frac{x\left(m-3\right)+2x\left(m-2\right)+3x\left(m-1\right)+4x\left(m\right)}{10}$ (11)

$x\left(m\right)=\frac{-x\left(m-3\right)+x\left(m-2\right)+2x\left(m-1\right)+3x\left(m\right)}{5}$ (12)

其中， $x\left(n\right)$ 表示最高温度频数序列， $3\le n\le m-2$ ，m为数据总个数。

4. 仿真结果及特性分析

4.1. 模型建立与仿真

使用Matlab结合Microsoft Excel建立模型并挖掘。自动站分析模型建立框架如图1所示，对自动站资料进行最高温度差和频数分布的计算，通过离散小波变换进行无量纲化处理，再进行平滑处理以便分析趋势与提取特征。同理工业传感器验证模型框架如图2所示。采用相同分析方法对工业传感器资料进行处理，类比由自动站资料得出的结论，进行特征分析。如图3所示为检错流程图，首先将两地的数据载入模型，对数据进行日最高温度差及其频数的计算，在通过离散小波变换对其进行无量纲化处理，选择合适的平滑系数进行特性分析，若满足地域特性的要求则两组数据是正确的，若无明显地域特性则说明采集的数据有误。原始数据为Excel格式，A、B两地情况分别如表1、表2所示，使用excel计算 $D_{A_n{B}_n}$ ，得到下表3。

Table 1. A point daily maximum temperature table

表1. A地日最高温度表

Table 2. B point daily maximum temperature table

表2. B地日最该温度表

Table 3. Maximum temperature difference between A & B

表3. A-B地最高温度差

Figure 1. Automatic station analysis model framework

图1. 自动站分析模型框架

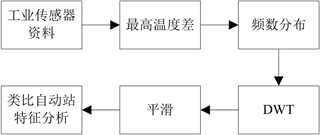
Figure 2. Industrial sensor validation model framework

图2. 工业传感器验证模型框架

Figure 3. Error detection flow chart

图3. 检错流程图

4.2. 特性分析

如图4所示为，自动气象站测得的最高温度差的频数分布图，从图中可以看出每一年的最高温度差频数分布都呈近似正态分布，并大致保持一致的趋势。对以下几个参数进行分析：

趋势：每条曲线都呈现近似正态分布的趋势，且均存在一个最高值，代表一年中此点对应最高温度差的频数最大，也就是说一年之中有一部分时间的日最高温度差均为一固定值，即为最高温度差的可回归的地域特性提供了依据。

半高宽：又称半峰宽(Full Width at Half Maximum)，这里指的是以频数曲线高度最大处为中心，当高度为一半时曲线的全宽，即峰值高度一半时的最高温度差跨度。对每一年的频数曲线求半高宽，再取交集，可以得出[−1℃~0℃]囊括了一年中大部分时间的最高温度差，可作为最高温度差地域特性的回归区间。

Figure 4. Frequency distribution curve of the highest temperature difference between A and B

图4. A、B两地最高温度差的频数分布曲线

4.3. 检错可行性验证

选取两个具有差异的环境点C、D，每个点各放置两个工业传感器T1、T1’、T2、T2’，假设每个点放置的工业传感器完全相同，且其中T1、T1’保证读数准确，T2、T2’为不准传感器，其测试环境如图5所示。读取两个环境点放置的工业传感器采集的日最高温度数值，计算两个环境点之间的最高温度差，并进行分析，确定其地域特性是否存在回归区间，如图6所示为检错判定流程图。

Figure 5. Industrial sensor test environment diagram

图5. 工业传感器测试环境示意图

Figure 6. Error detection decision flow chart

图6. 检错判定流程图

经过Matlab仿真测试，得到如下结果图7。从图中可以看出蓝色线为T1组传感器，即准确传感器组测得的两个环境点最高温度参数差的频数分布曲线，可以看出两环境点间存在一个频数最大的温度差，可以取[0℃~1℃]作为回归区间。图中红色线为T2组传感器，即不准传感器组测得的两个环境点最高温度参数差的频数分布曲线，由图可看出曲线整体起伏不大并未有明显最高点，无法找到回归区间，故怀疑这组数据有误。

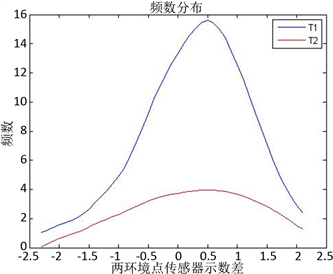
Figure 7. Error detection test result chart

图7. 检错测试结果图

5. 总结与展望

本文选取观测手段一致的计量级传感器测得的日最高气温数据入手，挖掘温度存在的地域性特征，并应用该特征设计了一种数据差错分析算法用于提高野外工业传感器检错效率，节约检测成本。该算法提供了一种全新的农业传感网络检错视角，在一定程度上推进了现代农业的数据化发展 [13] ，但依然存在很多可以深入研究的地方，未来的研究方向可以从以下几个方面入手：

1) 数据的利用：由于数据的差异型，本文只用了人工观测的数据，未来可以从自动站与人工检测的数据同步方向入手，将自动站的数据进行相应的平滑、筛选、补偿处理，将其与人工观测的数据结合起来分析。

2) 工业传感器的矫正：本文仅是提供了通过数据检测传感器好坏的方法，但对于出错数据的矫正方法仍有待研究，如可以采用游走拓扑等方式。

3) 工业传感器的精度提升：在本文提出的检测方法基础上，可以利用最高温度差的回归特性，将工业传感器向计量传感器的精度进行修正，使成本低的工业传感器经过数据修正达到计量级精度。