1. 引言
一般来说,如果我们能把一个n次曲面分类成功,并得到其所有的标准方程,那么可以认为我们对这种曲面就认识清楚了。如几何学家们把二次曲面分成了5类,并成功地给出了其所有的17个标准方程 [1] 。这样任意给定一个二次曲面的方程,我们就知道它一定是17个方程之一,因此,在某种意义上,二次曲面对我们来说就没有任何秘密可言。对于三次曲面,有众多学者从不同角度进行了研究并取得了丰硕的成果 [2] [3] [4] [5] ,其中Wanseok,Euisung等研究了在任意特征的k代数闭合场下非正规三次超曲面的分类 [4] ;Bruce,Wall等重建了复射影三次曲面的分类 [5] 。但到目前为止,还未见有文献对复合曲面进行了分类研究或给出了其标准方程。
复合曲面简单地说,就是多个函数乘积形成的方程所确定的曲面 [6] ,是生活中最常见应用最广的曲面,简单如书就是由多个平面复合而成,复杂一点如绝大多数建筑物也是由多个简单的曲面复合而成 [7] 。三次复合曲面是复合曲面中的重要组成部分,它由二次曲面与平面复合而成,是复合曲面中较基础的部分。本文为了对3次复合曲面的分类问题进行深入的系统的研究,先把平面分类,然后在此基础上,把3次复合曲面分类。把其分为了5个大类,50个小类,并且在不对平面方程中的系数区分正负号的条件下,得到了三次复合曲面的所有150个标准方程。
本文研究的曲面方程都是指实系数方程。
2. 已有成果
为了阅读方便,我们先罗列一些本文常用到的概念及成果:
定义2.1 [6] :由三元n (≥1)次方程
(1)
所表示的曲面叫做n次曲面,其中i,j及s都是非负整数,并且至少有一个n次项的系数不为0,其中
称为n次曲面函数。
当n = 2时,为了便于研究,通常把2次曲面的方程书写为
(2)
定义2.2 [1] :空间直角坐标变换的一般公式(直角坐标系的平移及转轴变换):
(3)
定理2.1 [1] :对二次曲面,通过适当选区直角坐标系,即进行恰当的直角坐标系的平移及转轴变换(3),二次曲面的一般方程(2)总可化为下列5个简化方程中的一个:
1)
2)
3)
4)
5)
。
定理2.2 [1] :适当选取坐标系,二次曲面的方程总可以写成下面十七种标准方程的一种形式:
(1)
(椭球面);
(2)
(虚椭球面);
(3)
(点或虚母线二次锥面);
(4)
(单叶双曲面);
(5)
(双叶双曲面);
(6)
(二次锥面);
(7)
(椭圆抛物面);
(8)
(双曲抛物面);
(9)
(椭圆柱面);
(10)
(虚椭圆柱面);
(11)
(相交于一条实直线的一对共轭虚平面);
(12)
(双曲柱面);
(13)
(一对相交平面);
(14)
(抛物柱面);
(15)
(一对平行平面);
(16)
(一对平行的共轭虚平面);
(17)
(一对重合平面)。
3. 三次复合曲面的分类
定义3.1:如果一个3次曲面能写成如下形式
(4)
其中
是2次曲面函数,
是一次曲面(即平面)函数,则称这个3次曲面为3次复合曲面(或可分的3次曲面);并分别称2次曲面
= 0与平面
为这个3次复合曲面的二次分曲面与分平面;如果不能,则称为不可分的3次曲面。
为了对三次复合曲面进行分类,下面先对平面的分类进行讨论:
定义3.2:设平面的一般方程为
(5)
其中实常数A,B,C不全为0。如果在交换变元x,y,z及重新命名平面系数A,B,C与D的条件下,不能化为同一形式的任意两个平面方程,称为不同类型的平面方程。
定理3.1:如果平面方程(5)中的变元x,y,z可以自由交换,则平面方程可以分为以下6类:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
证明:在方程(5)中,当A,B,C与D都不为0就是第(i)类;当A,B与C都不为0,且D为0,则化为第(ii)类;当A,B与C中有一个为0,而D不为0,则化为第(iii)类;当A,B与C中有一个为0,且D为0,则化为第(iv)类;当A,B与C中有两个为0,而D不为0,则化为第(v)类;当A,B与C中有两个为0,且D为0,则化为第(vi)类。毫无疑问,(i)~(vi)属于不同的类,因为他们相互间在交换变元x,y,z及重新命名平面系数A,B,C与D的条件下,不能互化。 □
定理3.2:适当选取坐标系,三次复合曲面的一般方程(4)总可化为下列5大类简化方程中的一个:
(I)
(II)
(III)
(IV)
(V)
其中A,B,C不全为0。
证明:根据3次复合曲面(4)的2次分曲面
的特点,由定理2.1知,适当选取坐标系,即进行恰当的坐标的转轴与平移变换(3),可以把
化为定理2.1中的5种形式,同时此变换把平面方程
化为了
形式。由于平面方程在任何坐标系下都是一次方程,因此A,B,C不全为0。所以,适当选取坐标系后,任一3次复合曲面(4)都可以化为本定理描述的5大类形式之一。 □
定理3.2的分类是在平面方程
中的系数A,B,C不全为0的条件下得到的,并没有考虑A,B,C及D的具体情况。为了得到标准方程,我们有必要加以考虑。由定理3.1知,平面
可以分为6类,是否意味着能利用乘法原理,得到由定理3.2的5大类扩展成30小类的结论呢?我们说不能,因为定理3.1有一个先决条件:能自由交换变元x,y,z,而定理3.2中的平面方程
中的变元及其系数是不自由的,是被动得到的,因此如果仅考虑A,B,C,D中有几个为0而不考虑他们的正负号的条件下,我们有
定义3.3:在定理3.2的5大分类方程中,如果进一步考虑A,B,C,D中有几个为0而不考虑他们的正负号的条件下得到的方程称为三次复合曲面(4)的小类方程;如果在交换变元x,y,z及重新命名二次分曲面函数系数aij (不同大类有不同的aij)与平面系数A,B,C的条件下,不能化为同一形式的两个小类方程称为不同类型的小类方程。
从而,在进一步考虑A,B,C,D中有几个为0而不考虑他们的正负号的条件下,我们有下面引理3.1~3.5:
引理3.1:适当选取坐标系,定理3.2中的(I)式可化为下列6小类简化方程中的一个:
(1-1)
(1-2)
(1-3)
(1-4)
(1-5)
(1-6)
其中
。
证明:在(I)式中的二次分曲面函数
关于
对称,使得
中的
可以自由交换,满足定理3.1的条件,因此组合分配一下就可得到本引理中的6类简化方程。 □
引理3.2:适当选取坐标系,定理3.2中的(II)式可化为下列10小类简化方程中的一个:
(2-1)
(2-2)
(2-3)
(2-4)
(2-5)
(2-6)
(2-7)
(2-8)
(2-9)
(2-10)
其中
。
证明:(2-1)与(2-2)是显然的,因为分平面函数关于
对称,因此只能形成这两个类。但(2-3)以下的方程与引理3.1中的(1-3)以下的有些不同,因为二次函数
仅关于
对称,关于x与
与z都不对称,且定理3.1中的(iii)式中的平面函数
也仅关于
对称,关于x与
与z不对称,因此x与z或y与z不能交换,这就造成(2-3)与(2-4)是不一样的类,因为通过交换变元及重新命名系数不能实现两个方程的互化,但曲面方程
,
,不是全新的类,因为它中的x与y交换,并重新命名系数就可以得到(2-4)。因此,在二次分曲面函数为
及平面函数
中的系数
中仅有一个为0的条件下,会产生两个完全不同的类(2-3)与(2-4)。同理我们可以得到(2-5)~(2-10)等6个不同的类。 □
引理3.3:适当选取坐标系,定理3.2中的(III)式可化为下列10小类简化方程中的一个:
(3-1)
(3-2)
(3-3)
(3-4)
(3-5)
(3-6)
(3-7)
(3-8)
(3-9)
(3-10)
其中
。
证明:与引理3.2的证明类似。 □
引理3.4:适当选取坐标系,定理3.2中的(IV)式可化为下列14小类简化方程中的一个:
(4-1)
(4-2)
(4-3)
(4-4)
(4-5)
(4-6)
(4-7)
(4-8)
(4-9)
(4-10)
(4-11)
(4-12)
(4-13)
(4-14)
其中
。
证明:(4-1)与(4-2)是显然的。二次分曲面函数
关于
都不对称,且定理3.1中的(iii)式中的平面函数
仅关于
对称,关于x与 与z不对称,因此总体而言,x与y,x与z或y与z都不能交换,因此(4-3)与(4-4)是不一样的;另外,与引理3.2不一样的是(4-5)
与z不对称,因此总体而言,x与y,x与z或y与z都不能交换,因此(4-3)与(4-4)是不一样的;另外,与引理3.2不一样的是(4-5) 是全新的类,因为通过交换变元及重新命名系数不能与(4-3)或(4-4)中的任意一个互换。同理我们可以得到(4-6)~(4-14)。 □
是全新的类,因为通过交换变元及重新命名系数不能与(4-3)或(4-4)中的任意一个互换。同理我们可以得到(4-6)~(4-14)。 □
引理3.5:适当选取坐标系,定理3.2中的(V)式可化为下列10小类简化方程中的一个:
(5-1) 
(5-2) 
(5-3) 
(5-4) 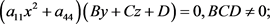
(5-5) 
(5-6) 
(5-7) 
(5-8) 
(5-9) 
(5-10) 
其中 。
。
证明:(5-1)与(5-2)是显然的。由于二次分曲面函数 仅关于y与z对称,且定理3.1中的(iii)式中的平面函数
仅关于y与z对称,且定理3.1中的(iii)式中的平面函数 关于
关于 对称,关于x与
对称,关于x与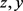 与z不对称,因此x与y及x与z都不能交换,这就造成(5-3)与(5-4)是不一样的类,因为通过交换变元及重新命名系数不能互换,但曲面方程
与z不对称,因此x与y及x与z都不能交换,这就造成(5-3)与(5-4)是不一样的类,因为通过交换变元及重新命名系数不能互换,但曲面方程 ,不是全新的类,因为它中的y与z交换,并重新命名系数就可以得到(5-3)。同理我们可以得到(5-5)~(5-10)。 □
,不是全新的类,因为它中的y与z交换,并重新命名系数就可以得到(5-3)。同理我们可以得到(5-5)~(5-10)。 □
定理3.3:适当选取坐标系,三次复合曲面的一般方程(4)总可化为引理3.1~3.5中的50小类简化方程中的一个。
证明:由引理3.1~3.5知。 □
4. 标准方程
本节将探讨3次复合曲面的所有可能的标准方程。这里我们对平面方程中的实系数A,B,C及D仅考虑他们是否为0,而不考虑他们的正负号。
引理4.1:当引理3.1中的2次分曲面函数 具体变为定理2.2中的方程(1)~(6)中的二次曲面函数时,共形成36个标准方程。
具体变为定理2.2中的方程(1)~(6)中的二次曲面函数时,共形成36个标准方程。
证明:当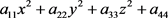 变为
变为 时,由引理3.1有下面6个标准方程:
时,由引理3.1有下面6个标准方程:
(1) ;
;
(2)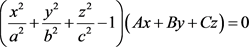 ;
;
(3) ;
;
(4) ;
;
(5)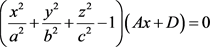 ;
;
(6)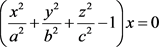 。
。
同理,当 被二次曲面函数(2)
被二次曲面函数(2)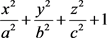 ,(3)
,(3) ,(4)
,(4) ,(5)
,(5) ,(6)
,(6) 依次代替后,我们可以再得到30个标准方程,不妨依次编号为(7)~(36)。 □
依次代替后,我们可以再得到30个标准方程,不妨依次编号为(7)~(36)。 □
引理4.2:当引理3.2中的2次分曲面函数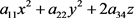 具体变为定理2.2中的方程(7) (8)中的二次曲面函数,或当引理3.3中的2次分曲面函数
具体变为定理2.2中的方程(7) (8)中的二次曲面函数,或当引理3.3中的2次分曲面函数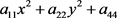 具体变为定理2.2中的方程(9)~(13)的二次曲面函数时,共形成70个标准方程。
具体变为定理2.2中的方程(9)~(13)的二次曲面函数时,共形成70个标准方程。
证明:当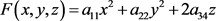 具体变为
具体变为 时,由引理3.2有下面10标准方程:
时,由引理3.2有下面10标准方程:
(37)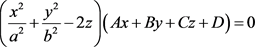 ;
;
(38)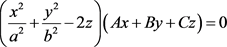 。
。
(39) ;
;
(40) 。
。
(41) ;
;
(42) ;
;
(43) ;
;
(44) ;
;
(45)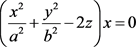 ;
;
(46) 。
。
当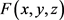 依次被二次曲面函数(8)
依次被二次曲面函数(8) ,(9)
,(9) ,(10)
,(10) ,(11)
,(11) ,(12)
,(12)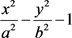 ,(13)
,(13) 代替时,我们可以再得到编号为(47)~(106)共60个标准方程。 □
代替时,我们可以再得到编号为(47)~(106)共60个标准方程。 □
引理4.3:当引理3.4中的2次分曲面函数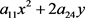 具体变为定理2.2中的(14)时,共形成14个标准方程。
具体变为定理2.2中的(14)时,共形成14个标准方程。
证明:当 具体变为
具体变为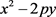 时,由引理3.4有下面14个标准方程:
时,由引理3.4有下面14个标准方程:
(107) ;
;
(108) 。
。
(109) ;
;
(110) ;
;
(111)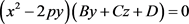 ;
;
(112) ;
;
(113) ;
;
(114)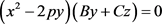 ;
;
(115)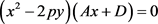 ;
;
(116) ;
;
(117) ;
;
(118)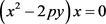 ;
;
(119) ;
;
(120) 。
。
引理4.4:当引理3.5中的2次分曲面函数 具体变为定理2.2中的方程(15)~(17)中的二次分曲面函数时,共形成30个标准方程。
具体变为定理2.2中的方程(15)~(17)中的二次分曲面函数时,共形成30个标准方程。
证明:当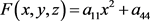 具体变为
具体变为 时,由引理3.5有下面10标准方程:
时,由引理3.5有下面10标准方程:
(121)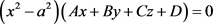 ;
;
(122) 。
。
(123)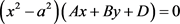 ;
;
(124) ;
;
(125) ;
;
(126) ;
;
(127)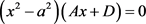 ;
;
(128) ;
;
(129) ;
;
(130) 。
。
当 依次被二次曲面函数(16)
依次被二次曲面函数(16) ,(17)
,(17) 代替时,可以再得到编号为(131)~(150)共20个标准方程。 □
代替时,可以再得到编号为(131)~(150)共20个标准方程。 □
定理4.1:三次复合曲面(4),在适当选取坐标系,并不考虑平面系数的正负号条件下,共有150个标准方程。
证明:由引理4.1得36个标准方程;由引理4.2得70个;由引理4.3得14;由引理4.4得30个;故共有150个标准方程。 □
基金项目
本研究得到云南省高校科技创新团队支持计划资助。