1. 连接算法的要素
相互连接是个体之间的一种运行模式,也是一种很基础的作用模式。在《以接口作为基础的智能模型》 [1] 中把接口连接作为一种智能的基础来探索它可以做的事情和构建的模型。当然一种智能模型也是需要拥有它自己相对应的智能算法的支持。那么接下来就探讨以连接个体相关的智能算法。
首先连接个体之间它们最擅长的行为,是相互之间通过接口或者其它模式(例如磁铁的正负极相互吸引)叠加在一起。如果不加以控制的话,就会以一个点为中心形成一个圈的形状。那么需要探讨的关系除了初始的接口和其它连接模式之外,还需要知道它们形成整体之间是怎么相互作用的。通过一个点形成一个整体,并且拥有整体之间的相互作用的模式,为它们寻找相应的算法就是我们的目标了。
而与这个目标最类似的,就是黏菌的行为了。黏菌是一种生长力比较旺盛的生物,在获得食物点处开始向外生长,并且与不同食物点的黏菌团连接。最后黏菌团缩减成为了不同食物点之间最短路径的线条 [2] 。它拥有着寻找不同点间最短的路径,走迷宫,修复之前的路径成为最短路径的功能。这里就粗略来分析下它拥有修复功能的原因。如下图1所示,假如它一开始拥有并不是最短路径的B0,OA,OC这3段路径。首先假设就只有C1点开始向外生长扩充,并且跟OA连线交与A1点。那么对于C1来说,它到A点和B点的路径为,C1A1A,C1B。小三角形O,A1,C1里面对应着A1C1,C1O与没有连接前的路径OC1,OA1相比较还是要长的。也就是如果只有C1点开始往外扩张,并且尝试修复,那么路径总和并没有减少。而现在从B1点也开始向外生长扩张,与0A交与A1点。那么之前的路径,OB1,OC1,OA1就变成B1A1,C1A1。这2条相加会比3条相加短点,因此它们的路径也就是变成了B1A1,C1A1。那么整体慢慢地做类似于这样的微积分过程,就会形成修复功能,最后成为一个最短路径的整体。
从上面的分析可以得出的结论是:1) 单一点无法完成修复过程;2) 需要从修复点会向外生长扩张的过程;3) 扩张的整体之间可以相互连接。当然整体之间的相互连接,已经有很多算法支持了比如蚁群算法,退火算法等。但这里侧重说明从一点向外扩张的过程在算法上的对应关系。因为它们最终会收缩成为一条线B1A1或者C1A1。那么之前以B1为圆点形成的圆,就类似形成了无数条B1A1线的集合体,而在这个集合体里最终保留一条最短的B1A1。这个过程类似于量子力学里面的叠加状态。可以把以B1点为圆心形成的圆,看成是很多条可能存在线条的叠加状态。最后从这个叠加状态里面选择一个最佳值。因为最后整个圆也会消失的,之前的存在相对于现在的B1A1来说就是一种叠加状态。那么可以说黏菌的修复过程就完成了一个类似于量子叠加,然后再选出最佳的过程。
再回到个体相互连接这里,之前的个体相互连接形成的整体就相当于黏菌形成的整体。然后整体之
间的联系,就可以通过类似于黏菌一样的信息素来选择最短的路径。而其它不需要的连接就可以去除掉。这样就形成了需要的最短的连接。那么相互连接的算法也就找到了。在这里把它们从一个点相互连接形成一个整体的过程,叫做形成叠加状态的整体。叠加状态之间选择的参数,叫做连接参数。那么连接要素点可以概括为:1) 相互连接形成一个叠加状态的整体。2) 通过连接参数选择最优的连接。
当然上面提到了一个“信息量子化”的假设,这里说明下怎么做的。量子我们知道是一种同时拥有多种状态的个体,类似于每个个体处在平行世界一样。而我们生活中的事物,信息几乎都是不存在这种状态的。也就是几乎不存在同一时间多种状态的个体,但如果是不同一时间,甚至是多个个体组成的整体,可以形成一种相对关系的,类似于单个量子个体的效果。举例说明下,比如统计你100天做的事情,那么这100天做的事情,对于你来说就是你个人的可能做事情的状态。但因为时间是单向的,并没有办法让你同时处在每个事情的状态里。而现在用100个你的克隆人分别处在这100种事情的状态里。那么这100个克隆人相对于你来说,就形成了一种类似于量子的不同世界的叠加态的效果。假如要你在某个地方跟某个人碰面,这100个克隆人里面,会存在一个最近的人到达碰面的地点。最后全部克隆人都消失了,你直接变成了那个最近的克隆人。这100个克隆人,对于任何一个克隆人来说都是不存在多个状态的,但是他们整体相对于你来说,是一种相对关系的叠加状态。上面的黏菌也是类似于这样的效果,得到食物点的黏菌开始繁殖。然后繁殖的整体,相对于当初的黏菌来说是一种叠级状态。这个整体中的任何个体,也都可以进行相互联系,繁殖等功能。并且最后,整体缩减成为了最短距离路径的个体连接。
接口的连接也可以看成是这种关系。比如两个积木块要相互连接,并且它们分别可以跟其它的积木块连接。那么积木块跟其它积木块连接形成的整体,相对于当初的两个积木块来说,是一种叠加状态。然后两个积木块形成的整体,就可以挑选最合适的连接桥梁,从而形成最初两个积木块最合适的连接方式。对于信息来说,信息之间通过某个连接关系和计算方法获得的信息整体。并且也给这个信息整体里的每个信息也进行连接关系和计算方法的运算。通俗一点来说就是,给这个信息做运算,并且每个不同信息结果也都可以继续进行运算。那么这个信息整体可以看成是信息相对于某个连接关系和计算方法形成的叠加状态。也就是信息并没有被量子化,而是随着连接和计算,形成了一种相对关系的“量子化”。
2. 不同连接参数例子和说明
从上面可以直到执行连接算法的关键就是获取叠加状态整体和连接参数了。叠加状态通过上面的分析,可以是从起始点个体尽可能地连接其它个体来获取叠加状态,甚至是重复多次地从起始点开始连接,只要获取多次里面不重复的连接作为整体的叠加状态。而连接参数则是设定好的一些传递参数。例如黏菌的信息素,随着路程减少,还有食物点的信息素等。那么下面就列举几种不同连接参数下的连接智能算法。
2.1. 连接参数是递减或递增的关系
这种比较典型的就是黏菌和蚂蚁的信息素,会随着距离而减少,重复多次的地方信息素相对较高。较高信息素的路径就会变成整体最短的路径。如下图2所示,制作一个10 * 10的小方框,然后设置食物点[3,6],[6,0],[9,10]。

Figure 2. Calculating the shortest distance
图2. 计算最短距离
设置传递参数(信息素)初始值为10,并且随着距离增加1,则减少1。那么随着连接参数的扩散,最终会形成图中红色线条所示的路径,也就是3点之间最短的路径和。当然这些都是已知的,也被用到寻找城市间最短的道路设计,物流路线设计等的作用上。从叠加状态和连接参数的角度上分析就是,叠加状态是从3个点出发,不同的位置点之间的连接。比如[9,10]点跟[9,9],[8,10],[10,10] 3个点连接。而最后这些连接的点都会消失,只保留连接参数最大的红线的哪些点。其它的点也只是曾经存在的状态,最后并不会保留。
2.2. 连接参数是合成的关系
连接参数是合成的关系,这种类似于力的传递。任何一个形成的地方都要能够承受这种力的作用。例子如:通过不同的承受力的模块和数量不等的接口块,形成一个连接整体。可以支持(X:0, Y:5)起始点−40 N力的输入和(X:10, Y:5)终点40 N力的输出 [3] 。那么它们最终形成的是如下图3所示,每个地方都是支持起始点的终点的正负的40 N的拉力。它们的整体就能够适应这种拉力的最短的连接模式。这种连接参数是合成的模式,可以形成类似于人体的骨骼,肌肉等的形状。也可以做一些建筑模型上面,承受力的骨架构建。这里的叠加状态就是从起点和终点开始,形成不同接口块的组合。最后会停留在适应合成连接参数的最小的整体。其它的连接块消失后,就形成图中最小的整体。这个看起来不太智能,但是如果连接的数量多到像肌肉细胞一样多,那么还是需要这种自动形成的模式来构建复杂的整体。在自然中包括动植物的各种外表,形状等都可以形成,并且是从最小的连接块开始构建形成。

Figure 3. Schematic diagram of individual connections
图3. 个体连接示意图
2.3. 连接参数是某个值
两个叠加状态之间,连接的值是相等值,可见于量子计算机模式。量子计算机的计算模式同时拥有着1,−1的叠加态。如图4所示,并且最后通过选择停留在最佳的状态上。它的连接参数是一些权值。权值分别乘以两边的叠加状态。也就是1,−1是形成的叠加状态,然后连接参数就是它们之间的权值。(由于我并不懂量子计算机,只是看原理有些类似,就不继续讨论了。)它在实际中的例子,比如动物寻找到食物,就发出信号来叫伙伴过来,如果它们找到水了,会发出另外一种信号,遇到危险了又是另外中信号。可以说连接参数是某个值的,是最简单的连接参数了。

Figure 4. The most basic operation of a quantum computer is to support the energy program
图4. 量子计算机最基础的操作就是支持能量程序
2.4. 连接参数是相反的两个值
这种情况下类似于接口的扩展。本来两个可以直接相互连接的接口个体分开了,但通过相连接的连接个体把接口信息传递过去。从而到达即使两个物体相隔很远,也可以相互连接的效果。实际生活中类似于磁铁的正负两级,电流的正负电子等。它们通过介质,即使相隔很远也可以相互连接。而叠加状态就是在介质中的扩散模式,连接参数就是正反的两个值。在接口连接中叠加状态可以通过更多的个体相互连接形成,而正负的传递参数可以确保这两个叠加状态进行连接。下面用例子简单说明下正反连接参数的应用。
例子:拥有2组起始数据[5,10,15,20],[2,2,2,2],拥有起始点的可拼接计算方法,加1,加2,相加,相乘和目标点的可拼接计算方法减1,减2。并且用这些方法组成到目标数据[145,165,185,205]的方法整体。
那么在这里把2个起始数据设置为正的连接参数[interface,34234],把目标数据设置为负的连接参数[-interface,34234]。并且从起始数据开始用数值增加的计算方法作运算,而对目标的数据作数值减少的计算方法运算。达到扩大它们的两者的叠加状态。只要目标点的叠加状态的值,跟起始两个点的叠加状态的值相重合了,那么连接就算完成了。如果下图5所示:
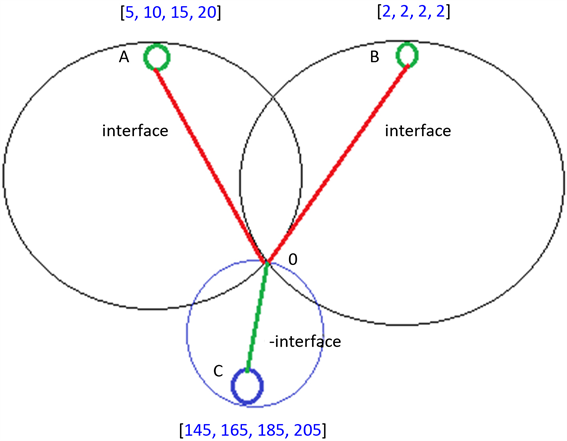
Figure 5. Positive and negative connection parameters
图5. 正反的连接参数
在它们拥有相互重叠的值后,就停止了A,B,C这3点的计算法方法拼接。然后从O点开始,作OC连接方法的相反的方法,也就是减1变成加1,减2变成加2。这样就可以得出起始数据到达目标数据的方法整体。当然这里为了方便计算,使用了同时拥有正负方法的,加1,减1,加2,减2。不拥有相反的计算方法的话也是可以的,只要沿着OC每次拼接2个相邻点间最短的算法组合就可以了。相当于拥有路标一样地指导着形成。如果是按照正常方法拼接的话,会是一个比较庞大的计算量。当然这样形成的结果只是保证了3点之间方法的连接,它们的方法组合可能并不是最优的方法组合。那么只要再用上面的递减的连接参数对它进行优化,就可以到达最短的方法组合。
同时拥有正反连接参数的模式的优点有下面几点,1) 可以保证多个点之间相互对应关系,减少了不相关点之间相互影响的情况。2) 很大程度上加强了连接的可能性。比如目标是一个复杂的整体,那么就可以通过分解的方法慢慢分解成为小部件。起始的组合整体,只要跟这些小部件匹配上,再进行反向的组合,就可以形成复杂的整体了。如果目标个体是很小的个体的话,也可以通过连接扩展把连接目标变大,从而方便进行连接。
3. 连接智能模式的形成
从上面的不同连接参数和形成的叠加态整体可以看出。如果把形成的点提取作起始点和目标点,那么就可以实现循环调整的功能。这种循环会一直持续,直到这个整体达到设定目标的最优值。这个过程为:对起始点和目标点进行叠加状态的扩展→连接参数选择合适的连接组合→从连接组合里面选取新的起始点和目标点→进行新的扩展和选择……那么这样的话一个智能模式就形成了。用上面例子作分析,先通过正反的连接参数找到[5,10,15,20],[2,2,2,2]两组数据到[145,165,185,205]目标数据的连接。然后对这个连接进行连接参数递减的连接处理。如果拥有更加复杂的对应关系,可以把目标数据先做分解向的处理。之后分解的小块依次跟起始数据形成新的正反连接参数的连接,如果还不行就继续分解,直到它们全部都连接在一起 [4] 。那么这样的话,可以想象即使一个很复杂的物体也是可以通过连接智能模式来连接完成的。比如你要建造一栋房子或者一台机器,连接智能模式就可以控制部件单元形成它们的最佳模式。
4. 总结
连接智能算法可以通过连接单元进行连接扩展,形成类似于叠加状态的整体。之后再通过不同的连接参数对这些整体进行筛选,获得目标的个体连接模式。连接的模式还可以通过继续形成新的连接个体,来达到循环的连接和选择模式。循环的连接智能算法可以一直调整,直到选出最优的目标连接模式。可以应用到目标函数的拼接,建造模型的构建,物质的分解和形成这些方面。