1. 问题背景
2003年Malmborg教授及其课题组首先提出自动小车存取系统,它主要包括轨道导引小车系统,通过RGVS小车进行货物存取。RGVS控制系统通常与AGVS比较,RGVS智能加工系统优化调度一直是研究的热点。目前众多国内学者对此做出了许多研究,罗键 [1] 等初步概述了智能加工系统调度的一般方法。刘丰瑞 [2] 等用动态规划法建立最优路径的逆序递归数学模型,求解复合作业的最佳配对组合,使复合作业的路径优化方法更加简单。张甜宗 [3] ,陈粱 [4] 等通过遗传算法时利用多重编码技术,结合计算机模型仿真求解进行研究。刘二辉 [5] 等提出一种用于求解复杂环境下自动导引小车路径规划问题的改进灰狼优化算法,引入路径微调算子和邻域变异算子来提高灰狼优化算法的局部开发能力,采用改进的路径片段与障碍物相交判断算法来提高算法的运行效率。江唯 [6] 等以任务最短完成时间为目标,此基础上提出路径最短和堵塞次数最少两个优化目标,提出了改进的自适应权重的求解方案,进一步提高了算法性能。智能算法的缺点在于收敛速度较慢以及求解时容易陷入局部最优,因此解决算法获得最终较优解的时间效率问题成为未来研究的重点 [7] [8] ,这也是智能算法在实际生产过程中的瓶颈问题。
图1是一个RGV有轨制导车辆系统,是集各高新技术于一体的系统,配合CNC计算机数控机床在物料加工方面有一定的实际应用。它有一个机械手臂、两只机械手爪和物料清洗槽,能够完成上下料及清洗物料等作业任务。本文讨论的是在结合8台CNC、1条RGV直线轨道、1条上料传送带、1条下料传送带等附属设备条件下,如何实现物料加工的效率最高化问题。
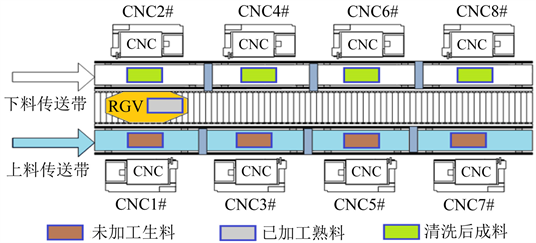
Figure 1. Schematic diagram of intelligent machining system
图1. 智能加工系统示意图
图1中的工作分为执行移动、停止等待、上下料和清洗作业四个部分且这四个部分只能独立作业并且需要耗费一定时间,CNC同一时间只能安装1种刀具加工1个物料,本文针对不同情况解决动态调度的最优模型问题并求出相应的算法。同时也提供一些数值计算实例,检验模型的实用性和算法的有效性,并且给出具体的调度策略以及系统工作效率。
2. 模型的假设
为讨论方便,不失一般性,假设如下:
(一) 假设给定的上下料时间为单次上料或单次下料的时间。
(二) 假设上下料传送带运行过程不发生事故。
(三) 假设不发生RGV中途断电、失联、死机等突发状况。
(四) 假设生料传送到CNC后传送带马上运输新的生料。
(五) 假设RGV没有收到指令时自动向最快将要结束作业的CNC移动。
物料加工效率受RGV的移动时间、给CNC上下料时间、停止等待时间、清洗作业时间、CNC加工时间五个主要因素的影响(该五种因素相互独立),由于清洗工作时间、CNC加工时间是一定的,所以可以将其视为两个固定不变的量,本文主要考虑剩下的三种因素,问题描述如下:
1) 通常认为,RGV的移动时间越少越好。因此,我们采取就近原则。基于最近站点优先规则,即RGV离哪台CNC近,就将生料给哪台CNC上下料,当CNC加工好后,给 发出信号,同样的, 离哪台CNC近就去哪台,如果出现两台同样距离的CNC向RGV发出信号,再由具体计算决定
2) RGV的上下料时间偏短为好。8台CNC平均分布在RGV两侧,设RGV编号为奇数的一边(1, 3, 5, 7)为A组,编号为偶数(2, 4, 6, 8)的一边为B组。B组所花费的上下料时间要大于A组所花费的上下料时间。所以在RGV两侧都有CNC时,应先给A组上下物料。
3) RGV的停止等待时间越短越好,当所有CNC都在工作时, 自行进行移动至最快完成工作的CNC出进行等待。
4) 当物料加工需要两道工序时,在一道工序的基础上,物料需要经过不同的CNC进行二次加工,这时CNC不同刀具的分配将会影响RGV的调度模型。
3. 模型建立与数值计算
3.1. 一道工序动态调度仿真模型
由于一台RGV在同一时间只能为一台CNC上下物料,并且RGV运动需要花费一定时间,因此为了在特定时间内可以加工最多的物料,本文让RGV尽量节省移动耗费的时间,让RGV以就近原则为基础,模拟仿真整个智能加工系统作业过程。一般情况下,每一台CNC的工作状态可采用0~1变量表示,以CNC是否向RGV发送信号为决策变量进行0~1规划,
,具体如下:
(1)
其中,0表示CNC正在加工,1表示CNC处于等待加工状态,
表示第
台CNC。将智能加工系统分为4列,定义第
个CNC所处的列数
,具体计算公式如下:
(2)
同时,定义RGV当前所在的列数
。以此,我们可以计算RGV到任意CNC的单位距离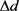 ,
即是RGV将要移动的距离(相邻两列的距离为一个单位),计算公式如下:
,
即是RGV将要移动的距离(相邻两列的距离为一个单位),计算公式如下:
(3)
RGV为偶数编号CNC一次上下料所需时间要大于为奇数编号CNC一次上下料所需时间,并且为了尽快地开始进行上下料工作,因此,RGV选取下一次上下料所在的CNC的规则如下:CNC的当前状态处在等待加工即
。此CNC与RGV的距离为最短距离
。在
相等的情况下优先选择奇数编号的CNC。在智能加工系统中,作业时间T中包括RGV移动的时间
,RGV停止等待的时间
,RGV为CNC一次上下料的时间
,CNC加工完成一个一道工序的物料所需时间
,RGV完成一个物料的清洗作业所需时间
。以RGV为观察对象,另外,引进变量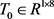 为包含各CNC加工完成的时刻。定义一般班次的时间
为包含各CNC加工完成的时刻。定义一般班次的时间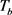 在系统工作时间
内,得到作业时间T计算公式如下:
在系统工作时间
内,得到作业时间T计算公式如下:
(4)
最后,我们还确定了一个对RGV移动的指令如下,在
的时候,RGV前往最快使生料成为熟料的CNC去。
综合上述分析可知,智能RGV的动态调度策略是为了让智能加工系统在某班次时间内达到成料数最大化,因此以成料数最大化为目标,得到智能RGV动态调度模型目标函数:
(5)
其中,
为第i个RGV的成料数。以式(5)为目标函数的模拟仿真模拟,利用下表1系统作业参数的3组数据分别检验上述模型的实用性和算法的有效性,得到关于智能RGV加工系统的作业效率。

Table 1. Three sets of data tables of operation parameters of intelligent machining system
表1. 智能加工系统作业参数的3组数据表
对于只有一台RGV的智能加工系统,以RGV为观察对象,定义一个班次中RGV的作业效率
,具体计算公式如下:
(6)
其中,
为给定一个班次的时间,
为RGV等待时间。
对于有八台CNC的智能加工系统,以CNC为观察对象,定义了一个班次中八台CNC的平均作业效率
,具体计算公式如下:
(7)
其中
第
个CNC班次中总的等待加工时间。
利用MATLAB设计程序,分别代入表1三组数据,得到一个班次8小时的成料数最大化,并分别计算出RGV,CNC的工作效率
如表2:
系统的总作业效率主要分为RGV,CNC的工作效率
两部分,由上述表中可以看到:对于表1智能加工系统作业参数的3组数据表可知,第一组数据和第三组数无论是加工时长,上下料时间,RGV移动时间还是物料清洗时间相差不大,所以得到的实际成料数相差甚微;观察第二组实验数据可知,RGV小车移动时间,物料加工时长,上下料时间以及清洗时间都比其他两组数据明显耗时,因此第二组数据得到的成料数明显低于其他两组。从系统工作效率来看,三组数据工作效率较高且波动不大,从而可知该模型的算法可行、可操作。
3.2. 二道工序动态调度模拟仿真模型
两道工序加工物料时,生料需要先后经过两台分别装有两种不同刀具的CNC才可以加工完成。每台CNC只能完成其中一道工序,因此,我们以可以完成最大数量的生料加工为目标函数,用0-1规划模型求解最佳CNC的两种刀具分配以及RGV的调度。
定义安装不同的刀具的CNC,其中完成第一道工序的CNC集合为
为安装第一种刀具的CNC的台数;完成第二道工序的CNC集合为
为安装第二种刀具的CNC的台数。
在两道工序的加工系统中,未在上下料时,RGV机械手爪的状态分为两种包括:1) 手中没有料子;2) 手爪中抓有被第一道工序加工完成的。
因此RGV需要判断自身机械手爪状态来选择下一道工序,因此可采用0~1变量表示,以RGV的机械手爪实时状态为决策变量进行0~1规划,具体如下:
(8)
其中,
表示下一道工序去
类,
表示下一道工序去
类。
一道工序的智能加工系统不同,两道工序的智能加工系统作业时间
中还包括CNC加工第二道工序的物料所需时间
。所以,两道工序智能加工系统得调度策略会因安装不同种刀具的CNC的台数而不同。因此,为了让智能加工系统在某班次时间内达到成料数最大化,同样以成料数最大化为目标,让CNC安装不同的刀具的情况为决策变量,规划最优的CNC刀具分配。
在上述基础上,运用蒙特卡洛算法思想模拟仿真,随机产生出CNC的刀具分配情况,寻找出成料数最多的CNC刀具分配方案。
通过MATLAB设计程序,分别代入表1三组数据,得到一个班次内多种成料数最大值的CNC刀具分配方案(见表3)。选取了RGV,CNC的工作效率
最高的一组数据,得到了基于这种数据RGV的调度策略。
对上述结果进行分析:与表一给出的3组数据表结合分析可知,在第一道工序和第二道工序所消耗的时间上,第一组数据CNC加工两道工序所需时间几乎相等,因此,求得两道工序都是3台轮换,符合实际情况;第二组数据CNC加工第二道工序所需时间远远大于第一道工序,因此分配给第二道工序的CNC应当大于第一道工序的CNC,实验结果显示第二道工序的轮换是4台,而第一道工序轮换是2台,符合实际情况。第三组数据CNC加工第一道工序所需时远远大于第二道工序,因此分配给第二道工序的CNC应当大于第一道工序的CNC,实验结果显示:第一道工序的轮换是4台,而第二道工序轮换是2台,符合实际情况。
综上所得,在多道工序并存的动态调度策略中,CNC的分配与各工序作业时间的关系密不可分,基于本文的背景,耗时长的工序应当分配更多的CNC进行轮换,由此可见,模型得出的调度策略非常符合实际情况。
4. 结束语
为了解决原有的智能算法得到最终较优解的时间较长以及旧型动态算法鲁棒性较差的弊端,在原有基础上提高系统的运行效率,本文通过RGVS的存取方式,建立RGVS动态调度策略模型,在此基础上探讨RGVS出入库问题的方法,以一定时段区间内智能加工系统的成料数为目标,同时引入智能加工系统中不同设备的工作效率的概念,针对指定的问题背景与实际数据,通过本文建立的算法模型在计算机进行仿真模拟,得到基于问题背景的可靠实验数据,为研究者提供与老旧方法不同的可行的思路和可靠的研究方法。
基金项目
湖南农业大学校科学基金项目17QN19带注资策略的离散时间模型的最优红利问题。
NOTES
*通讯作者。